隐私计算编年史：重构信任的密码学征途

当人工智能越过图灵门槛，区块链重构信任结构，数据本身正悄然取代能源，成为新一轮文明跃迁的核心资源。然而，在这场浩大的科技进程中，我们才刚刚意识到一个古老的问题正在卷土重来： 人类是否还能拥有真正的隐私？

The greatest enemy of knowledge is not ignorance, it is the illusion of knowledge. ——Stephen Hawking

隐私计算（Privacy Computing）由此而生。它不是某项孤立技术的突变，而是密码学、分布式系统、人工智能与人类价值观之间长期博弈的结果。自 20 世纪末期多方安全计算、同态加密等理论框架提出以来，隐私计算逐渐演化为应对“数据失控”时代的关键护栏——它让我们在不暴露原始数据的前提下，仍能合作计算、共享价值、重建信任。

这是一段仍在发生的技术史，更是一场关于“自由意志能否在算法世界存活”的哲学提问。而隐私计算，也许正是通往答案的第一扇门。

一、萌芽期（1949 年– 1982 年）：现代密码学的起点

1949 年：香农与信息论的开端

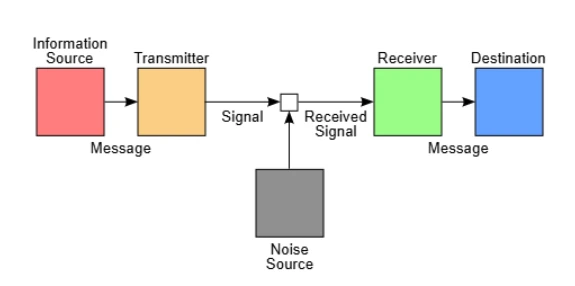
1949 年，克劳德·香农在论文《保密系统的通信理论》中首次以严格的数学方法系统地分析了通信系统的安全性。他利用信息论方法定义了“完善保密性”，指出只有一次性密码本（one-time pad）能够满足这种严格意义上的安全需求。香农的研究方法极其严谨，从数学原理出发，运用概率论和统计学方法建立保密系统模型。他明确了熵和信息量的概念，奠定了现代密码学的理论基础。

香农在其 1948 年论文《通信的数学理论》中提出的经典通信模型，展示了信息源、编码器、信道、解码器和信息接收者之间的关系

香农的研究过程富有创造性，他在贝尔实验室工作期间，不仅致力于理论研究，也进行大量的实验验证。他习惯用直观的类比来解释复杂概念，例如将信息传输类比成水流、熵类比成不确定性。据趣闻所载，他还曾在实验室走廊骑独轮车来放松和激发创造力。这篇论文的影响深远，不仅奠定了现代密码学的理论基础，也影响了后续几十年间整个信息安全领域的研究路径。

1976 年：Diffie-Hellman 的突破

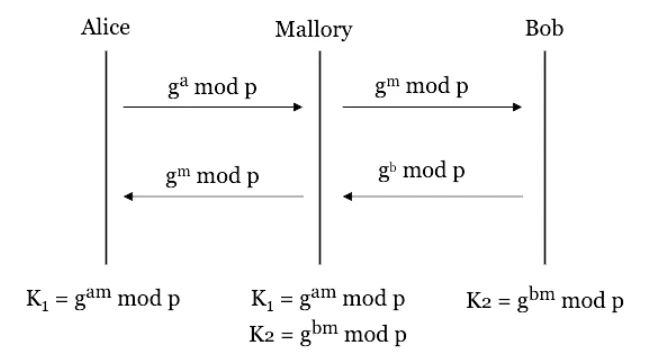
1976 年，Whitfield Diffie 和 Martin Hellman 在《密码学新方向》一文中提出了公钥加密的概念，设计了 Diffie-Hellman 密钥交换协议。这一协议的研究方法基于离散对数问题的数学难题，两人首次提出了无需预共享秘密即可安全交换密钥的方案。

该图展示了 Diffie-Hellman 密钥交换的基本流程，Alice 和 Bob 通过公开的信道交换信息，最终生成共享的密钥，而不被窃听者得知

研究过程并非一帆风顺，两人花费了多年时间不断尝试和失败，在深入研究数学和数论基础上，最终才找到适合的数学构造。Diffie 因为其与众不同的外形和行事风格，在学术界也引起了不少趣闻轶事，比如会议组织者经常误将他认作摇滚乐队成员。这项工作从根本上改变了密码学领域，为数字签名和其他现代安全协议奠定了基础。

1977 年： RSA 算法诞生

1977 年，麻省理工学院的 Ron Rivest、Adi Shamir 和 Leonard Adleman 联合发明了著名的 RSA 算法，这是首个实用的非对称加密算法。他们的研究方法采用了大素数因子分解问题作为安全基础，通过复杂的数学推导和计算机实验成功构造出实用的非对称加密机制。

该图展示了 RSA 加密和解密的过程，包括公钥和私钥的生成，以及如何使用公钥加密和私钥解密信息

研究过程中，Rivest 最初在经历了一整夜的尝试后突发灵感，迅速完成算法草稿；而 Adleman 则负责了算法实现和验证。他们用 RSA 算法加密了一条著名的消息，挑战同事解密，以此纪念这个重要时刻。RSA 算法不仅具有理论意义，更重要的是为电子商务、数字签名等应用场景提供了实际的安全方案。

1978 年：同态加密的雏形

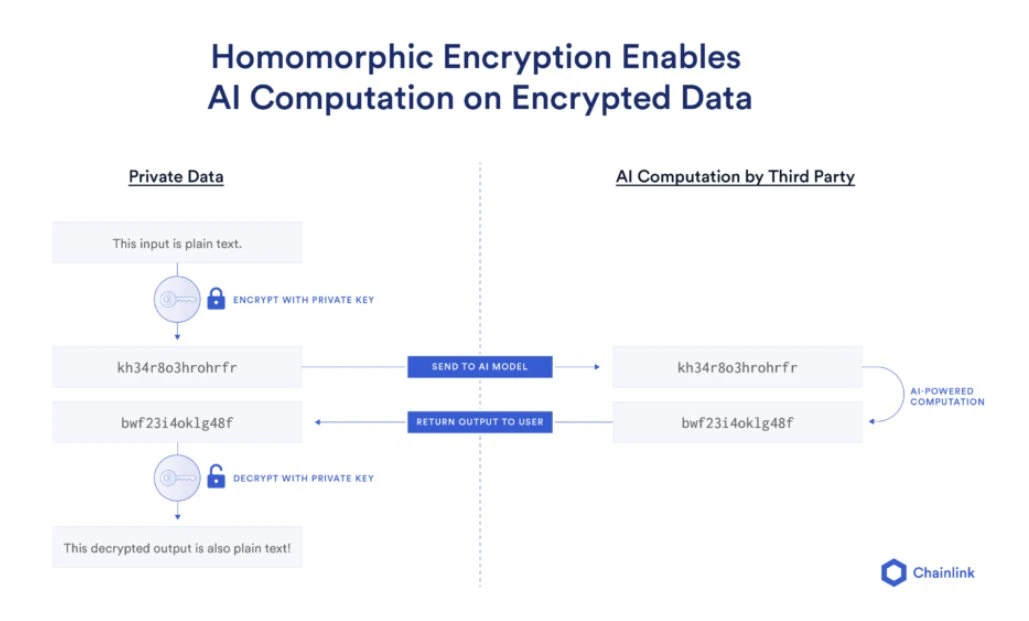
1978 年，Rivest、Shamir 和 Adleman 在提出 RSA 算法后，又在探索加密数据的计算可能性，即同态加密的概念。他们提出问题时，只简单指出一个加密系统能否允许密文直接进行运算而无需解密。虽然当时未能解决这一难题，但他们提出的这一前瞻性问题，却引发了未来三十多年密码学界的持续探索。

该图展示了同态加密的概念，即在密文上直接进行运算，解密后得到的结果与在明文上运算的结果一致

1979 年– 1982 年：密码学百花齐放

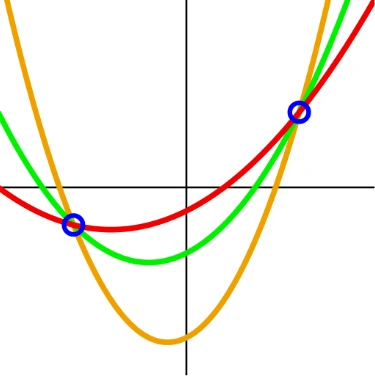
在此期间，密码学领域迎来了诸多开创性的理论研究成果。Adi Shamir 提出了秘密分享方法，通过精妙的代数结构设计，使秘密信息被多方安全管理，并且只有在特定数量的人参与时才可以重构秘密。

通过 2 个点可以绘制无数个 2 次多项式。需要 3 个点才能唯一确定一个 2 次多项式。此图仅供参考——Shamir 的方案使用有限域上的多项式，这在二维平面上不易表示

Michael Rabin 在研究中提出了不经意传输（Oblivious Transfer），这种协议巧妙解决了信息交换中双方的信任问题，使得一方能够安全地获取信息而对方却无法知晓具体内容。

姚期智在 1982 年提出了著名的“百万富翁问题”，以诙谐而形象的方式，将复杂的密码学思想直观展示出来，描述如何在不暴露各自财富具体信息的情况下安全地确定谁更富有。姚期智的研究方法使用了抽象的逻辑推导和博弈论方法，这项研究直接启发了后续安全多方计算（MPC）的研究热潮，推动了密码学在信息共享、数据隐私保护等领域的广泛应用。

这些丰富而深入的研究成果共同推动了现代密码学领域的初步繁荣，为未来的技术演进奠定了坚实的基础。

二、探索期（1983 年– 1999 年）：理论爆发与隐私工具雏形

1985 年：零知识证明的诞生

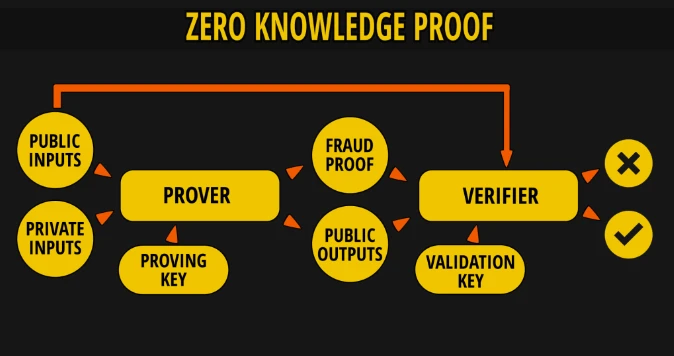
1985 年，麻省理工学院的 Shafi Goldwasser、Silvio Micali 和 Charles Rackoff 提出了零知识证明（Zero-Knowledge Proof，ZKP）的概念。他们在研究交互式证明系统的基础上，提出了这样一个问题：如何证明自己知道某个秘密而不泄露这个秘密本身。他们运用复杂的交互协议和概率论方法，设计出证明过程，让验证方能够相信提供证明的人确实掌握某个信息，但同时又无法推断出具体的信息细节。

该图展示了零知识证明的基本流程，证明者（Prover）向验证者（Verifier）证明其拥有某个秘密信息，但在此过程中不泄露该信息本身

趣闻轶事是，这项研究的灵感最初来源于一种简单的纸牌游戏，他们在一次学术会议上以互动游戏的方式演示了零知识证明，让现场观众既感到惊奇又颇为困惑。ZKP 的提出，不仅为现代密码学领域提供了重要理论工具，更是奠定了隐私计算中的重要技术支撑，对后续诸如匿名验证、隐私保护、区块链等领域产生了深远影响。

1986 – 1987 年：安全多方计算的突破

1986 年，姚期智教授提出了混淆电路（Garbled Circuit）技术，巧妙地实现了两方安全计算的协议。他将函数计算转换成复杂电路，再将电路混淆后交由另一方执行，确保对方能计算出结果但无法窥视具体输入数据。姚期智的研究方法将密码学与计算复杂性理论融合，被视为计算机科学的一次突破。

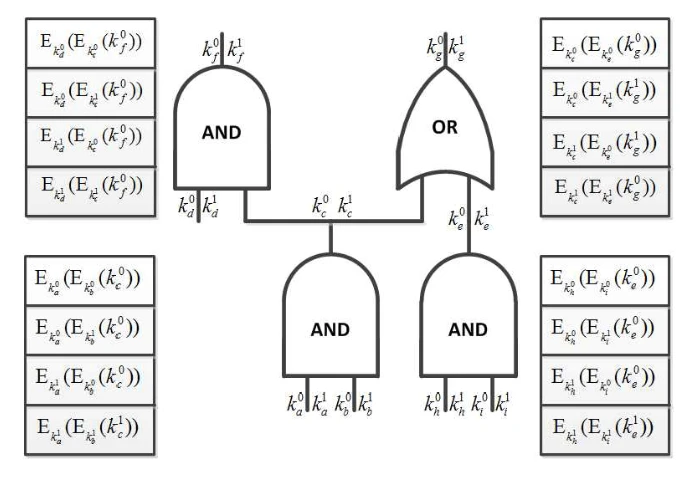
该图展示了姚期智提出的混淆电路（Garbled Circuit）技术的基本结构，演示了如何通过电路混淆实现两方安全计算

趣闻是姚期智独特的跨学科背景让他经常以意想不到的角度切入问题，被学界戏称为密码学界的“黑魔法”。紧随其后， 1987 年，Oded Goldreich、Silvio Micali 和 Avi Wigderson 提出了著名的 GMW 协议，将安全多方计算（MPC）扩展到多方场景，实现多个参与方在不暴露各自输入数据情况下安全执行计算。这些成果实质性地推动了安全多方计算的理论和实际发展，使得隐私计算逐步从理论走向可能。

1996 年：联邦学习的早期设想

1996 年，David W. Cheung 提出了用于分布式系统中的关联规则挖掘算法，虽然当时并未明确提出联邦学习这一术语，但他研究的核心思想与后来流行的联邦学习思想不谋而合。他提出的分布式数据挖掘方法，不要求将所有数据集中在一起，而是让多个独立的数据拥有者各自处理数据并交换挖掘结果。

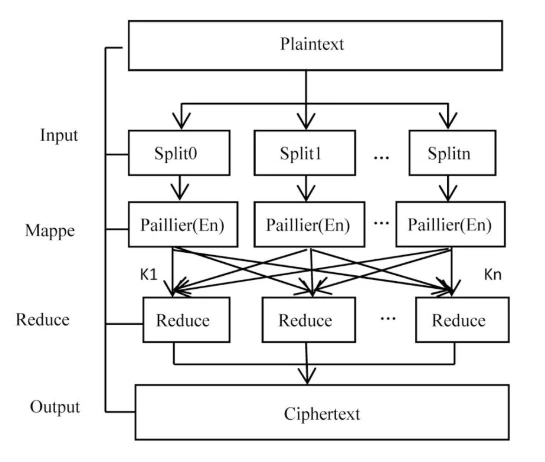
该图展示了 Paillier 加密方案的并行加密过程，说明了如何在密文状态下进行加法运算

Cheung 的研究过程也颇为有趣，他最初是为了解决大型企业内部数据挖掘的难题，却无意中为未来的联邦学习提供了理论原型。当时他的研究并未引起广泛关注，直到 20 多年后，随着隐私问题日益凸显，Google 等公司开始大规模采用联邦学习，这项成果才真正展现出其前瞻性。

1999 年：加法同态加密的实用化

1999 年，Pascal Paillier 提出了一种新的加法同态公钥加密方案，允许密文直接进行加法运算而无需解密。这一研究解决了长期以来同态加密领域的实际应用瓶颈。他采用基于群论的数学构造，实现了安全的加法同态属性，使得数据在密文状态下仍能有效处理，显著推动了加密数据应用场景的实际落地。

Paillier 方案被广泛应用于电子投票、隐私保护数据分析等实际场景。据悉，Paillier 在设计该方案时最初的灵感来源于解决匿名电子投票中的隐私问题，这种需求驱动的研究方法，不仅具有理论意义，也极大促进了同态加密技术的产业化发展。

这一阶段，密码学理论大放异彩，各种新颖的技术与方法不断涌现，为隐私计算的蓬勃发展奠定了坚实基础，也为日后的技术应用提供了丰富的工具与方法。

三、成长期（2000 年– 2018 年）：隐私计算框架成型

2006 年：差分隐私的开创

2006 年，微软研究院的 Cynthia Dwork 提出了差分隐私（Differential Privacy）理论，这一创新理论为大数据时代的数据隐私保护提供了严格的数学保障。Dwork 的研究方法巧妙地利用随机噪声加入数据查询结果，使得单一数据记录的加入或删除对整体查询结果的影响降到极低，从而有效保护了个体数据的隐私。

该图展示了差分隐私的基本机制，通过在查询结果中加入随机噪声，保护个体数据的隐私

有趣的是，Dwork 在早期推广差分隐私时，曾用一本电话簿作为例子来生动地说明隐私泄露的现实风险。她指出，尽管匿名化处理后的数据看似安全，但结合外部信息仍可能恢复敏感隐私。她的研究开创了数据隐私保护的新标准，被广泛用于医疗数据、人口统计、社会科学研究等领域，深刻地影响了后续隐私计算技术的发展路径。

2009 年：全同态加密与可信执行环境（TEE）的突破

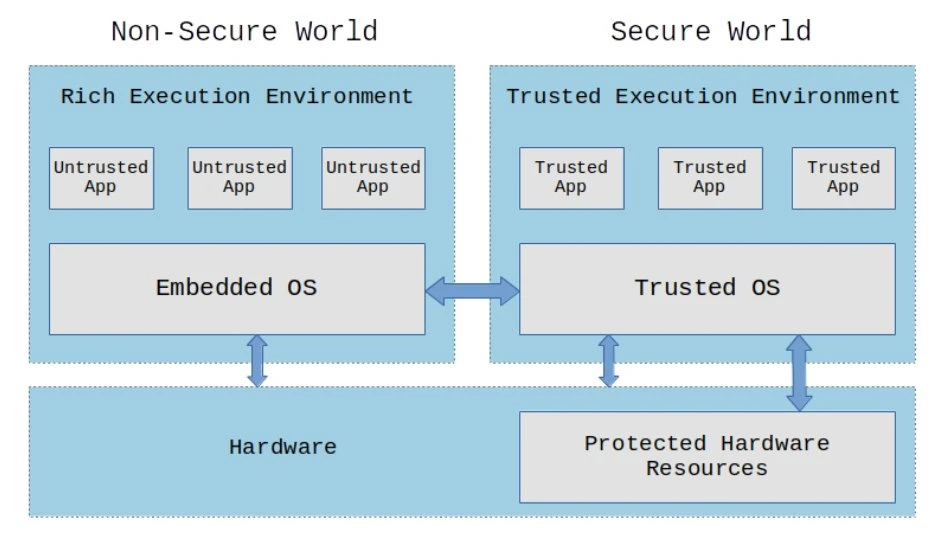
2009 年是密码学技术发展的关键一年。首先，开放移动终端平台（OMTP）首次提出了可信执行环境（TEE）的前身方案，试图在硬件层面上构建隔离安全环境，保护移动设备敏感数据的安全性。

该图展示了 TEE 的基本架构，说明了如何在硬件层面上创建隔离的执行环境，保护敏感数据的安全

同年，IBM 的 Craig Gentry 提出了首个全同态加密（Fully Homomorphic Encryption, FHE）方案。这一理论允许数据在加密状态下进行任意计算，无需解密即可获得处理结果。Gentry 的研究极富传奇色彩，据传他在多年研究陷入瓶颈后，某次偶然的散步中灵光乍现，最终攻克了困扰学界数十年的难题。他的突破开启了密文计算的新篇章，使加密数据在云计算、金融数据分析等场景得到了安全高效的应用。

该图展示了全同态加密的工作流程，说明了如何在密文状态下进行任意计算，并在解密后获得正确结果

2013 年：医疗联邦学习的先驱

2013 年，王爽教授团队在隐私计算领域率先提出医疗联邦学习系统 EXPLORER，这是首次在分布式医疗数据上实现安全模型训练的实践。团队采用分布式机器学习与隐私保护技术相结合的方式，设计出能跨机构合作而无需共享原始数据的模型训练方法。

据报道，这项研究最初动机源于实际医疗研究中的数据共享困难问题，团队在研究过程中历经了多次技术迭代和跨学科合作，最终成功搭建了能够安全共享医疗数据而不泄露患者隐私的技术框架。EXPLORER 系统迅速成为国际医疗数据安全保护的标杆，推动了全球医疗数据协作的新实践。

2015 年– 2016 年：隐私计算产业化的标志

2015 年至 2016 年，隐私计算迎来了产业化的里程碑。Intel 公司发布了首个商业化的可信执行环境技术 SGX（Software Guard Extensions），该技术允许应用程序在硬件层面进行隔离执行，确保敏感数据和程序的安全性。这一突破使隐私保护真正走入实际应用场景，例如安全云计算、金融交易等领域。

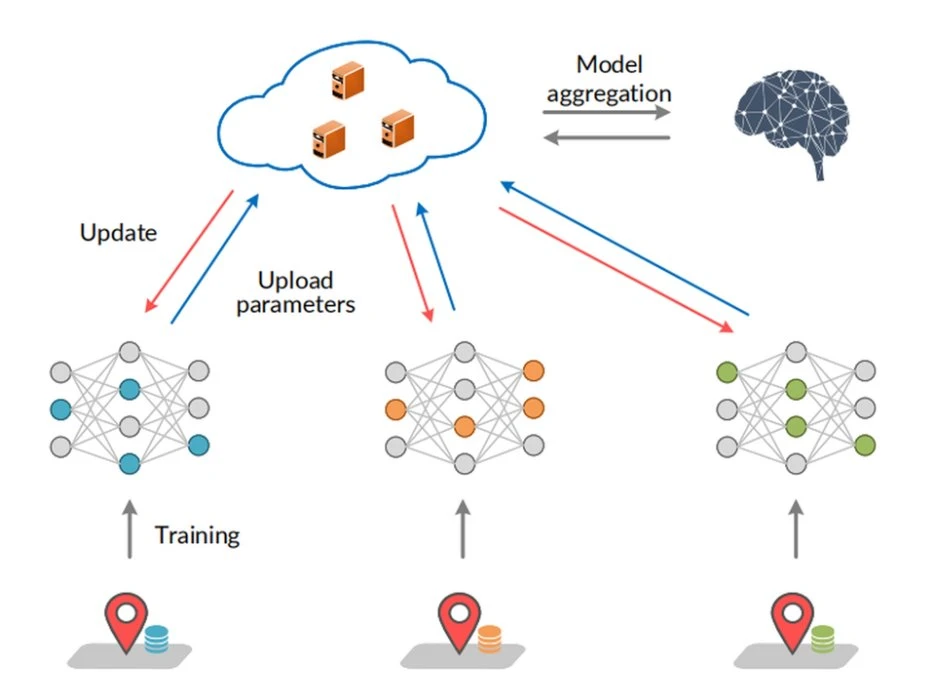
与此同时，Google AI 团队在 2016 年提出了联邦学习（Federated Learning）框架，将隐私计算概念直接融入到手机终端应用中。联邦学习允许数据在设备本地进行训练，再将模型参数集中整合，无需直接上传敏感数据。这一方法不仅提高了数据安全性，还显著增强了用户隐私保护能力。

该图展示了联邦学习的基本流程，说明了如何在不共享原始数据的情况下，通过本地模型训练和参数聚合，实现分布式机器学习

有趣的是，Google 联邦学习项目最初的内部代号为“蜜蜂计划”，寓意多个终端像蜜蜂一样分别贡献并汇聚成整体的智能模型。这个生动的比喻也展示了隐私计算技术如何从抽象理论走向实际生活中的广泛应用。

四、应用期（2019 年– 2024 年）：隐私计算走向实用

2019 年：联邦迁移学习与 FATE 系统的诞生

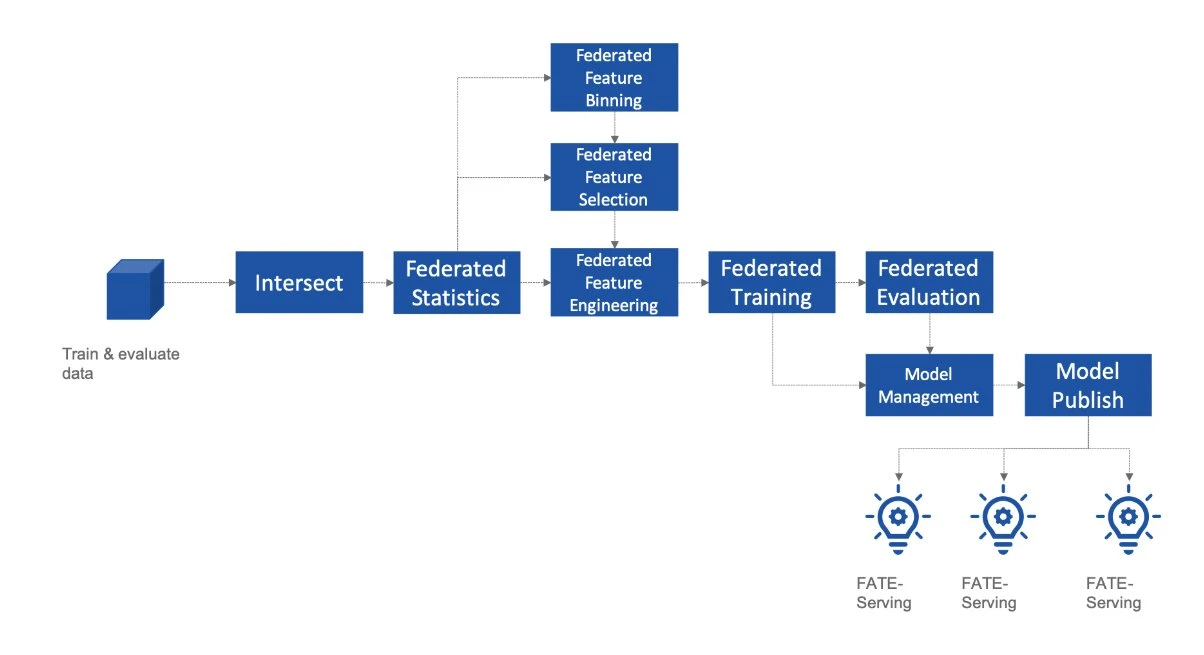
2019 年，香港科技大学的杨强教授及其团队正式推出联邦迁移学习（Federated Transfer Learning）理论与开源系统 FATE（Federated AI Technology Enabler），极大推动了联邦学习技术的产业化与工程化进展。杨强团队的研究创新性地将联邦学习与迁移学习结合，使不同领域、不同场景的数据在不共享原始数据的情况下实现模型迁移和知识共享，从而解决了数据孤岛问题。

该图展示了 FATE 系统的架构，说明了如何通过联邦学习实现跨机构的数据协作与模型训练

趣闻轶事是，在 FATE 系统正式开源发布大会上，由于业界对这项技术的高度关注，参与人数远超预期，以致于主办方不得不临时更换更大的场地。这一轶事也反映出业界对联邦学习落地应用的极大兴趣与热情。

FATE 系统的问世不仅推动了联邦学习技术快速落地，更为后续的数据合作提供了技术框架，被迅速应用到金融风控、医疗诊断、智能政务等实际场景中，为数据共享与隐私保护提供了实质性解决方案。

隐私计算成为数据基础设施

随着数据时代的到来，数据要素市场快速发展，数据安全与隐私保护逐渐成为各行业关注的核心问题。同时，各国数据合规性要求持续提升，促使隐私计算技术迅速与金融、医疗、政务等重要行业深度融合。

在金融领域，隐私计算技术如同态加密（FHE）、安全多方计算（MPC）和零知识证明（ZKP）等技术被广泛用于风险控制和反欺诈场景，确保数据使用安全合规。在医疗领域，差分隐私（DP）和联邦学习（FL）技术有效保护了患者隐私，促进了跨机构医疗研究和协作。

政务领域则积极采用可信执行环境（TEE）技术，构建安全高效的政务数据处理平台，保障敏感信息安全和公共信任。这些技术的协同使用极大提高了数据价值的释放速度，提升了数据共享效率和安全性。

技术协同与产业融合

当前阶段，密码学领域的多种核心技术，包括零知识证明（ZKP）、安全多方计算（MPC）、全同态加密（FHE）、可信执行环境（TEE）、差分隐私（DP）和联邦学习（FL）等逐步走向协同共生的发展路径。这种技术融合不仅丰富了隐私保护的手段，更提升了隐私计算整体的实用性与可靠性。

隐私计算已经不再停留在理论研究阶段，而是真正成为一种广泛应用的基础设施，支撑起数据要素的安全流通和价值共享，形成了以“隐私计算+产业”的新生态。未来，隐私计算技术将进一步融入各行业数字化转型过程中，成为推动产业创新、经济发展和社会进步的重要引擎。

这些丰富的理论探索与技术落地案例，标志着密码学与隐私计算从理论研究真正走向实践应用的新高度，也为高性能密码应用的发展奠定了稳固的基础。

五、密码学走向千家万户（2025 年至今）：ZEROBASE 阶段

2025 年：ZEROBASE 的崛起与普惠隐私计算

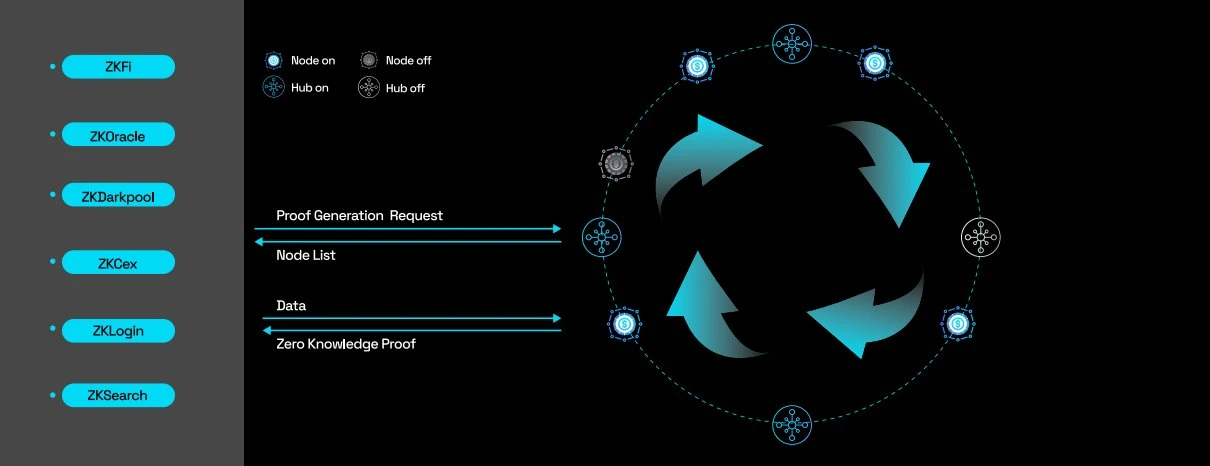
在 ZEROBASE 网络中，节点被划分为不同的子集，每个子集由一个 HUB 管理。每个 HUB 只记录其负责的 NODE 的状态信息，这意味着 NODE 只与其相应的 HUB 通信。在这种架构中，即使 NODE 数量增加，通过添加更多 HUB，系统也可以继续平稳运行

2025 年，隐私计算进入了一个全新阶段——ZEROBASE 阶段。ZEROBASE 项目以其独特的方式，将隐私计算带入了普通用户的日常生活中。ZEROBASE 的愿景是构建一个全球化的零知识（ZK）信任基础设施，支持金融、政务、医疗等多个领域的隐私计算应用落地。

ZEROBASE 采用了一种去中心化、易用的架构，以降低用户参与隐私计算的技术门槛。他重新设计了零知识证明（ZKP）系统的可信设置流程，首次以浏览器结合图像熵源的形式完成可信设置（Trusted Setup）。

ZEROBASE 的吉尼斯世界记录密码学挑战预热活动页面

2025 年初，ZEROBASE 发起了一项吉尼斯世界纪录挑战，在预热阶段成功吸引 564, 000 多名全球用户在 OKX Wallet 参与预热活动。

ZEROBASE：技术创新与社会共识

ZEROBASE 将复杂的技术通过用户友好的交互方式呈现，仅需简单的图像上传和浏览器操作，即可实现过去高度复杂的可信设置。这种设计理念不仅降低了参与门槛，更将 ZK 技术变成了一项社会化活动，极大提升了公众对隐私计算技术的认知和接受度。

技术层面上，ZEROBASE 开发了高度优化的 ZKP 电路，实现了每秒超过 1000 次的证明生成速度，这使得 ZEROBASE 在 ZK 证明市场中迅速占据领先地位。同时，ZEROBASE 还推出了多个创新应用，包括 zkLogin（无摩擦的Web3认证）、zkCEX（链上订单匹配与链下结算的混合交易所模式）和 zkStaking（验证套利风险、优化收益生成的抵押系统）。

ZEROBASE 吉尼斯世界纪录挑战的重要意义

ZEROBASE 发起的吉尼斯世界纪录挑战不仅仅是一场技术突破，更是一种社会叙事的转变。与传统的可信设置仪式不同，ZEROBASE 此次挑战将隐私计算从神秘的“黑箱”变成了开放、透明、可参与的社会事件。通过大众化的参与方式与公开透明的验证流程，ZEROBASE 有效解决了 ZK 技术长期以来的 信任 与 共识 难题。

我真的很喜欢斯蒂芬·霍金，在 ZEROBASE 游乐场你可以驾驶霍金，让他旋转和跳跃。哦，我是世界上最聪明的人！让我们乘坐时速 70 英里的飞行轮椅——由霍金本人驾驶！

此次吉尼斯世界纪录挑战不仅证明了隐私计算技术可以实现大规模公众参与，更表明了技术普惠与社会共识的重要性。这一点明确指出了隐私计算技术的未来不在于复杂的技术堆叠，而在于能否为普通用户提供无门槛的参与途径。

游乐场入口： https://zerobase.pro/playground/index.html

未来目标：构建全球化的隐私计算基础设施

随着隐私计算逐步走出实验室，它正在悄然重塑人类协作的底层秩序。未来，我们或许不再需要为每一次数据共享焦虑，因为保护隐私将成为系统默认的“基础权利”；一个农民可以用隐私算法预测气候变化，一个社区可以在 DAO 中无中介地管理公共事务，一位身处偏远地区的患者也能用可信 AI 安全共享病例、获得全球最优解。

更远的未来，或许我们还将见证隐私计算在量子时代为文明提供最后一道防线，成为数字社会可信运行的“安全恒星”。

回望今天，这场变革或许才刚刚开始。 但正如互联网从协议走向世界，隐私计算也终将走向每一个普通人。

真正值得铭记的，不是某一次技术的飞跃，而是我们共同选择以何种方式，走向一个更自由、更安全、更可信的数字文明。

Refe rence

[ 1 ] Shamir A. How to share a secret. Commun ACM. 1979 Nov;22( 11): 612 – 3.

[ 2 ] Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theory. 1976 Nov;22( 6): 644 – 54.

[ 3 ] Calderbank. The rsa cryptosystem: history, algorithm, primes. Chicago: math uchicago edu [Internet].

[ 4 ] Yao AC. Protocols for secure computations. In: 23 rd Annual Symposium on Foundations of Computer Science (sfcs 1982). 1982. p. 160 – 4.

[ 5 ] Shannon CE. Communication theory of secrecy systems. The Bell System Technical Journal. 1949 Oct;28( 4): 656 – 715.

[ 6 ] Blakley. Safeguarding cryptographic keys. In: Managing Requirements Knowledge, International Workshop on. 1979. p. 313.

[ 7 ] Rabin MO. How To Exchange Secrets with Oblivious Transfer. Cryptology ePrint Archive [Internet]. 2005 [cited 2022 May 28 ];

[ 8 ] Rivest RL, Adleman L, Dertouzos ML. On data banks and privacy homomorphisms. Foundations of secure [Internet]. 1978;

[ 9 ] Goldwasser S, Micali S, Rackoff C. The knowledge complexity of interactive proof-systems [Internet]. Proceedings of the seventeenth annual ACM symposium on Theory of computing - STOC ’ 85. 1985.

[ 10 ] Yao ACC. How to generate and exchange secrets. In: 27 th Annual Symposium on Foundations of Computer Science (sfcs 1986). 1986. p. 162 – 7.

[ 11 ] Goldreich O, Micali S, Wigderson A. How to Play ANY Mental Game. In: Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing. New York, NY, USA: ACM; 1987. p. 218 – 29. (STOC ’ 87).

[ 12 ]  Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theory. 1976 Nov;22( 6): 644 – 54.

[ 13 ] Paillier P. Public-Key Cryptosystem Based on Discrete Logarithm Residues. EUROCRYPT 1999 [Internet].

[ 14 ] Dwork C. Differential Privacy. In: Automata, Languages and Programming. Springer Berlin Heidelberg; 2006. p. 1 – 12.

[ 15 ] Hardware Working Group. ADVANCED TRUSTED ENVIRONMENT: OMTP TR 1 [Internet]. OMTP Limited; 2009.

[ 16 ] Gentry C. A fully homomorphic encryption scheme [Internet]. 2009. Available

[ 17 ] Wang S, Jiang X, Wu Y, Cui L, Cheng S, Ohno-Machado L. EXpectation Propagation LOgistic REgRession (EXPLORER): distributed privacy-preserving online model learning. J Biomed Inform. 2013 Jun;46( 3): 480 – 96.

[ 18 ] Gao D, Liu Y, Huang A, Ju C, Yu H, Yang Q. Privacy-preserving Heterogeneous Federated Transfer Learning. In: 2019 IEEE International Conference on Big Data (Big Data). 2019. p. 2552 – 9.

[ 19 ] Kone ny J, Brendan McMahan H, Yu FX, Richtárik P, Suresh AT, Bacon D. Federated Learning: Strategies for Improving Communication Efficiency [Internet]. arXiv [cs.LG]. 2016.

[ 20 ] Intel. Intel Architecture Instruction Set Extensions Programming Reference [Internet]. Intel; 2015.