Vitalik Buterin：隐身地址的不完全指南

原文作者： Vitalik Buterin

原文编译： DeFi 之道

特别感谢 Ben DiFrancesco、Matt Solomon、Toni Wahrstätter 和 Antonio Sanso 的反馈和审阅。

以太坊 生态系统中剩下的最大挑战之一是隐私。 默认情况下，进入公共 区块链 的任何内容都是公开的。 越来越多地，这不仅意味着金钱和 金融 交易，还意味着 ENS 域名、POAP、 NFT 、灵魂绑定代币等等。 在实践中，使用整套以太坊应用程序涉及将你生活的重要部分公开给任何人查看和分析。

如何改善这种状况已经成为一个重要的问题，这一点已得到广泛认可。 然而，到目前为止，关于改善隐私的讨论主要围绕一个特定的用例： ETH 和主流 ERC 20 代币的隐私保护转移（通常是自我转移）。 这篇文章将描述一种不同类别的工具的机制和用例，这些工具可以在许多其他情况下改善以太坊的隐私状态：隐身地址。

什么是隐身地址系统？

假设 Alice 想给 Bob 一个资产。 这可能是一定数量的加密 货币 （例如 1 ETH、 500 RAI），也可能是一个 NFT。 当 Bob 收到资产时，他不想让全世界都知道是他得到的。 想要隐藏一笔转账发生的事实是不可能的，特别是如果它是一个链上只有一个副本的 NFT，但隐藏谁是接收者可能更可行。 Alice 和 Bob 也很懒惰：他们想要一个支付流程与今天完全相同的系统。 Bob 向 Alice（或在 ENS 上注册）发送某种“地址”编码，编码某人如何向他付款，仅此信息就足以让 Alice（或其他任何人）向他发送资产。

请注意，这与 Tornado Cash 等工具提供的隐私不同。Tornado Cash 可以隐藏 ETH 或主要的 ERC 20 代币等主流可替代资产的转账（尽管它最容易用于私下发送给自己），但它在为不知名的 ERC 20 转账添加隐私方面非常薄弱，并且它无法为 NFT 转账添加隐私。

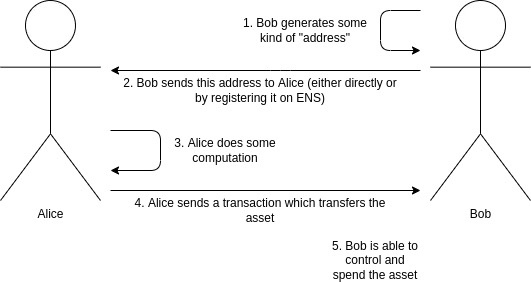
使用 加密货币 进行支付的普通工作流程。 我们想增加隐私（没有人能知道是 Bob 收到了资产），但保持工作流程不变。

隐身地址提供了这样的方案。 隐身地址是可以由 Alice 或 Bob 生成的地址，但只能由 Bob 控制。 Bob 生成并保密一个支出密钥，并使用该密钥生成一个隐形元地址。 他将这个元地址传递给 Alice（或在 ENS 上注册）。 Alice 可以对该元地址执行计算以生成属于 Bob 的隐形地址。 然后她可以将她想发送的任何资产发送到这个地址，Bob 将完全控制这些资产。 随着转移，她在链上发布了一些额外的加密数据（一个临时公钥），帮助 Bob 发现这个地址属于他。

另一种方式是：隐身地址提供与 Bob 相同的隐私属性，为每笔交易生成一个新地址，但不需要 Bob 的任何交互。

隐身地址方案的完整工作流程如下所示：

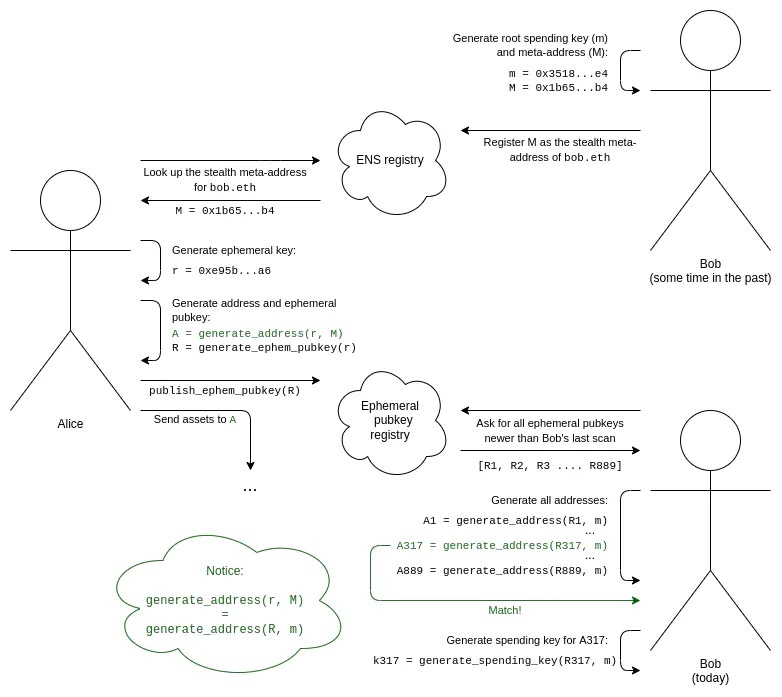
1. Bob 生成他的根支出密钥 (m) 和隐形元地址 (M)。

2. Bob 添加一条 ENS 记录以将 M 注册为 bob.eth 的隐形元地址。

3. 我们假设 Alice 知道 Bob 是 bob.eth。 Alice 在 ENS 上查找他的隐身元地址 M。

4. Alice 生成一个只有她知道的临时密钥，并且她只使用一次（生成这个特定的隐形地址）。

5. Alice 使用一种算法，将她的临时密钥和 Bob 的元地址结合起来生成一个隐身地址。 她现在可以将资产发送到这个地址。

6. Alice 还生成了她的临时公钥，并将其发布到临时公钥注册表（这可以在与将资产发送到该隐身地址的第一笔交易相同的交易中完成）。

7. 为了让 Bob 发现属于他的隐身地址，Bob 需要扫描临时公钥注册表以查找自上次扫描以来任何人出于任何原因发布的整个临时公钥列表。

8. 对于每个临时公钥，Bob 尝试将其与他的根支出密钥结合起来生成一个隐形地址，并检查该地址中是否有任何资产。 如果有，Bob 计算该地址的支出密钥并记住它。

这一切都依赖于密码欺骗的两种用途。 首先，我们需要一对算法来生成共享秘密：一个算法使用 Alice 的秘密事物（她的临时密钥）和 Bob 的公开事物（他的元地址），另一个算法使用 Bob 的秘密事物（他的根花费密钥） ) 和 Alice 的公开事物（她的临时公钥）。 这可以通过多种方式完成； Diffie-Hellman 密钥交换是建立现代密码学领域的成果之一，它也正是实现了这一点。

但是仅共享秘密是不够的：如果我们只是从共享秘密生成一个私钥，那么 Alice 和 Bob 都可以从这个地址消费。 我们可以就此打住，让 Bob 将资金转移到新地址，但这样做效率低下并且不必要地降低了 安全 性。 所以我们还添加了一个密钥盲化机制：一对算法，Bob 可以将共享秘密与他的根支出密钥结合起来，Alice 可以将共享秘密与 Bob 的元地址结合起来，这样 Alice 就可以生成隐身地址 ，并且 Bob 可以为该隐身地址生成支出密钥，所有这些都无需在隐身地址和 Bob 的元地址之间（或一个隐身地址与另一个隐身地址之间）创建公共链接。

使用椭圆曲线密码术的隐身地址

使用椭圆曲线密码术的隐身地址最初是由 Peter Todd 于 2014 年在 比特币 的背景下引入的。该 技术 的工作原理如下（这假定了基本椭圆曲线密码技术的先验知识；请参见此处、此处和此处以获取一些教程）：

• Bob 生成一个密钥 m，并计算 M = G * m，其中 G 是椭圆曲线的共同商定生成点。 隐形元地址是 M 的编码。

• Alice 生成一个临时密钥 r，并发布临时公钥 R = G * r。

• Alice 可以计算出一个共享秘密 S = M * r，而 Bob 可以计算出相同的共享秘密 S = m * R。

• 一般来说，在比特币和以太坊（包括正确设计的 ERC-4337 账户）中，地址是包含用于验证来自该地址的交易的公钥的哈希。 因此，如果您计算公钥，就可以计算地址。 为了计算公钥，Alice 或 Bob 可以计算 P = M + G * hash(S)

• 为了计算该地址的私钥，Bob（和 Bob 一个人）可以计算 p = m + hash(S)这满足了我们上面的所有要求，而且非常简单！

今天甚至有一个 EIP 试图为以太坊定义一个隐身地址标准，它既支持这种方法，又为用户提供了开发其他方法的空间（例如，支持 Bob 拥有单独的支出和查看密钥，或者使用不同的密码学来实现抗量子安全）。 现在你可能会想：隐身地址并不难，理论已经扎实，采用只是一个实现细节。 然而，问题在于，真正有效的实施需要通过一些相当大的实施细节。

隐身地址和支付交易费用

假设有人给你发了一个 NFT。 考虑到您的隐私，他们会将其发送到您控制的一个隐身地址。 扫描链上的 ephem 公钥后，您的 钱包 会自动发现该地址。 您现在可以自由证明这个 NFT 的所有权或将其转让给其他人。 但是有一个问题！ 该帐户中的 ETH 为 0 ，因此无法支付交易费用。 即使是 ERC-4337 代币付款人也不会工作，因为它们只适用于可替代的 ERC 20 代币。 而且你不能从你的主钱包向它发送 ETH，因为那样你就创建了一个公开可见的链接。

插入 2017 年（或更早）加密骗局人物的模因是作家可以用来表示博学和受人尊敬的一项重要技术，因为这表明他们已经入圈很长时间并且品味高雅，并且不容易被像 SBF 这样的人所骗。

有一种“简单”的方法可以解决这个问题：只需使用 ZK-SNARKs 转移资金来支付费用！ 但是这样会消耗大量的 gas，单次转账就多了几十万 gas。

另一种聪明的方法涉及信任专门的交易聚合器（ MEV 术语中的“搜索者”）。 这些聚合器将允许用户支付一次以购买一组可用于支付链上交易的“票”。 当用户需要在一个不包含任何其他内容的隐身地址中花费 NFT 时，他们会向聚合器提供其中一张票，使用 Chaumian 盲化方案进行编码。 这是在 1980 年代和 1990 年代提出的中心化隐私保护电子现金方案中使用的原始协议。 搜索者接受“票”，并重复将交易免费包含在他们的捆绑包中，直到交易在一个区块中被成功接受。 由于涉及的资金量少，而且只能用于支付交易手续费，因此信任和监管问题远低于“完全”实施这种中心化隐私保护电子现金。

隐身地址和分离支出和查看密钥

假设 Bob 不是只有一个可以做所有事情的主“根支出密钥”，而是想要一个单独的根支出密钥和查看密钥。 查看密钥可以看到 Bob 的所有隐形地址，但不能从中花费。

在椭圆曲线世界中，这可以使用一个非常简单的密码技巧来解决：

• Bob 的元地址 M 现在的形式为 (K, V)，编码为 G * k 和 G * v，其中 k 是支出密钥，v 是查看密钥。

• 共享秘密现在是 S = V * r = v * R，其中 r 仍然是 Alice 的临时密钥，R 仍然是 Alice 发布的临时公钥。

• 隐身地址的公钥是 P = K + G * hash(S)，私钥是 p = k + hash(S)。

请注意，第一个聪明的加密步骤（生成共享秘密）使用查看密钥，第二个聪明的加密步骤（Alice 和 Bob 的并行算法生成隐身地址及其私钥）使用根支出密钥。

这有很多用例。 例如，如果 Bob 想要接收 POAP，那么 Bob 可以给他的 POAP 钱包（或者甚至是一个不太安全的 Web 界面）他的查看密钥来扫描链并查看他的所有 POAP，而不需要给这个界面花费那些 POAP 的权力。

隐身地址和更容易扫描

为了更容易地扫描整个临时公钥集，一种技术是向每个临时公钥添加一个视图标签。 在上述机制中执行此操作的一种方法是使视图标签成为共享秘密的一个字节（例如，S 模 256 的 x 坐标，或 hash(S) 的第一个字节）。

这样，Bob 只需要为每个临时公钥执行一次椭圆曲线乘法来计算共享秘密，而 Bob 需要进行更复杂的计算以生成和检查完整地址的时间只有 1/256 。

隐身地址和抗量子安全

上面的方案依赖于椭圆曲线，它很好，但不幸的是容易受到量子计算机的攻击。 如果量子计算机成为一个问题，我们将需要切换到抗量子算法。 有两个自然的候选者：椭圆曲线同源和格（lattices）。

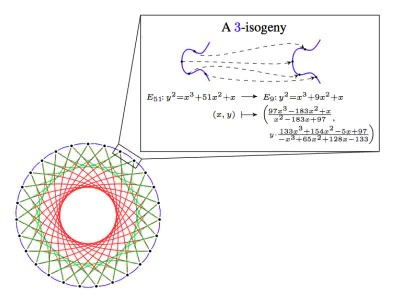
椭圆曲线同源是一种非常不同的基于椭圆曲线的数学构造，它具有线性特性，可以让我们使用与上面所做的类似的密码技巧，但巧妙地避免了构造可能容易受到量子计算机离散对数攻击的循环群。

基于同源性的密码学的主要弱点是其高度复杂的底层数学，以及在这种复杂性下隐藏可能的攻击的风险。 去年，一些基于同种基因的协议被攻破，但其他协议仍然安全。 同源性的主要优势是相对较小的密钥大小，以及直接移植多种基于椭圆曲线的方法的能力。

CSIDH 中的 3-同源性，来源在这里。

格（Lattices）是一种非常不同的密码结构，它依赖于比椭圆曲线同构简单得多的数学，并且能够完成一些非常强大的事情（例如全同态加密（FHE））。 隐形地址方案可以建立在格上，尽管设计最好的方案是一个悬而未决的问题。 然而，基于格的结构往往具有更大的密钥大小。

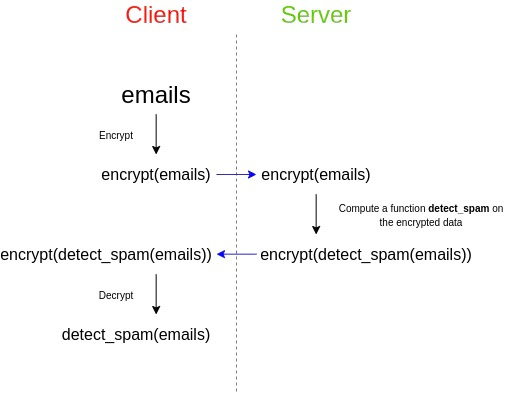
全同态加密，这是格的一种应用。 FHE 还可以用于以不同的方式帮助隐形地址协议：帮助 Bob 外包检查整个链中是否包含资产的隐形地址的计算，而无需透露他的视图密钥。

第三种方法是从通用黑盒原语构建隐身地址方案：许多人出于其他原因需要的基本成分。 该方案的共享秘密生成部分直接映射到密钥交换，这是公钥加密系统中的一个重要组成部分。 更难的部分是让 Alice 只生成隐形地址（而不是支出密钥）并让 Bob 生成支出密钥的并行算法。

不幸的是，您无法使用比构建公钥加密系统所需的成分更简单的成分来构建隐形地址。 有一个简单的证明：你可以用一个隐蔽的地址方案构建一个公钥加密系统。 如果 Alice 想给 Bob 加密一条消息，她可以发送 N 笔交易，每笔交易要么发往 Bob 的一个隐身地址，要么发往一个属于她自己的隐身地址，Bob 可以看到他收到了哪些交易来读取消息。 这很重要，因为有数学证明你不能只用哈希来做公钥加密，而你可以只用哈希来做零知识证明——因此，隐形地址不能只用哈希来完成。

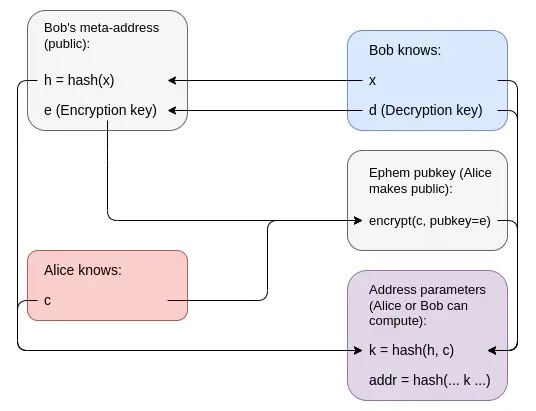
这是一种确实使用相对简单成分的方法：零知识证明，可以由哈希和（密钥隐藏）公钥加密组成。 Bob 的元地址是一个公开的加密密钥加上一个哈希 h = hash(x)，他的支出密钥是对应的解密密钥加上 x。 为了创建一个隐身地址，Alice 生成一个值 c，并将 Bob 可读的 c 加密作为她的临时公钥发布。 地址本身是一个 ERC-4337 帐户，其代码通过要求交易提供零知识证明来验证交易，证明值 x 和 c 的所有权，使得 k = hash(hash(x), c)（其中 k 是 账户代码）。 知道 x 和 c，Bob 可以自己重建地址及其代码。

c 的加密不会告诉 Bob 任何其他人任何信息，而且 k 是一个哈希，因此它几乎不会透露任何关于 c 的信息。 钱包代码本身只包含 k，c 是私有的，意味着 k 无法追溯到 h。

然而，这需要一个 STARK，而 STARK 很大。 最终，我认为后量子以太坊世界很可能会涉及许多应用程序使用许多 Stark，因此我提倡像此处描述的聚合协议将所有这些 STARK 组合成一个递归 STARK 以节省空间。

隐身地址和社交恢复以及多 L2 钱包

很长一段时间以来，我一直是社交恢复钱包的粉丝：具有多重签名机制的钱包，其密钥在机构、您的其他设备和您的朋友之间共享，其中一些绝大多数密钥可以恢复对您帐户的访问，除非您丢失主秘钥。

然而，社交恢复钱包不能很好地与隐身地址混合：如果你必须恢复你的账户（意思是，改变控制它的私钥），你还必须执行一些步骤来改变你的 N 个隐身钱包的账户验证逻辑 ，这将需要 N 笔交易，以高昂的费用、便利性和隐私成本为代价。

社交恢复和多个第 2 层协议的世界的相互作用也存在类似的担忧：如果你在 Optimism 、 Arbitrum 、Starknet、Scroll、 Polygon 有账户，并且可能其中一些 rollups 上出于扩展原因有十几个并行实例，并且您在每个实例上都有一个帐户，那么更改密钥可能是一个非常复杂的操作。

更改多个链中多个帐户的密钥是一项巨大的工作。

一种方法是硬着头皮接受恢复是罕见的，而且代价高昂和痛苦是可以接受的。 也许您可以使用一些自动化软件在两周的时间跨度内以随机间隔将资产转移到新的隐蔽地址，以降低基于时间的链接的有效性。 但这远非完美。 另一种方法是在监护人之间秘密共享根密钥，而不是使用 智能合约 恢复。 但是，这会消除停用监护人帮助恢复您帐户的权力的能力，因此存在长期风险。

一种更复杂的方法涉及零知识证明。 考虑上面基于 ZKP 的方案，但修改逻辑如下。 账户不是直接持有 k = hash(hash(x), c)，而是持有（隐藏）链上 k 位置的承诺。 从该账户支出然后需要提供一个零知识证明（i）你知道链上与该承诺匹配的位置，以及（ii）该位置的对象包含一些值 k（你没有透露） ，并且你有一些值 x 和 c 满足 k = hash(hash(x), c)。

这允许许多帐户，甚至跨越许多第 2 层协议，在某处（在基础链上或某些第 2 层上）由单个 k 值控制，其中更改一个值足以更改所有帐户的所有权 ，所有这些都不会泄露您的帐户之间的联系。

结论

基本的隐身地址今天可以相当快地实施，并且可以显着提高以太坊上的实际用户隐私。 他们确实需要在钱包方面做一些工作来支持他们。 也就是说，我认为出于其他与隐私相关的原因，钱包应该开始转向更原生的多地址模型（例如，为您与之交互的每个应用程序创建一个新地址可能是一种选择）。

然而，隐身地址确实会带来一些长期的可用性问题，例如社交恢复的困难。 现在可以简单地接受这些担忧，例如。 通过接受社交恢复将涉及隐私的丧失或延迟两周以缓慢地将恢复交易发布到各种资产（这可以由第三方服务处理）。 从长远来看，这些问题是可以解决的，但从长远来看，隐身地址生态系统看起来确实严重依赖于零知识证明。