五分钟读懂 Pendle AMM：交易随时间衰减资产的魔法工具

Pendle AMM 不仅支持收益代币，期权、债券等其他具有时间衰减特性的资产同样适用。

撰文：Pendle
编译：Perry Wang

我们认为，收益型代币与传统金融中的利率衍生品类似，对于在去中心化金融（DeFi）世界中建立有效的货币市场至关重要。Pendle 通过从带有收益的代币中剥离出收益，创建了代表对未来收益具有所有权的特有代币。

然后，这些代币可以在 Pendle 的自动做市商 AMM 上进行交易，使交易者能够针对收益率的波动进行投机、对冲或套利。

但是，首先为什么我们需要为这些收益代币使用 AMM 呢？

与时间有关的损失

收益代币的价值与时间息息有关。 随着时间的流逝，收益代币的持币者获得的收益会趋于减少，并且一旦不再收集任何收益，该代币最终将在到期时变得一文不值。 在典型的 AMM 上，交易那些受时间衰减影响的代币的效率极低，因为它肯定将为流动性提供者（LP ）带来无常损失（Impermanent Loss, IL）。

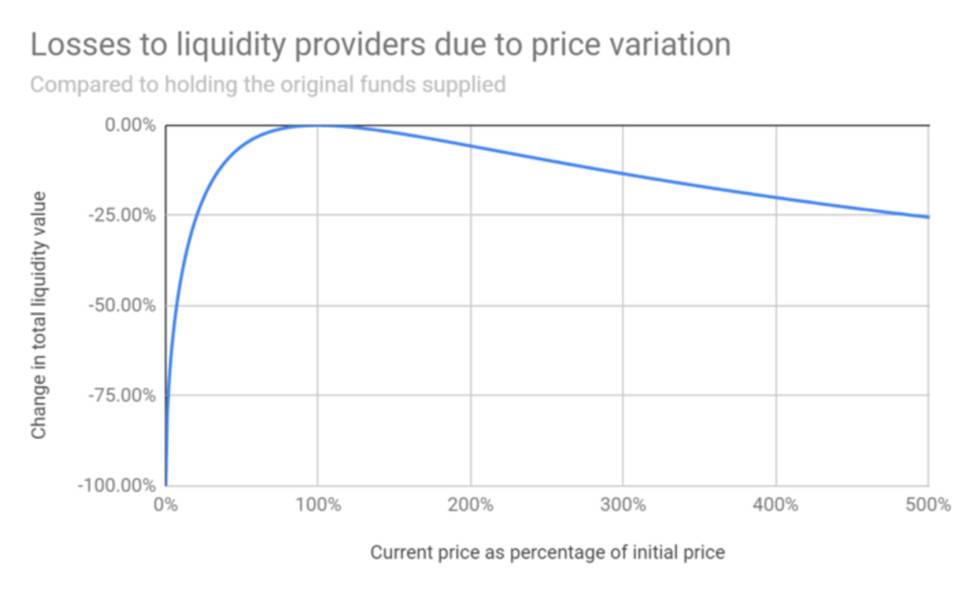
无常损失是在 AMM 中提供流动性所获价值与将其保存在钱包中之间的价值差。 当典型的恒定乘积 AMM 中的代币价格在任何方向上发生偏离时，就会出现这种情况。 偏差越大，无常损失就越大（如果在那一刻撤回流动性，无常损失将变成永久性损失）。

对于收益代币或任何随时间衰减的资产，恒定乘积 AMM 中的无常损失都是不可避免的。 这是因为把价格发现留给了市场参与者和套利者。 通过套利者进行交易，逐渐将典型的 x * y = k 曲线的平衡点移动至认知中的市场公允价值。 价值的变化是导致 LP 出现无常损失的原因。 由于收益代币的市场价值在到期时为 0，届时 LP 将遭受巨大损失，因为资金池的一侧已全部枯竭。

Pendle AMM 的设计

为了考虑进去时间衰减的因素，我们设计了一种 AMM，可满足所有具有时间衰减特性的资产。 最初创建流动性池后，AMM 曲线类似于 Uniswap 的恒定乘积曲线。 不过当发生后续交换时，AMM 曲线将在平衡点处移动，并自行调整以解决资产的时间衰减问题。

Pendle AMM 曲线随时间变化而变化

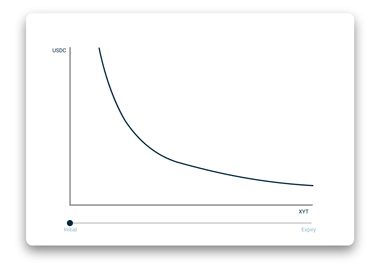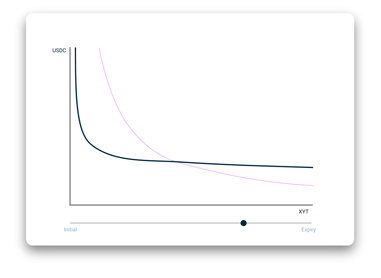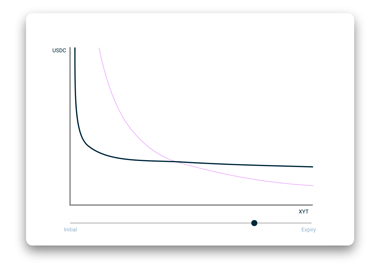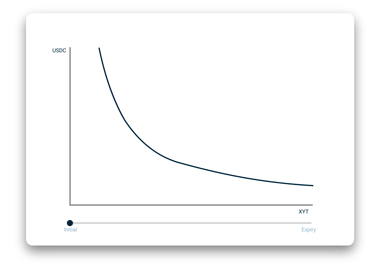
曲线移动会人为地将时间衰减代币的价格降低。曲线移动的行为由随时间衰减的定价模型来控制，而这一模型受债券或期权定价模型启发而来，而且，在合同期限内价值降低的速度趋于加快。 要了解曲线移位的更多详细信息，可以在我们的文档中找到。

Pendle 的 AMM 有效地打破了流动性池的价值与其基本代币价值之间的硬编码联系。 随时间变化的价值保留在流动性池中，否则该值会被恒定乘积曲线 AMM 上的套利者抢走。 假设我们的 AMM 的平衡点没有变化，那么 LP 将不会遭受任何与时间有关的损失。

与时间有关的无常损失 (Pendle vs Uniswap)

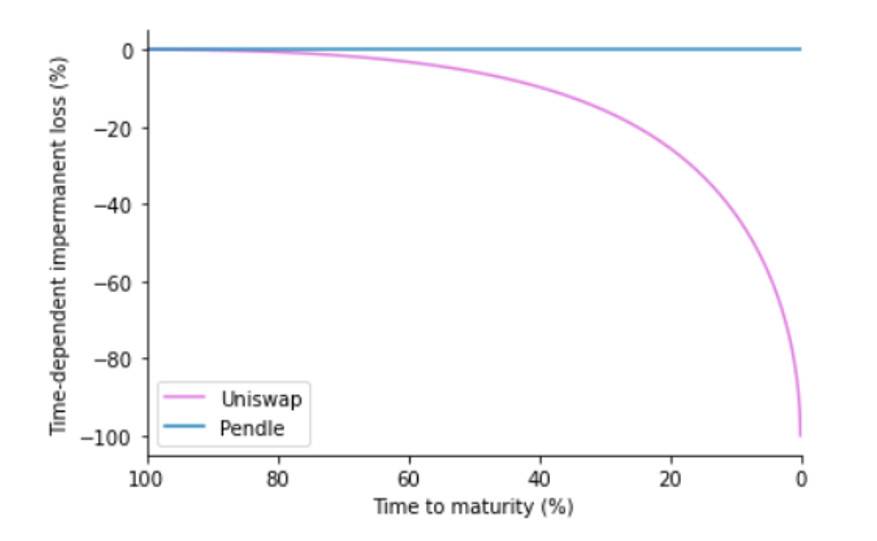
尽管我们一直将更多关注放在收益代币上，但 Pendle 的 AMM 可以扩展为支持具有时间衰减特性的任何类型资产。

使用 Pendle，可以交易期权、债券或任何包含有效期的合约。随着基于 DeFi 构建了越来越多的结构化产品，我们对未来发展充满信心。

来源链接： medium.com