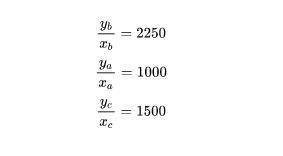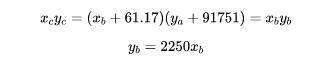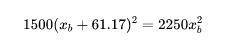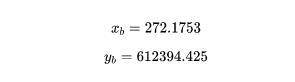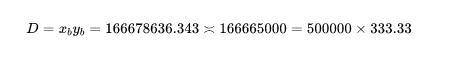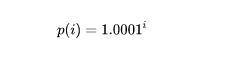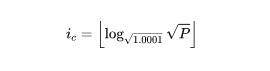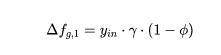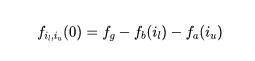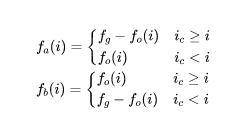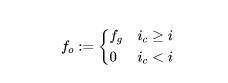Uni V3 的数学原理

作者：比原链研究院

前言——Uniswap V3 （如下简称 Uni V3）放出了很多 feature，然而其最为本质的迭代依然是对 AMM 数学曲线的再思考。在过去的两年中，我们也躬身入局 AMM 领域，认为 AMM 最基本的曲线形态已经定型，后续的创新应该会在 AMM 基本曲线形态的基础上实现“策略化”，于是我们创造了 MOV 超导 V2。而如今我们看到了 V3，突然有一种“久别重逢”的感觉，在寻找这种感觉之余，我们也希望为大家呈现 AMM 最为深刻的思考路程。因为 AMM 的时代将会比想象得更为恢弘壮阔。

让我们直切正题，Uniswap V3 最耀眼的创新——在 AMM 上实现集中流动性。

V3 给出了一个虚拟储备金（virtual reserves）的概念，举例讲解：

在传统 V2 中，Alice 一次性将 500,000 DAI 和 333.33 ETH 注入储备池，总价值 $1m，提供全区间 (0,\infty) 的流动性，但实际上 ETH 的价格波动范围在很长一段时间内是有局部范围的，这种为全区间无私提供流动性的行为大大浪费了资本利用效率。

（注：在一个逐步走向成熟化的金融市场中，无套利原理和提升资本利用效率永远是两大核心诉求，也是后续 DeFi 产品向先驱 DeFi 发起挑战的出发点。）

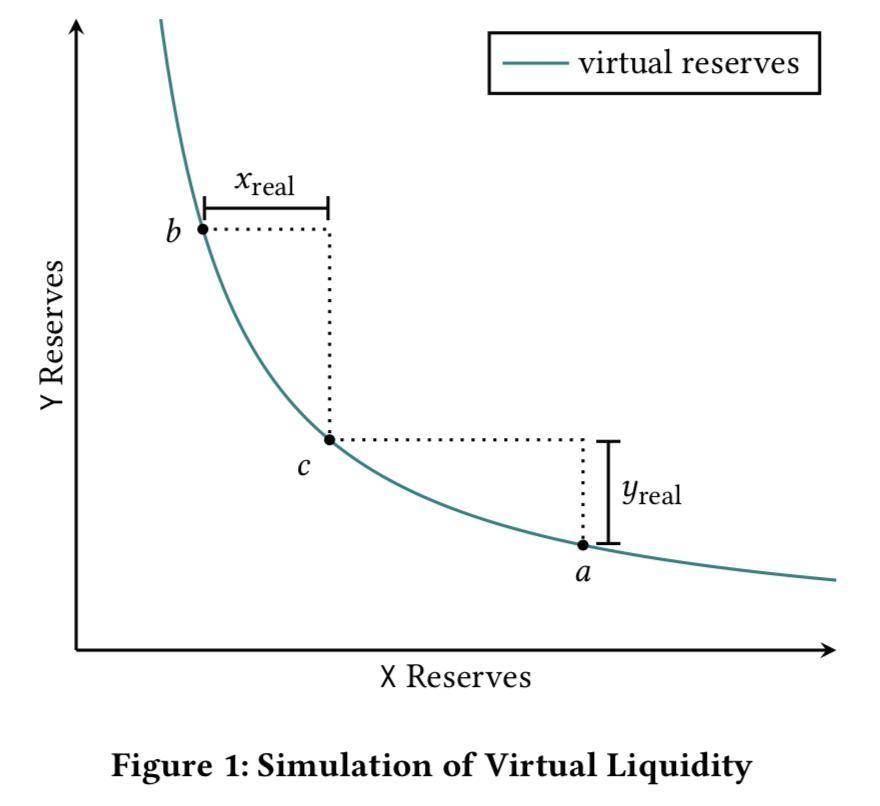
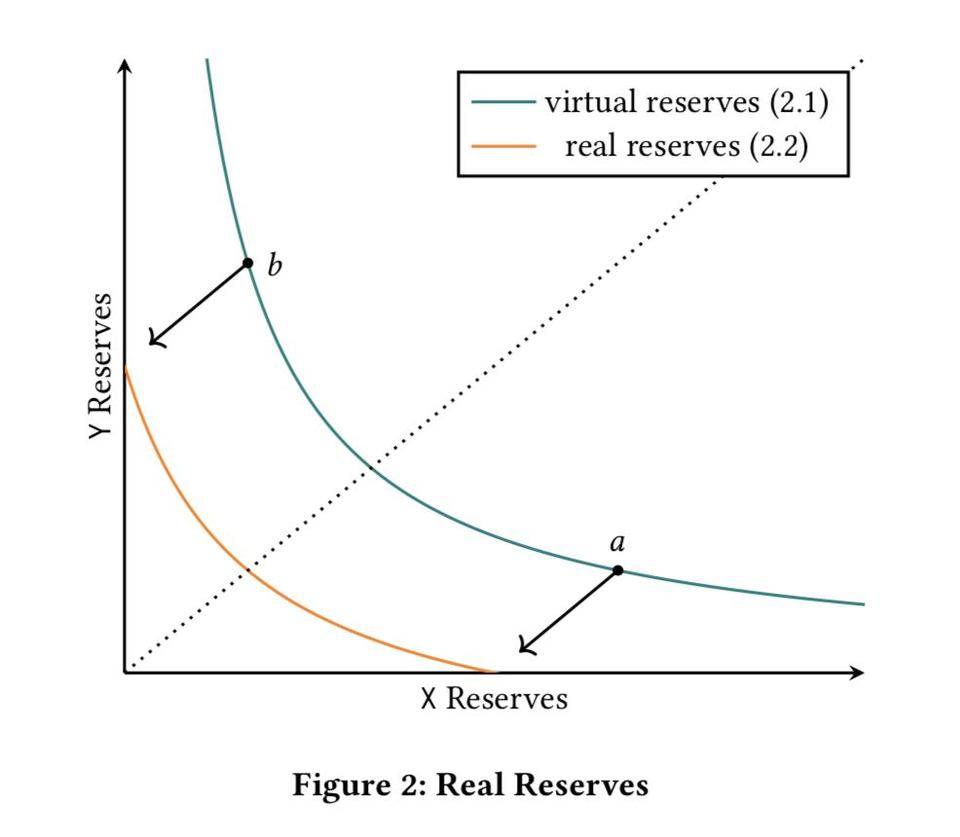
所谓的集中流动性便是让 LP 自主选择波动范围，只为该范围提供局部流动性，例如 Bob 认为未来一段时间内 ETH 的价格区间在 (1000,2250)，并且如果未来真的是在这个区间波动，Bob 希望自己获得的收益能够跟百万富豪 Alice 一样多，于是 Bob 一开始只需要投入 91,751 DAI 和 61.17 ETH，总价值 $183,500，远远小于 Alice 实际投入的资金。我们对照下图来解释其中的道理。

其中，X 是 ETH，Y 是 DAI，点 a 对应价格 1000，点 b 对应价格 2250，点 c 是当前市场价格 1500，x_{real}是 Bob 投入的 61.17 ETH，y_{real}是 91751 DAI。

在数学实现上——

假设图中曲线表达式为 xy=D，其中 D 便是我们要确定的值，即这条“虚拟的”曲线。

存在如下客观事实：

进一步，由于

则

解方程得

最后我们发现

即 Bob 所获得的虚拟曲线（D 值）几乎跟 Alice 一样。

上述计算过程是一种反证法，实际上用户 Bob 会向系统算法提出自己的需求输入，包括预测价格区间范围、当前价格点、最终想要获得的一个 virtual reserves 规模（即虚拟曲线 D 值）。有了虚拟曲线表达式的确定，可以轻松算出 a、b、c 三个确定的点坐标，进而便算出 x_{real}=61.17 以及 y_{real}=91751。

同时，也可以看到，一旦未来价格越出了区间，Bob 其中一种资产将彻底消失。

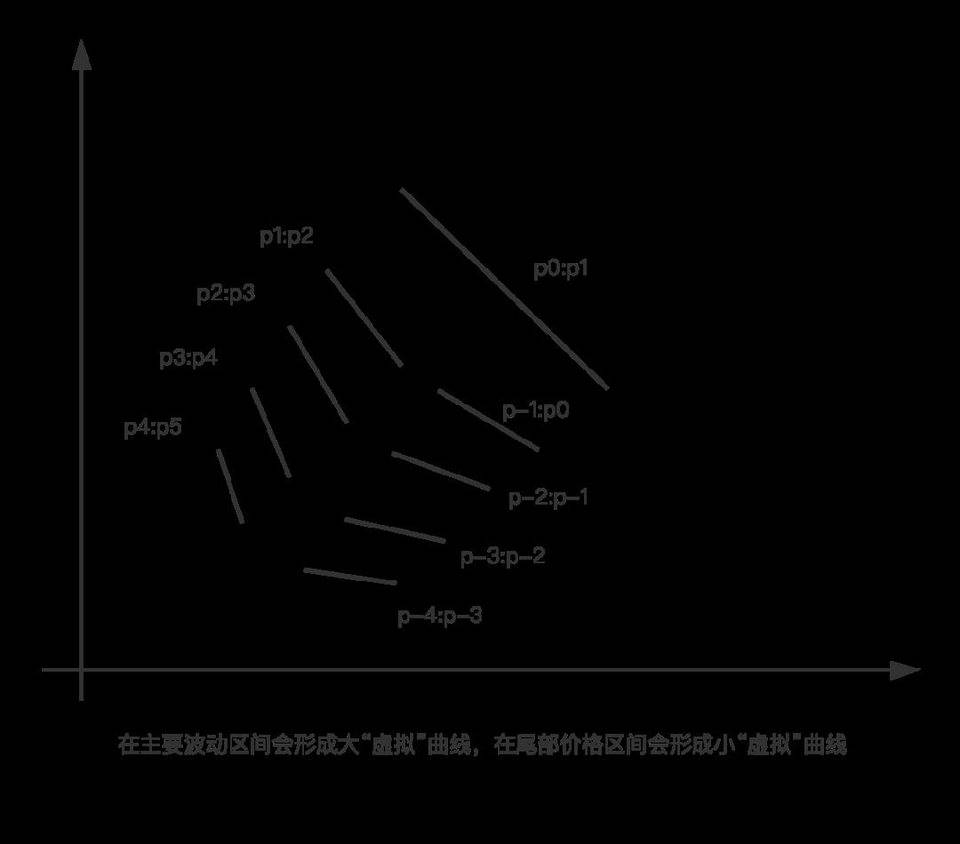
虚拟储备金（virtual reserve）是 Uni V3 实现集中流动性的基础原理，也是 Uni V3 将多样化的仓位区间统一成一条（大的全区间的虚拟）曲线的巧妙之处。然而看似简单的原理背后缺需要复杂的工程实现和算法模型的支撑，尤其是解决手续费（fee）的统计计算和 LP 的加入 / 退出计算。

对于 AMM 来说，最复杂的莫过于 LP 的存取行为和收益统计，在以 V2 为代表的经典 AMM 模型中，会通过一种“份额模式”从始至终为 LP 确定下各自可提取的数量比例（也包括手续费）。但在 V3 中，将会对 LP 可提取比例以及所获 fee 比例进行一种“非常统计风格”的计算方法。

在具体实现上，Uni V3 将价格全区间以 ticks 的模式均匀分段，变成离散的空间：

如何根据当前价格，判断所处 ticks——

全局状态中有 feeGrowthGlobal0(f_{g},0) 和 feeGrowthGlobal1 (f_{g},1)—f_{g}，用来从全局角度统计总的手续费收益。例如，当在一个 tick 内发生了一笔交易，系统会计算出该笔交易产生的手续费：

其中 y_{in}为该笔交易的输入数量，其余部分是手续费的比例。系统会不断累计出每个 tick 内产生的所有手续费总和。

再引入一个“稍微低一个级别的”全局状态变量 feeGrowthOutside\{0,1\}—f_{o}，用于计算在给定区间（range，由很多连续的 ticks 组成的空间）内的手续费总和。我们想查询某个价格 range （即在下界 tick i_{l}和上界 tick i_{u}之间）产生了多少累计手续费，总公式为：

其中，

f_{a}变量是对所有高于 i tick 的区间的 fee 统计，f_{b}是对所有低于 i tick 的区间的 fee 统计，因此在上述总公式中，我们从全局总累计手续费 f_{g}中减去所有低于下界 i_{l}的累计手续费，再减去所有高于上界 i_{u}的累计手续费，便是 (i_{l},i_{u}) 之间的累计手续费。

f_{o} 可以理解为一个计算单元，用于累积截止到 i tick 的手续费，在它的初始化过程中，我们约定如下：

再来看 f_{a}的计算，分成了两段，可以理解为——

• 如果当前 tick 等于 i 或者高于 i，此时从全局总手续费 f_{g} 中减去“累积到 i tick”的手续费 f_{o}(i)，剩下的便是对所有高于 i tick 的区间的 fee 统计；

• 但如果当前 tick 还未抵达 i，此时根据对 f_{o} 的初始化定义为 0，则所有高于 i tick 的区间的 fee 统计尚未产生，为 0。

同样对于 f_{b}——

• 如果当前 tick 抵达或者超过了 i，f_{o}(i) 表示累计到 i 的手续费，也即对所有低于 i tick 的区间的 fee 统计；

• 如果当前 tick 还未抵达 i，对所有低于 i tick 的区间的 fee 统计值即为当前的全局变量 f_{g}（当前总手续费）。

通俗来概括，系统算法要统计某一个 range 内累计的手续费，

• 如果当前 tick 已经处于 range 内部，即 i_{l}\leq i_{c} < i_{u}，只需要从全局手续费 f_{g}减去所有低于 i_{l}组成的 range 累计的手续费；

• 如果当前 tick 不处于 range 内部，且低于下界 i_{l}，说明尚未在 (i_{l},i_{u}) 区间内产生交易，也就未产生手续费，因此该 range 内累计量为 0；

• 如果当前 tick 不处于 range 内部，且高于上界 i_{u}，需要从全局总量中分别去除“两头”各自的累计量，即从全局 f_{g}中减去所有低于 i_{l}区间累计量，再减去“从 i_{u}到当前 tick 区间累计量”。

Uni V3 计算手续费的过程是一种从微观走向宏观的思想，它将空间划分成离散的，每一个时间刻度只会在一个离散空间上产生交易，从而产生手续费，每一个微观 tick 都在各自记录着自己从最低 tick 到自身这段区间内的累计手续费总和，然后供上述公式不断调用，以计算各种宏观结果。

Uni V3 已经改变了传统 AMM 对 LP 行为的设定，也不再基于全局流动性（Global Liquidity）和份额（Share）来为每一个 LP 计算手续费收益。对 V3 来讲，它只关注在每一个 tick 里存在多少“虚拟”流动性，以及这些虚拟流动性产生了多少手续费，算得单位虚拟流动性对应的手续费值；在这个时空之下，我们再把视角切到具体每一个 LP 上，对于任何 LP，都会存在一个“开仓”（Position）的区间设定，他在自己设定的区间提供了虚拟流动性，可能是一个 tick，也可能是连续多个 tick，从最简单的“一个 tick”角度解释，系统会记得同一时空下每一个 LP 在此 tick 注入的虚拟流动性值，并为他们确定出一个比例（注意这个比例只与最开始注入的虚拟流动性大小有关，并不涉及手续费转流动性，这与 V2 是不同的），以此分得该 tick 内所有手续费累计。

在实际情况中， LP 们还会存在复杂的行为，比如注入 / 退出的时间纷杂、选择的 range/tick 纷杂。但 Uni V3 的大道至简之处正是利用全局计算来屏蔽掉单个 LP 视角，只关心 ticks 视角和 Position 视角。在确定好上述所述的一系列全局状态变量的定义后，认真记录好每一笔 swap 交易在 ticks 中发生的情况（包括只在一个 tick 内完成该笔 swap 交易，和需要跨多个 tick 才能完成该笔 swap 交易），同时只记录每个 tick 内虚拟流动性的大小，以此为根本去提供 swap 交易公式以及 swap 后手续费如何分配给参与该 tick 的所有 LP 们。LP 的复杂行为体现在空间的不连续性和时间的不统一性两方面，对于时间不统一性（即会出现很多 LP 不断加入和退出流动性），Uni V3 还会引入 Position 这一级别的全局变量为每一个身份（address）记录下其对 range/tick 加入 / 退出（“setPosition”）时手续费的统计（uncollected fee/feeGrowthInside），确保后来的 LP 不会参与到前序 LP 们已经累计的收益分配。

如果总结来讲 ，tick-level 是对空间上发生的统计，确保起点一致的 LP 们 fee 分配，而 Position-level 是对时间上发生的统计，确保不同起点的 LP 们 fee 累计起点不一样。建议实现者深入 V3 代码，才能真正获得安全计算法。

最后，Uni V3 过于复杂，但大道至简，即便去模仿，模仿者依然需要下功夫深刻了解其“微积分”思维。这篇文章只选择了 fee 这一个角度呈现 Uni V3 的“数学原理”，也是其实现集中流动性的核心逻辑。而在数学之外，我们有更多惊喜的“哲学意义”发现与大家分享，例如 LP token 的进化、NFT 其实并不只属于艺术领域（更有助于金融）、V3 会存在一个策略博弈、V3 对基金池 / 合成资产的启示等等，当然也包括与 MOV 超导 V2 的“心有灵犀”——AMM 的本质是连续性的无限网格，Uni V3 是在这个无限网格基础之上再实现了微观无限网格，是“无数网格机器人的叠加”，MOV 超导 V2 则是在无限网格基础之上进行了更为宏观的无限网格，是超级网格。请期待下一篇《Uni V3 的自然哲学》。