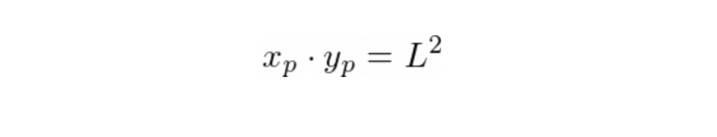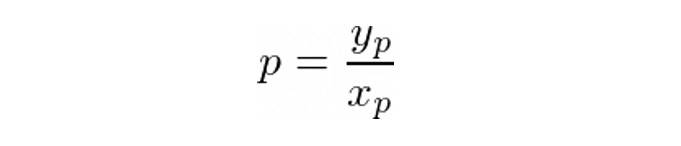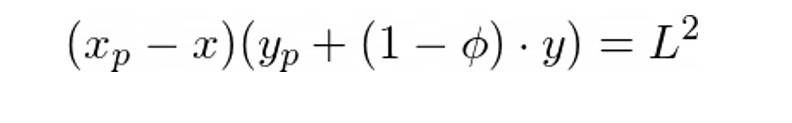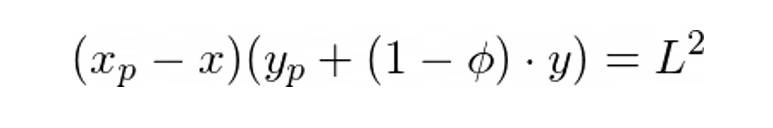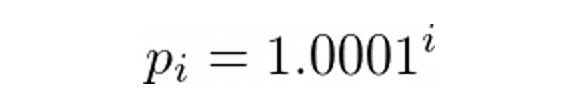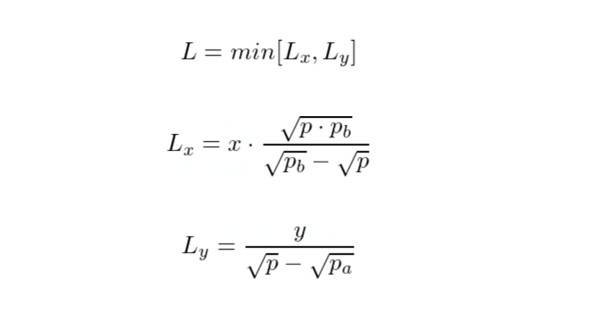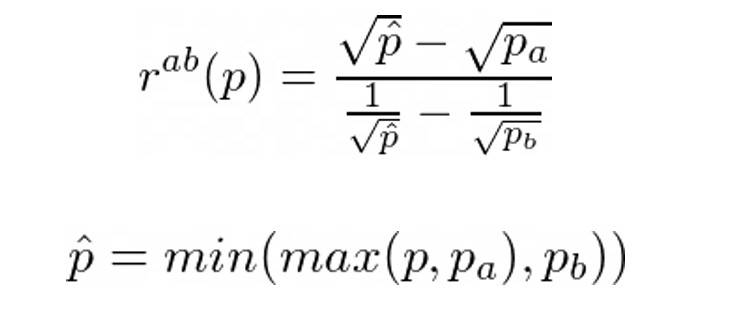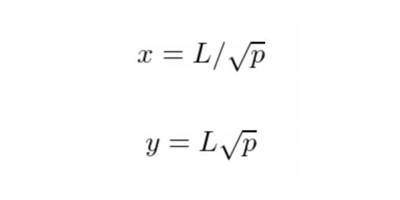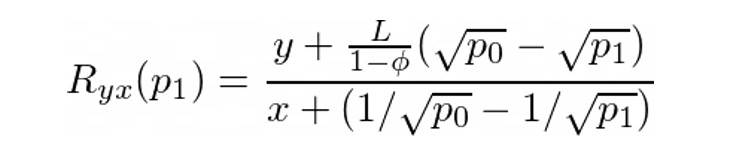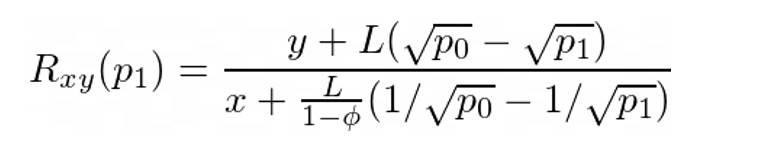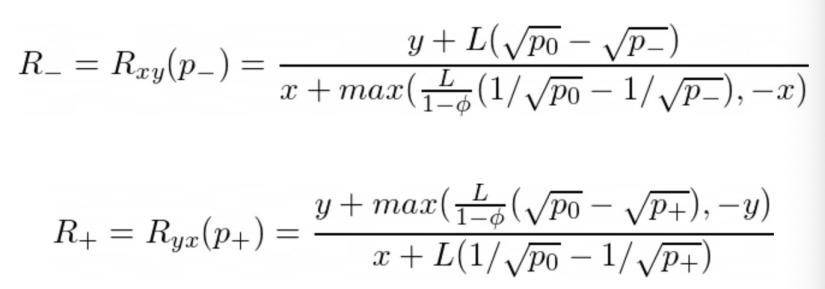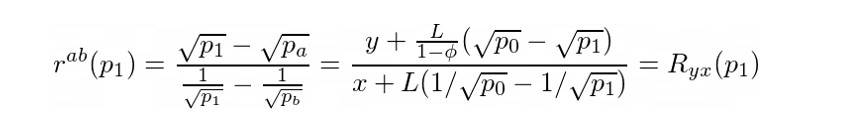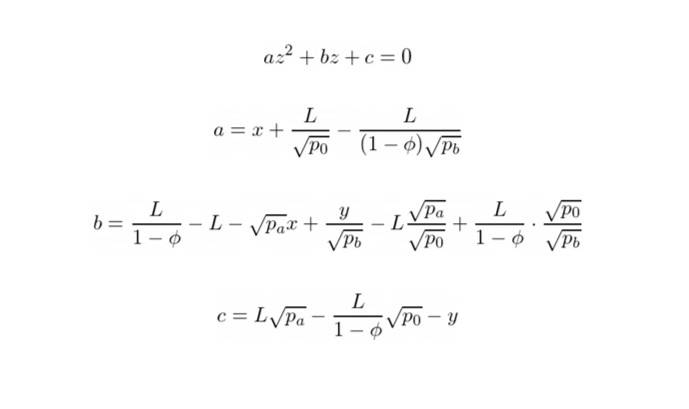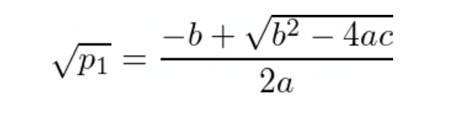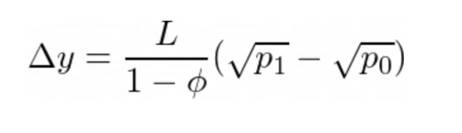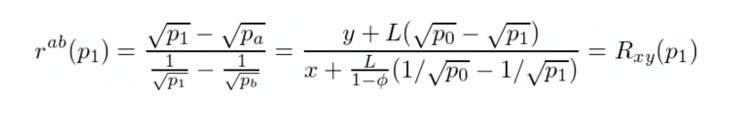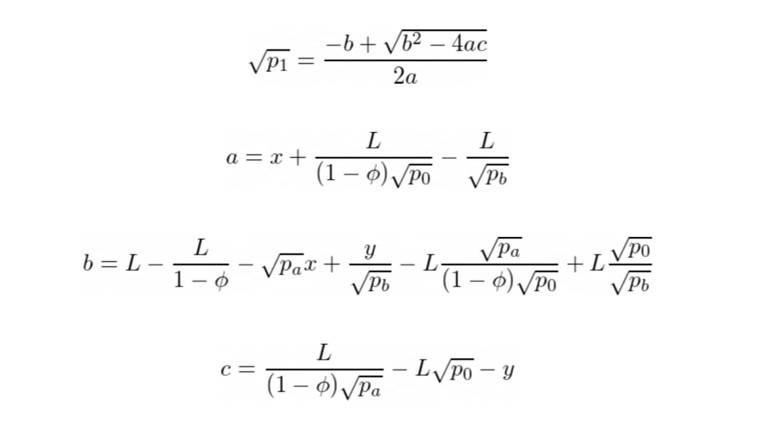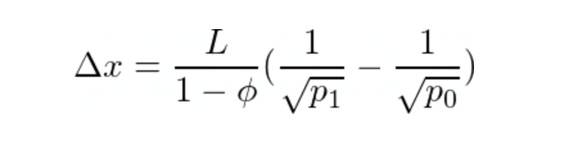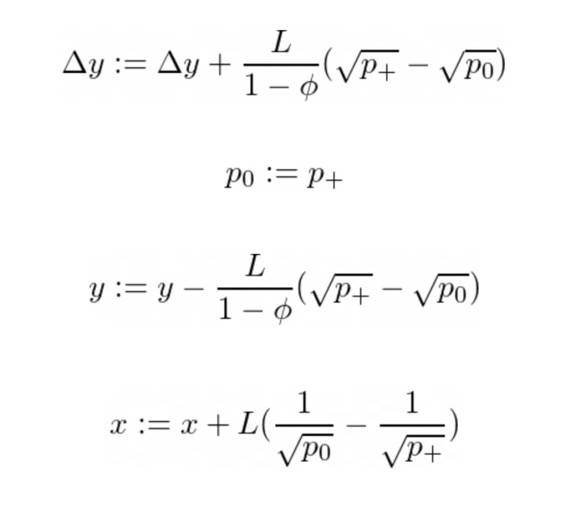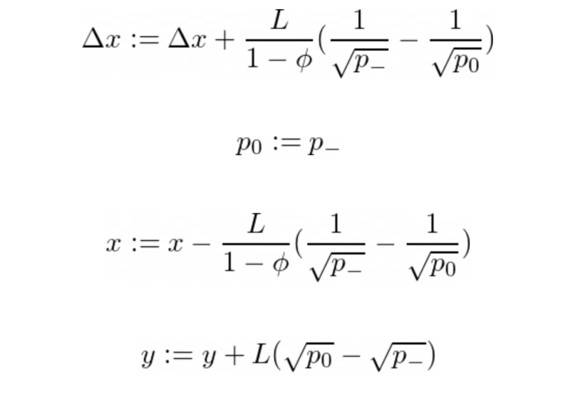在 Uniswap V3 中以正确的比例提供流动性需考虑很多因素,例如刻度间隔内的不同流动性值及如何使用池数据来计算需要交换的代币数量。
撰文:Mellow Protocol
编译:Blake
大家好,客套话就不说了,让我们谈谈 Uniswap V3 的数学逻辑吧!
我们将深入探讨 Uniswap V3 中流动性供应的工作原理,以及如何调整两种代币的投资组合,以便您产生最大的 LP 头寸,同时将 IL 降至最低。接下来会有很多的公式和数字。
Uniswap V2 回顾:交易者的角度
Uniswap V2 是一个自动化的做市商,它允许:
- 交易者将一种资产换成另一种资产;
- 流动性提供者 (LP) 提供流动性并赚取交易费用。
每个池有两种代币:X 和 Y。如果池内有 X p 个 X 代币和 Y p 的 Y 代币(也称为池储备),则池流动性 L 定义为:
当前池中代币的比例定义了当前的交换价格 p:
如果交易者想要交换 y 个 Y 代币,他们将 y 个代币存入池中并收到 x 个 X 代币。 x 由池使用以下等式决定:
这里的ϕ是池费。对于 Uni V2 来说,它的数值是 0.3%。
现在假设当ϕ= 0 时,让我们看看如果当前价格 p = 1,池储备 X p =1,Y p =1,并且交易者想要交换 y= 1 个单位的 Y 代币会发生什么。
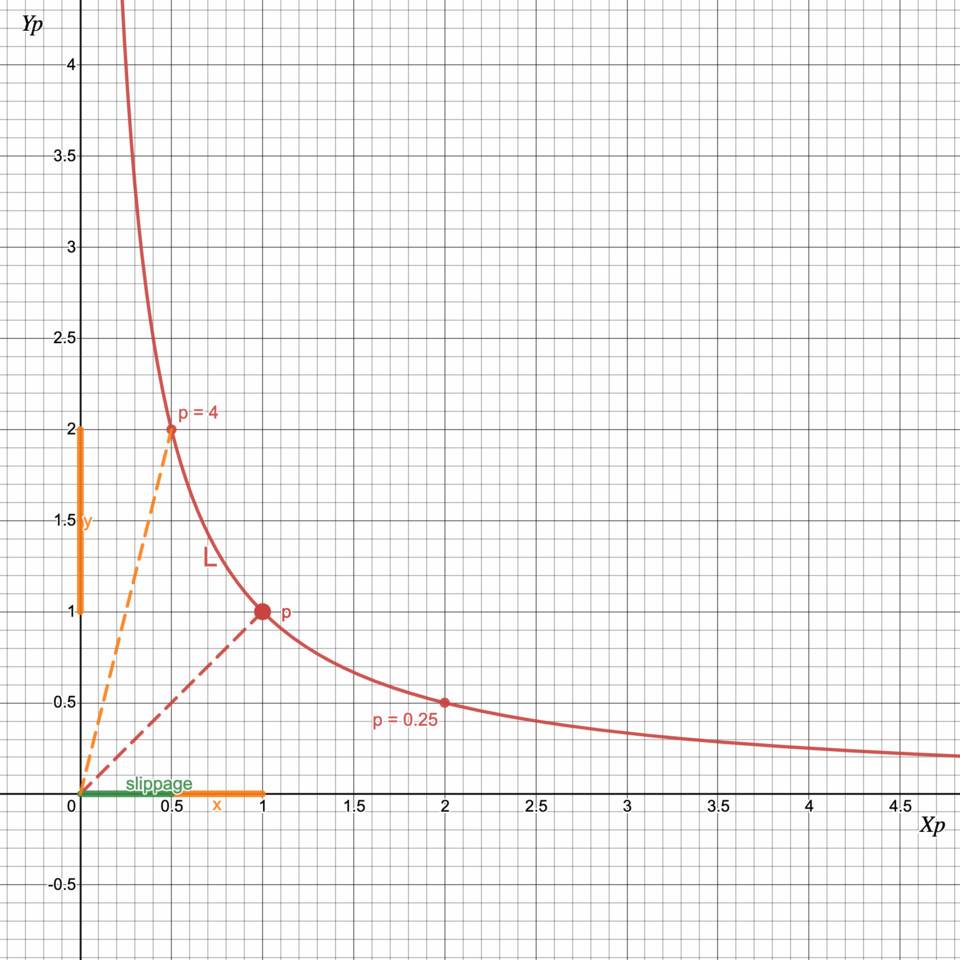
交易者将收回 X 的 x = 0.5 代币。池储备和价格将更新为 X p = 0.5, Y p = 2, p = 4。
我们预计当前价格 p = 1 时 x = 1,但实际 x 金额会受到损失,我们称之为滑点(sl= 0.5):
好消息是 sl→0,因为池流动性 L 增加或交换量减少,即对于足够小的交换量,您以价格 p 交换的费用较小。
Uniswap V2 回顾:流动性提供者的角度
现在让我们看看如果 p = 4,池准备金 X p = 0.5,Y p = 2,L = 1 并且流动性提供者想要放置 x = 0.25 的代币 X 和 y = 1 的代币 Y 会发生什么。
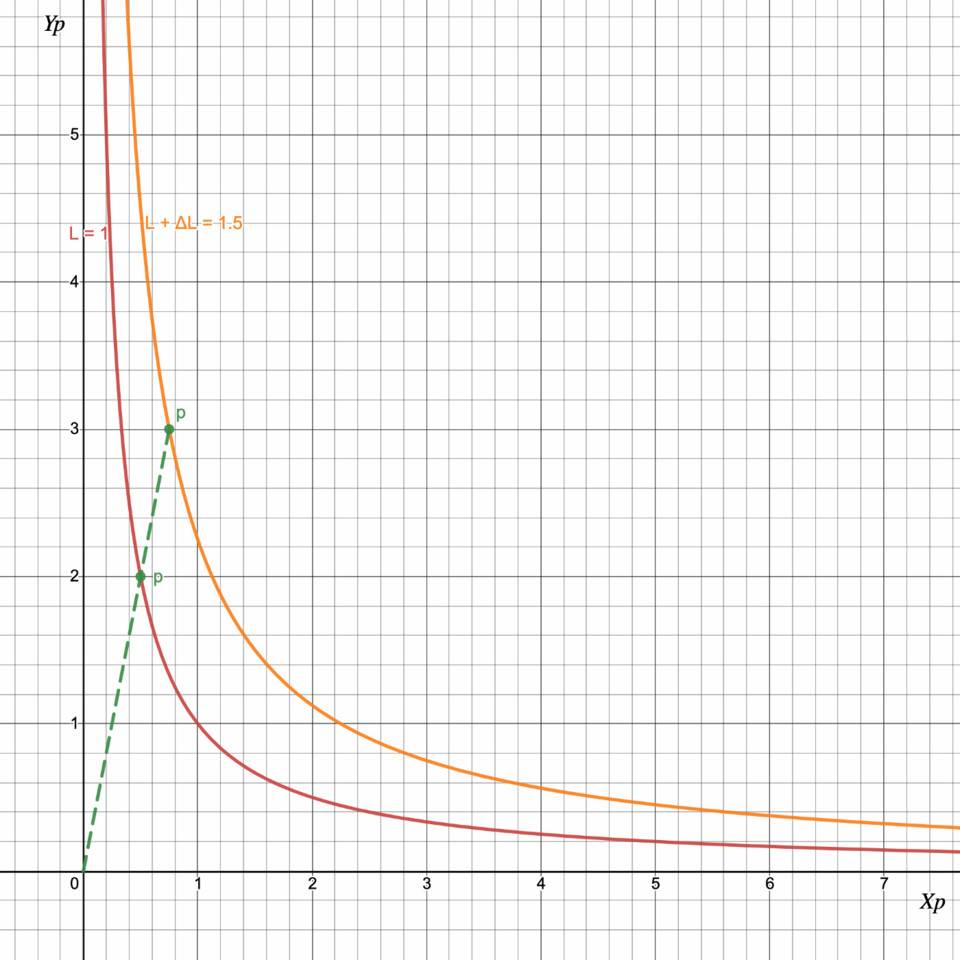
在这种情况下,池的新储备将为 X p = 0.75、Y p = 3 和 L² = X p ·Y p = 2.25,因此 L = 1.5 并且流动性提供者以 Uni V2 lp 代币的形式收到 ΔL = 0.5 的流动性。现在,在每笔交易中,流动性提供者将收到ΔL/L=1/3 份额的费用。
在这个例子中,我们故意使用 x = 0.25 和 y = 1 作为流动性提供者的投资,因此 y / x = 4 = p。
如果 y / x≠p 会发生什么?在这种情况下,一部分代币Δx 或Δy 会被返还给流动性提供者,使得剩余比率 (y-Δy)/ x = p 或 y / (x-Δx) = p。如果流动性提供者想要充分利用他们的代币并获得最大的流动性,他们首先必须交易他们的代币,以便 y / x = p 然后将它们放入池中。
对于 Uni V2,调整您的代币组合以获得最大流动性非常简单。 Uni V3 会怎么样呢?事实证明这越来越复杂。
Uniswap V3:单仓
2021 年 5 月,Uniswap 团队推出了 V3。在 Uni V3 上,您可以将流动性置于任何价格区间 [pᵃ, pᵇ]。只要价格在 [pᵃ, pᵇ] 范围内,您就有流动性 L 并赚取费用。当价格超出范围时,您不会赚取任何费用,直到价格回到范围内。
让我们看看它是如何运作的。首先,让我们考虑只有一个持仓且价格区间为 [pᵃ, pᵇ] = [0.25, 4] 的矿池。当前池准备金为 X p = Y p = 0.5,价格为 p = 1。在这种情况下,随着交换发生且价格在变动,我们观察到以下池行为:
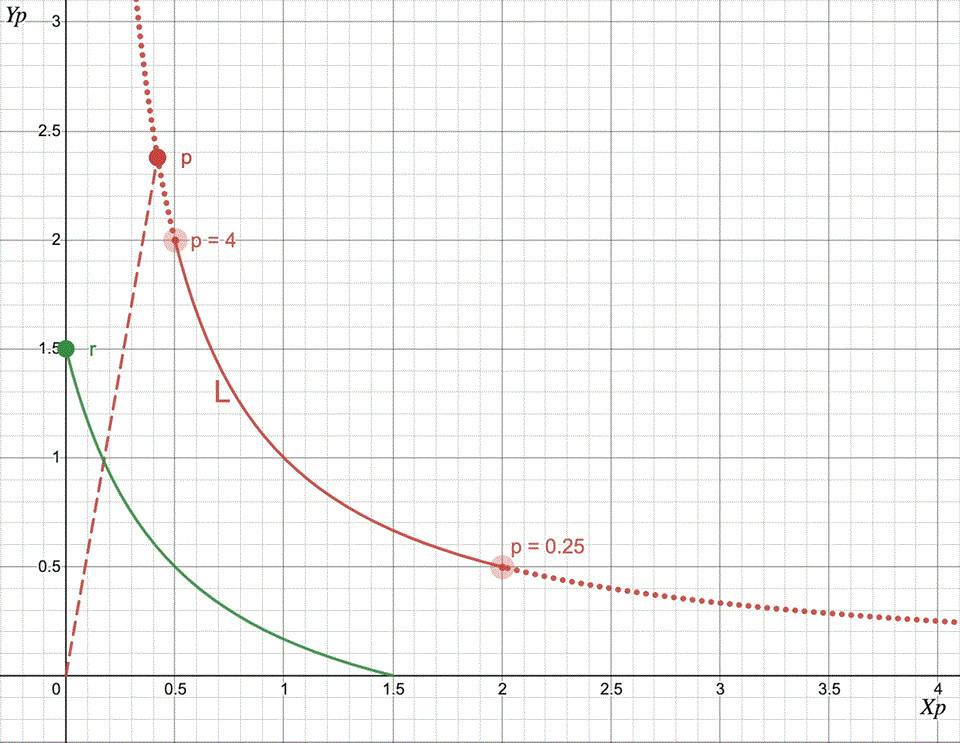
这里绿色曲线是用于交换的实际代币储备(真实流动性曲线),红色曲线是虚拟流动性曲线,模拟用户在 Uni V2 上进行交换。
只要价格在 [0.25, 4] 范围内,池的行为就与拥有红色流动性曲线的 UniV2 池完全相同。当价格越界时,虚拟流动性降至零,实际流动性集中在 X 或 Y 代币中,不用于交换。
Uniswap V3:多仓
现在让我们看看如果在 [pᵃ₁, pᵇ₁] 上有两个流动性投资 x₁, y₁和在 [pᵃ₂, pᵇ₂] 上有 x₂, y₂会发生什么。这些投资中的每一个都意味着(我们将在后面的章节中看到)虚拟流动性 L₁和 L₂
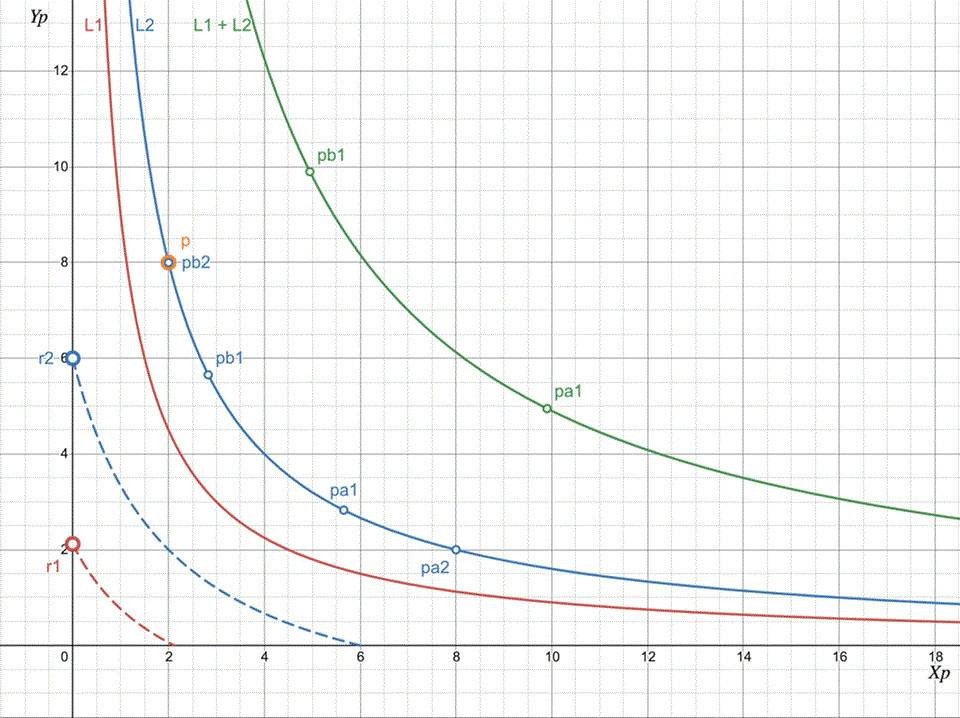
可以看出,当两个区间都覆盖价格时,两个实际储备都被使用,池虚拟流动性等于流动性总和。当只有一个区间覆盖价格时——仅使用其流动性。当价格在两个区间之外时,池流动性为零(或者您不赚取任何费用)。
这为 Uni V3 提供了一个独特的特点——分段流动性函数。当价格沿着虚拟曲线移动时,流动性价值在某些价格点(即流动性头寸的边界)上变化了一些 ΔL。您可以在图 3 中看到在价格 pᵃ₁ 和 pᵇ₁ 处发生这种跳跃。
刻度和刻度间距
Uniswap V3 的实际情况比上图中显示的要困难一些。在真正的 Uni V3 中,您不能将流动性置于任意价格区间。取而代之的是,所谓的刻度在价格范围内形成了一个离散的网格。刻度由公式定义(i 是整数):
对于每个池,还有一个刻度间隔的概念。刻度间距是刻度之上的另一个网格,它限制了您可以放置流动性的刻度。例如,对于 0.3%-费用的池刻度间隔是 60,这样你可以只在每个 60 的刻度上放置流动性,例如,0, -60, 60, 120, -120, ... 下图显示了刻度间距刻度(橙色)和刻度(黑色)
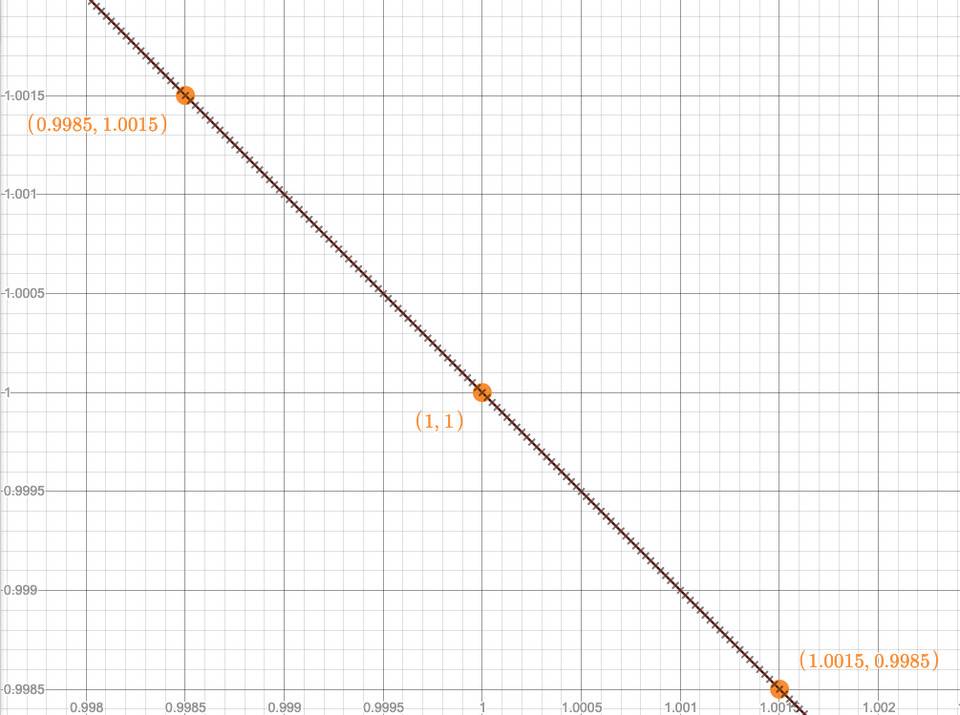
因为您的流动性价格区间界限只能是刻度间距刻度,所以任何空间刻度间隔内的流动性都是恒定的,并且只有在价格穿过刻度间距刻度时才会改变。
因此,我们有一个分段流动性函数,其中可能在刻度间隔刻度处发生跳跃(类似于图 2)。
仓位的流动性价值
让我们看看流动性 L 是如何计算的,给定初始代币 x 和 y、价格区间 [pᵃ, pᵇ] 和当前价格 p。
从这些等式中可以看出,如果 x 和 y 代币的比例不正确(Lx≠Ly),则一些代币将返回给流动性提供者。这与我们在 Uni V2 中观察到的行为类似。
但是对于 Uni V3,它更复杂,因为我们有分段流动性函数,在刻度间隔刻度处跳跃。在下一章中,我们将展示如何在 Uni V3 上以最有效的方式放置代币。
有效的流动性提供
如果我们有一个由 x 个代币 X 和 y 个代币 Y 组成的投资组合,并且我们想为价格范围 [pᵃ, pᵇ] 提供流动性,我们应该交换多少代币 X 或 Y 以从中获得最大的流动性?
为了回答这个问题,让我们用 R = y / x 来表示——我们投资组合中代币的比率和 rᵃᵇ(p)——最佳代币比率,使得 Lx = Ly。从 Lx 和 Ly 的公式我们可以得出:
所以我们的目标是使 R = rᵃᵇ。
然而,这项任务比仅仅将 x 和 y 对齐到指定的比率 rᵃᵇ 稍微复杂一些。当我们开始将 x 交换为 y 或反之亦然时,池价格 p 开始变化,rᵃᵇ 也是如此。这种行为如下图所示:
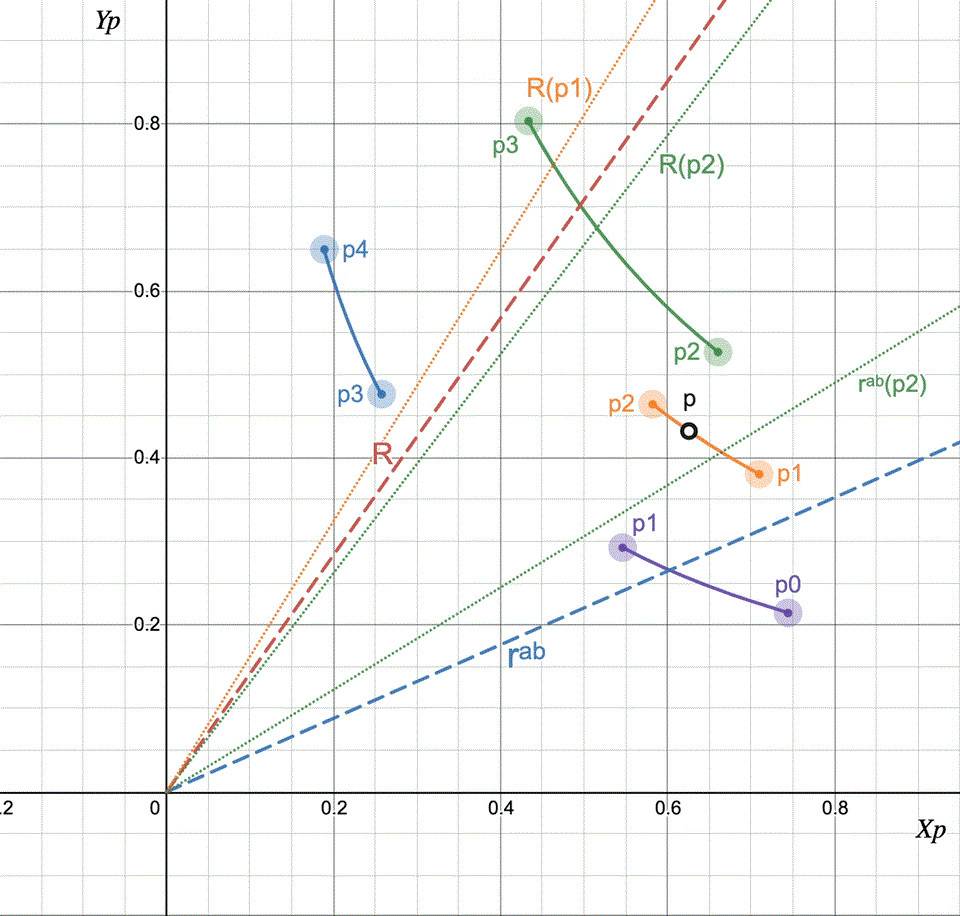
另一层复杂的是,随着价格 p 的变化以及跨越分时间隔分时池流动性 L 也在变化!为了解决这个问题,让我们首先了解在流动性 L 不变的情况下,当我们用代币 Y 交换代币 X 时,比率 R 如何演变。
从方程 L²=xy 和 p = y / x 很容易推导出:
因此,如果我们用 Y 交换 X,从 Y 中减去费用,交换后的价格结算为 p₁ (p₁ > p₀):
如果是用 X 交换 Y,则 p₁< p₀,我们有:
下一个问题是:
R 在什么比率时会穿过刻度间隔以及产生流动性变化?
如果我们将 R+ 表示为穿越上刻度的比率,R- 表示下刻度的比率,p₀是初始价格,p-、p+ 是各自在刻度上对应的价格,L 为刻度间隔的当前流动性,然后我们得到:
最后,我们已准备好解决问题。
首先,我们需要回答 2 个问题:
- R > rᵃᵇ(p₀) 吗?如果是,我们需要将 Y 交换为 X,否则的话将 X 交换为 Y。
- 当我们交换时——矿池价格会跨越一个刻度间隔刻度吗?如果否- 我们可以立即解决问题。如果是-我们需要调整我们的值,就像我们一直交换到刻度间隔,然后在新的流动性上重复我们的算法。
这些问题的答案将我们带到了 4 个不同的案例中:
- 在一个刻度间隔内用 Y 交换 X:R > rᵃᵇ(p₀), R+ ≤ rᵃᵇ(p+)
- 在一个刻度间隔内用 X 交换 Y:R < rᵃᵇ(p₀), R- ≥ rᵃᵇ(p-)
- 在不同的刻度间隔中用 Y 交换 X:R > rᵃᵇ(p₀), R+ > rᵃᵇ(p+)
- 在不同的刻度间隔中用 X 交换 Y:R < rᵃᵇ(p₀), R- < rᵃᵇ(p-)
情况 1:在一个刻度间隔内用 Y 交换 X:R > rᵃᵇ(p₀), R+ ≤ rᵃᵇ(p+)
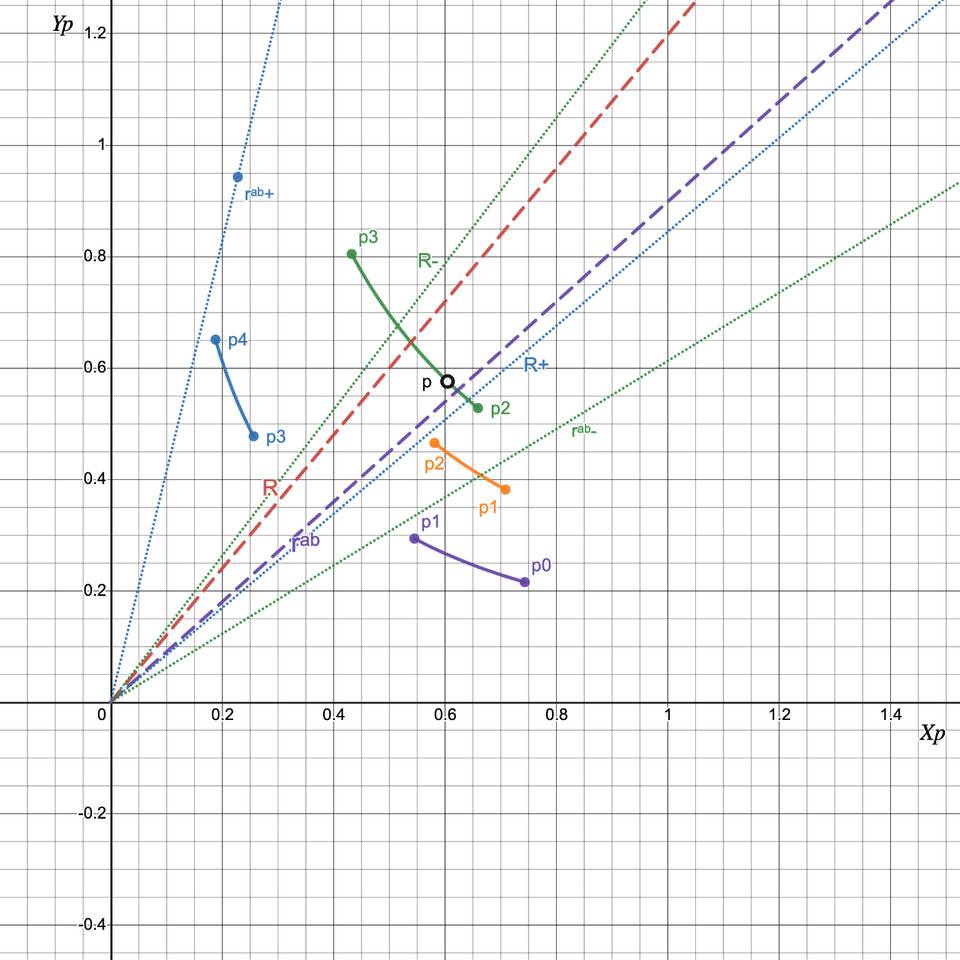
如果我们用 y 交换 x 并且交换后的价格稳定在 p₁,我们只需要确保 Ryx(p₁) = rᵃᵇ(p₁):
如果我们假设 z = √p₁ 并重新排列方程的项,我们将得到一个二次方程:
因此我们可以求解它并找到 p₁:
要交换的代币 Y 的数量是:
情况 2:在一个刻度间隔内用 X 交换 Y:R < rᵃᵇ(p₀), R- ≥ rᵃᵇ(p-)
图 8:在一个刻度间隔内用 X 交换 Y。当我们从 X 交换到 Y 时,价格下降到 p₂,R 增长到 R-,而 rᵃᵇ 下降到 rᵃᵇ-。由于最初 R < rᵃᵇ 并且 R- ≥ rᵃᵇ- 可以保证 R = r 在刻度间隔内。
这种情况与情况 1 非常相似,除了我们是将 X 交换为 Y,因此我们需要确保 Rxy(p₁) = rᵃᵇ(p₁):
与情况 1 类似,我们可以得到:
要交换的代币 X 的数量是:
情况 3:在不同的刻度间隔中用 Y 交换 X:R > rᵃᵇ(p₀),R+ > rᵃᵇ(p+)
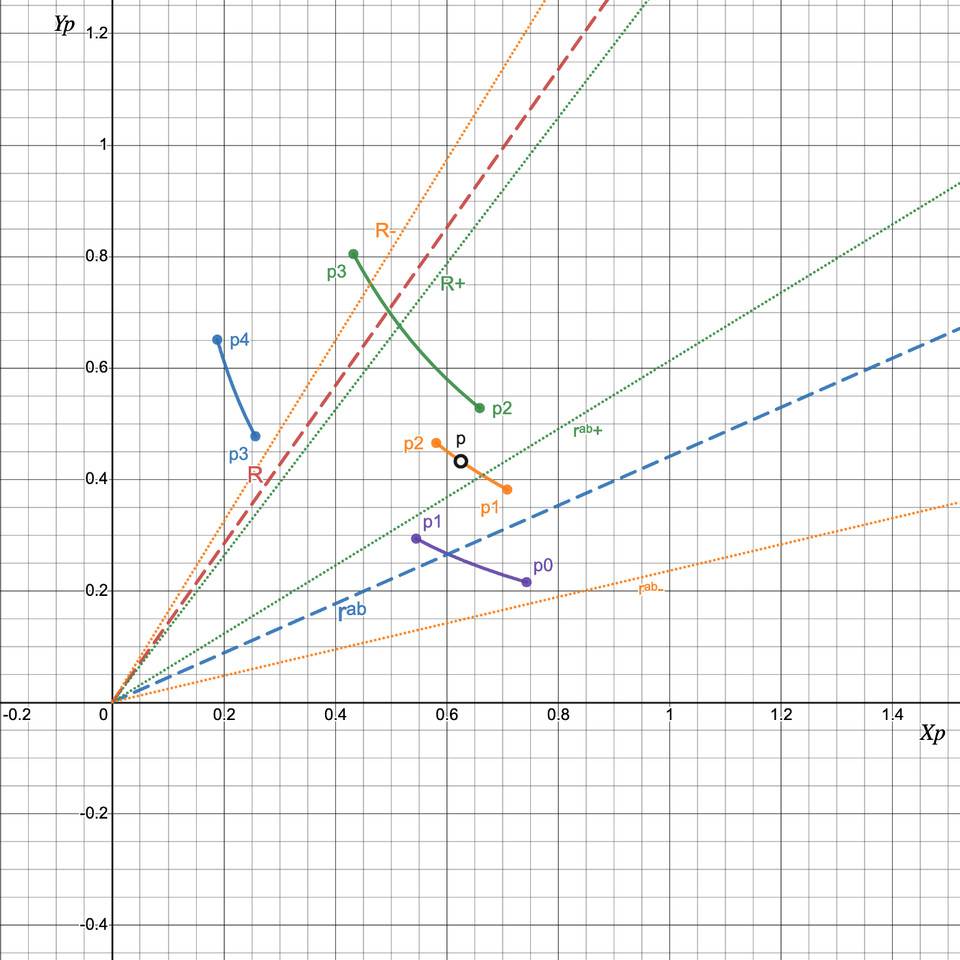
在这种情况下,我们将 Y 交换为 X,直到 R = R+ 并且 p = p+ 并且我们处于具有新流动性的新刻度间隔中。我们记得我们交换了多少个 Y 标记,以便稍后将它们添加到最终数字中。然后我们重新开始算法并重复,直到我们遇到案例 1。 那我们就重新定义:
情况 4:在不同的刻度间隔中用 X 交换 Y:R < rᵃᵇ(p₀), R- < rᵃᵇ(p-)
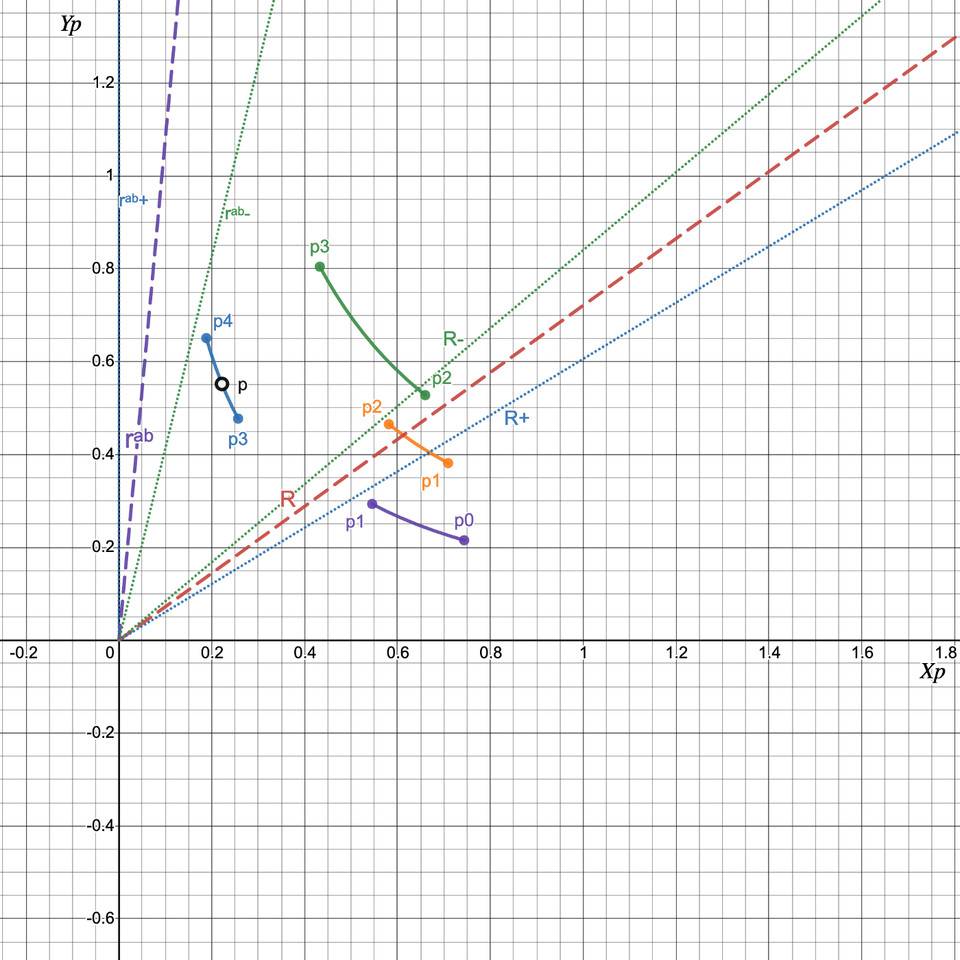
与情况 3 完全相似,除了我们将 X 交换为 Y,直到 R = R- 并重复直到我们遇到情况 2。我们重新定义:
结论
在 Uni V3 中以正确的比例提供流动性是一项非常复杂的任务。您需要考虑很多因素,例如刻度间隔内的不同流动性值。上面的算法描述了如何使用池数据来计算需要交换的代币数量以获得最高的流动性。
数字图表可在此处获得:
https://www.desmos.com/calculator/rqbrnapxbj
https://www.desmos.com/calculator/ys7kcfgjxe
https://www.desmos.com/calculator/ehdwkbtu7z
在以后的文章中,我们计划讨论 Uni V3 的其他有趣方面,如无常损失、多头投资组合、策略风险等。
Mellow Protocol 正在探索 AMM 的流动性提供和做市空间。您还可以在 此处
查看我们的初步研究论文。 Mellow 的目标是建立一个强大的工具生态系统,以消除市场低效率并为用户创造成果。
我们不仅将其视为一种产品,而且将其视为复杂数学可以为 DeFi 领域带来的演变。与 Uniswap 和 Curve 创新用户交易体验的方式类似,我们相信 LP 优化也在推动 tradfi 的可能性。
在接下来的文章中,我们将讨论有关如何实施适当的再平衡策略的更多想法,并将继续讨论 DeFi 中更广泛的主题。