别废话，就问你：比特币会归零吗?

“本文谨献给优秀的华裔量子物理学家张首晟教授。”

比特币发展至今已历经十年，“十年之前，我不认识你，你不属于我”，那么，十年之后，我们和比特币还是不是朋友?还是不是可以问候?还是那种温柔再也找不到拥抱的理由了呢?

这段时间，很多朋友来问比特币会不会归零的问题。其中不乏高位入场的朋友，也有认为跌了差不多了想入市的新人，也有纠结在关机还是坚持挖矿两难之中的矿圈朋友。

前两天一直在写《Web3.0：能否开启未来10年创新创业创富的大门》文章，完成后发现有必要写篇文章讨论下这个话题。

无论是链圈、币圈还是矿圈，有很多充值比特币信仰的文章。但笔者发现，很少有从比特币的白皮书和算法层面来解释的，本文希望能填补上这块。

本文将分四部分：

第一部分，解读《密码朋克宣言》与比特币白皮书。

没有密码朋克运动就没有当代基于密码学的各种点对点网络产品与算法突破，更不用说比特币。解读《密码朋克宣言》对正确理解比特币的产生原因非常重要。其次，解读比特币白皮书的文章有很多，但似乎没有看到过对中本聪这篇论文的开头简介部分和结尾的结论部分做深度刨析的。搞学术的朋友都知道，这两部分常常是最重要的画龙点睛部分。不深刻解读这两部分，很可能会片面的理解比特币。

第二部分，解读比特币的自治机制。

笔者曾解读源码并推导出了一个非常简单的比特币挖矿成本公式，由此公式推导出了基于比特币自治机制的分布式商业理论。这部分将根据这个公式来解读为什么比特币能成为打不死的小强。

第三部分，谈谈支持比特币价格上涨的7个理由。

第四部分，谈谈比特币可能归零的几个条件。

因为篇幅关系，以上四部分将分为两篇文章讲述。

以下是正文：

01

起源与原理

1993年发布的《密码朋克宣言》篇幅不长，提出的核心诉求是如何在互联网上保护用户隐私。以下文字摘自此《宣言》：

由于我们渴望隐私，我们必须确保交易各方只知道该交易需要的信息。既然任何信息都可以被提及，我们必须确保尽可能少地披露。

在大多数情况下，个人身份并不重要。当我在商店里买了一本杂志，然后把现金交给店员时，就不需要知道我是谁了。当我要求我的电子邮件提供者发送和接收信息时，我的提供者不需要知道我在对谁说话，我在说什么，或者其他人对我说什么;我的供应商只需要知道如何在得到商品，以及我欠他们多少钱。当我的身份被交易的潜在机制暴露时，我就没有隐私了。我不能选择性地暴露我自己;我必须始终在暴露我自己的同时，保护我的隐私。

因此，开放社会中的隐私要求匿名交易系统。到目前为止，现金一直是主要的此类系统。

匿名事务系统不是秘密事务系统。匿名系统授权个人在需要时和仅在需要时披露其身份-这就是隐私的本质。

在开放社会中，隐私也需要加密。如果我说了什么，我只想让我想听的人听到。如果我的演讲内容可以向全世界公开，我就没有隐私了。加密表示对隐私的渴望，而用弱加密表示对隐私的渴望不大。此外，在默认为匿名的情况下，要想安全地显示身份，需要加密签名。

我们这些密码朋克致力于建立匿名系统。我们用密码学、匿名电子邮件系统、数字签名和数字货币来捍卫我们的隐私。

密码朋克积极致力于使网络更安全，保护隐私。让我们一起赶紧行动，团结起来!

这份25年前的《宣言》明确提出了：要用数字签名和数字货币来捍卫隐私。

这也可以看作是密码朋克运动的使命之一。1993年之后，该组织中的重要人物 Wei Dai、David Chaum、Adam Back、Nick Sazbo、Hal Finney等人在数字货币技术上相继做出了非常杰出的探索，最终2008年由中本聪集大成，推出了点对点网络上的电子现金系统解决方案，即：比特币。

接下去来看比特币白皮书的简介，内容如下：

互联网上的贸易，几乎都需要借助金融机构作为可资信赖的第三方来处理电子支付信息。虽然这类系统在绝大多数情况下都运作良好，但是这类系统仍然内生性地受制于“基于信用的模式”(trust based model)的弱点。我们无法实现完全不可逆的交易，因为金融机构总是不可避免地会出面协调争端。而金融中介的存在，也会增加交易的成本，并且限制了实际可行的最小交易规模，也限制了日常的小额支付交易。并且潜在的损失还在于，很多商品和服务本身是无法退货的，如果缺乏不可逆的支付手段，互联网的贸易就大大受限。因为有潜在的退款的可能，就需要交易双方拥有信任。而商家也必须提防自己的客户，因此会向客户索取完全不必要的个人信息。而实际的商业行为中，一定比例的欺诈性客户也被认为是不可避免的，相关损失视作销售费用处理。而在使用物理现金的情况下，这些销售费用和支付问题上的不确定性却是可以避免的，因为此时没有第三方信用中介的存在。 所以，我们非常需要这样一种电子支付系统，它基于密码学原理而不基于信用，使得任何达成一致的双方，能够直接进行支付，从而不需要第三方中介的参与。杜绝回滚(reverse)支付交易的可能，这就可以保护特定的卖家免于欺诈;而对于想要保护买家的人来说，在此环境下设立通常的第三方担保机制也可谓轻松加愉快。在这篇论文中，我们(we)将提出一种通过点对点分布式的时间戳服务器来生成依照时间前后排列并加以记录的电子交易证明，从而解决双重支付问题。只要诚实的节点所控制的计算能力的总和，大于有合作关系的(cooperating)攻击者的计算能力的总和，该系统就是安全的。

从这段文字中可以看出，中本聪开发比特币的初心来源于以下几点：

1、现有的中心化信任机制存在严重缺陷，包括：

交易的可逆性或回滚(Reverse)会给买卖双方造成潜在风险;

中心化的交易中介会增加交易成本;

中心化的交易中介会限制小额支付;

交易双方的隐私得不到保护;

人为控制的信任中介不可靠;

2、比特币需要解决问题，包括：

用密码学构建全新的信任机制，替代人为信任机制;

直接保护卖家免于欺诈;

通过第三方担保机制，间接保护买家权益;

不可逆的记录所有交易，解决“双花支付”;

3、解决方式为：

通过点对点网络上的时间戳服务器来为所有交易排序，确保交易不可逆;

通过公私钥数字签名，构建密码学信任机制;

如果能够证明诚实节点的算力大于有共同作恶企图的攻击者算力总和时，系统安全。

由此可见，比特币解决的问题是：实现用户间不可逆的点对点直接支付。

最后，来看比特币白皮书的结论部分，内容如下：

我们在此提出了一种不需要信用中介的电子支付系统。我们首先讨论了通常的电子货币的电子签名原理，虽然这种系统为所有权提供了强有力的控制，但是不足以防止双重支付。为了解决这个问题，我们提出了一种采用工作量证明机制的点对点网络来记录交易的公开信息，只要诚实的节点能够控制绝大多数的CPU计算能力，就能使得攻击者事实上难以改变交易记录。该网络的强健之处在于它结构上的简洁性。节点之间的工作大部分是彼此独立的，只需要很少的协同。每个节点都不需要明确自己的身份，由于交易信息的流动路径并无任何要求，所以只需要尽其最大努力传播即可。节点可以随时离开网络，而想重新加入网络也非常容易，因为只需要补充接收离开期间的工作量证明链条即可。节点通过自己的CPU计算力进行投票，表决他们对有效区块的确认，他们不断延长有效的区块链来表达自己的确认，并拒绝在无效的区块之后延长区块以表示拒绝。本框架包含了一个P2P电子货币系统所需要的全部规则和激励措施。

在对比特币网络的技术体系做了非常详尽的描述，并且证明了只要防止51%攻击就能有效保障网络安全之后。中本聪做了以上总结，在总结中，他明确说明：

比特币是一种不需要信用中介的电子支付系统(A system for electronic transactions without relying on trust)

其次，他提到了比特币的几项最关键的技术，这些技术也构成了以后区块链的核心技术与思想：

1、工作量证明;

2、只要防止51%攻击就能维护网络的健康，即简单多数好人原则;

3、通过CPU算力投票，获取记账奖励(即比特币)，同时系统内产生新的可流通使用的比特币;

4、最长链原则;

5、弹性的点对点网络，节点自由进出;

通过以上解读，我们可以明确：比特币不是金融传销。相反，他有一套非常科学的算法机制以及不受人为控制的运行机制。

这套运行机制完全通过全球几十万台高性能电脑(矿机)来共同维持，成为一个不可能停摆、交易无法回滚的电子支付系统。

02

自治机制

2.1 挖矿机制

由于没有中心化机构发行比特币，也没有机构为往来交易账目做记账工作，所以必须要设计一套机制，在没有中心化的管理下，通过算法保持不断运行。

中本聪将比特币预先“埋在”比特币区块链上，不被任何人所拥有。所有的节点(矿机)通过算力比拼竞争记账权，竞争记账权的方法是：哈希猜谜。

什么是哈希猜谜呢?

有一种特殊的哈希值，前面会出现N个零，由于哈希算法具有不可逆性，所以只能通过不断的正向加密尝试，才能“猜到”前面会出现N个零哈希值的明文。零的数量越多，需要不断试验的次数越多，也就是难度越大。

算力就是在一秒内能计算这种加密算法的次数。算力越高，猜中的概率越高，拿到记账权的概率也就越高，得到的比特币奖励也就越多。

比特币网络上靠算力比拼，争夺记账权，一旦抢到了某个区块的记账权，就能够得到比特币奖励。这就是比特币的POW共识机制，又称“工作量证明”。

获得比特币奖励的过程称为“挖矿”，购买用于挖矿的专用电脑设备称为“矿机”，通过算力比拼获取比特币的人称为“矿工”。

每隔10分钟左右，比特币网络上会产生一个新的区块。区块中打包了过去10分钟内全网的所有交易记录(严格讲一个区块中的交易记录会受区块链大小限制)，负责为这个新区块记账的矿工将获取或者共同分享12.5个比特币的奖励。按今天的价格(美元3800/BTC)，也就是每隔10分钟，将新增约47500美元的流动性，每天新增流动性近700万美元。每隔四年，这个出块奖励会减半，也就是每天新增的流动性会减半。下一次减半大概在2020年5-6月之间某一天。

2.2 比特币挖矿公式

根据比特币源码中的算法，我推算出以下比特币挖矿公式，即一台算力为H的矿机，一天24小时内不间断工作，能挖多少个比特币：

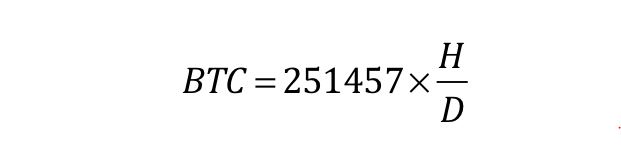
其中H是矿工拥有矿机的算力，D是当前难度。

**公式的推导过程见最后。

以S9矿机为例，一台的算力H=14500G，写此文时的挖矿难度为：5,646,403,851,534

因此，24小时挖矿后，可以得到：0.000645743131个比特币，按$4000元一枚的价格计算，每天约有$2.583的毛收入。

当然，矿机的运行需要电，于是我们有了下面的挖矿净利润公式：

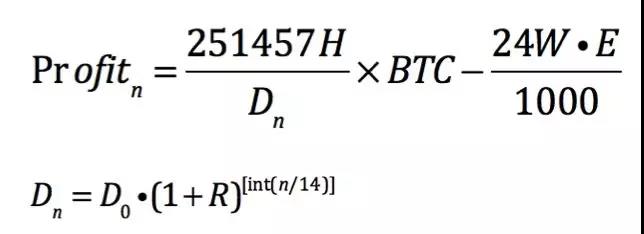
2.3 难度增长

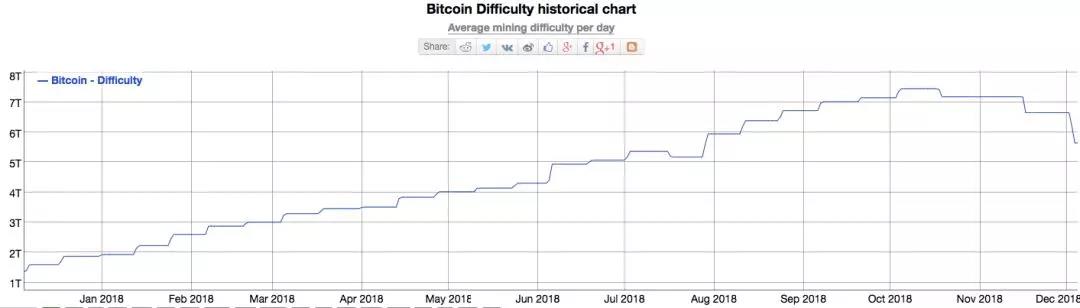
这里有一个非常重要的概念是：难度D会不断增长，一般每14天增长一次。所以对于一台算力固定的矿机，他的收益是逐步下降的。

下图是最近一年内的难度变化图，可以访问网址： https://bitinfocharts.com/comparison/bitcoin-difficulty.html 获取即时的难度数据。

2.4 挖矿盈亏平衡

因为难度的不断增长(最近因为BCH分叉，导致下降)，但是电费等支出是固定的，如果假设价格一定，每台矿机总有一天的产出不够当天的电费等支出。于是我们可以计算出一台矿机能否回本，以及回本时间。

以目前主流矿机S9为例，该矿机的参数如下：

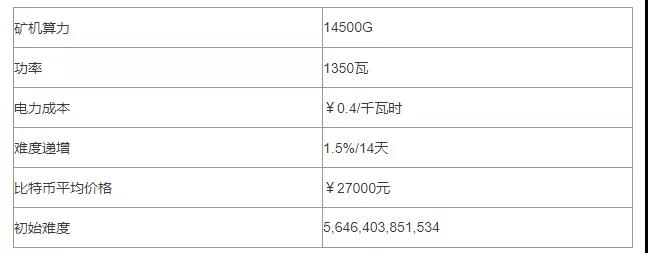
我们可以得到以下净利润图形：

其中横轴是天数，纵轴是累计净利润。

​

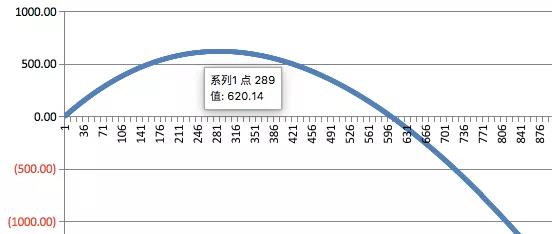
根据上图，我们看到该台设备在289天的时候，最多能收回￥620元，如果过了这个时间点再挖的话，挖到比特币的收益将低于电费支出，曲线开始下降。

￥620元这个价格就是该设备当前的合理价格，也是盈亏平衡点下的设备投资成本。

2.5 自治机制

通过上面公式以及计算，可以看出，当矿工的矿机算力增加时，获得的比特币数量也增加;而当随着大量矿机加入挖矿，也会推动全网难度(D)的提升，难度的提升，又会降低单个矿工挖矿的收益。相反，如果难度(D)降低，则会提高挖矿的收益。这就是比特币自适应机制的精华。

在这个自适应机制下，我们就能理解：为什么比特币价格会被不断推高，为什么比特币在各种风波中仍能生存至今?

首先，随着技术的进步，高算力矿机进入挖矿，试图获取比平均算力更高的算力优势，以获取更多收益。但这些新进入的矿机会迅速把总算力拉升，难度随之飙升，不久，行业内会发现，挖矿并不划算。老的矿机退出，难度增长恢复到正常水平，挖矿的收益又提高了，于是，新的矿机又开始蜂拥而入。

如此反复，比特币的价格就在矿工的一波一波自适应过程中上涨。每次因为外界原因，导致价格暴跌后，都会让很多矿工离场，然后算力和难度下降，等挖矿成本降到与跌下来的价格相平衡的位置时，新的矿机又再一次进入。

比特币就是在这种自适应机制下，从2009年年初一直动态的的运行至今。

以上两部分介绍了比特币的原理和算法，下篇会基于这些基本原理来分析支持比特币上涨的理由以及可能导致比特币归零的风险。

我们下回见!

----

**附：比特币挖矿公式推导过程

Sha-256哈希算法会产生一个256位的二进制数，因此每次“猜谜”的成功概率为【2的256次方-1】分之一，也就是平均需要计算2的256次方 - 1次才能算出。

即：2**256 - 1 = 115792089237316195423570985008687907853269984665640564039457584007913129639935

当难度为D时，需要计算如下次数。(在Python中，**符号代表幂运算)

(0xffff * 2**208)/D

因此总的哈希次数为

D * 2**256 / (0xffff * 2**208)

因为每10分钟产生一个区块，10分钟等于600秒，所以将上面换算成每秒算力：

D * 2**48 / 0xffff / 600

换算成10进制就是：

D * 2**32 / 600

笔者在推导本公式时是2017年8月15日，那天的难度D为：923,233,068,448。

带入上述公式，在该难度下，需要算力：6,608,759,725,949,815,794，即6609P/秒的算力，才能在10分钟内产生1个区块，即12.5个BTC。

也就是需要：6609P / 12.5BTC = 528.72P 的算力才能挖出一个比特币。

S9矿机13.5T/s算力，也就是528720T / 13.5T/s = 39164台机器挖矿，能在10分钟内产生一个BTC。

也就是 39164 / 144个10分钟 = 272台S9矿机，每天能挖一个BTC。

将以上过程整理成公式，设D为难度，H为算力(G为单位)，每天能挖的比特币数量为：

600 * 10**9 * 12.5 * 144 * H / 2 ** 32 / D

将以上公式简化为：

251457 * H / D

推导完毕。

以上推导严格按照比特币源码，实际操作中，时间上会有所延长或缩短，会对公式产生一些的影响，但总体上将保持一致。