DeFi之道丨一文探讨Uniswap V3的最佳做市方案

写在前面：自上线以来，Uniswap V3在短短的几个月里便已跃居去中心化交易所（DEX）交易量的榜首位置，而据数据统计显示，目前多数Uniswap V3 LP仍使用了简单、被动的流动性头寸，这表明Uniswap V3拥有巨大的潜力尚未被挖掘出来。而来自哈佛大学的4位研究者，Michael Neuder，Rithvik Rao，Daniel J. Moroz以及David C. Parkes则撰写论文探讨了Uniswap v3的流动性供应策略，他们得出结论称，在风险中性和低风险情况下，比例重置分配策略几乎是最佳的，而在高风险情况或对于风险极度厌恶的流动性提供者而言，最优的方案就是均匀重置分配。

概述

Uniswap是当前最大的去中心化数字资产交易所，而其最新的版本Uniswap v3允许流动性提供者（LP）将流动性分配到一个或多个资产价格区间，而不是整个价格范围。当资产市场价保持在该区间内时，流动性提供者（LP）获得的奖励与分配的流动性数量成正比。

这引发了流动性提供策略的问题：当价格保持在区间内时，较小的间隔会导致流动性更集中，相应的回报也更大，但风险会更高。我们将这个问题形式化并研究了流动性提供者（LP）的三类策略：（1）均匀分配、（2）比例分配以及（3）最优（通过约束优化问题）分配。

我们展示了基于以太坊历史价格数据的实验结果，这表明简单的流动性提供策略可产生接近最优的效用，在低风险的情况下，它要比Uniswap v2流动性供给收益高出200多倍。

一、简介

去中心化金融（DeFi）是加密货币和区块链生态系统中一个庞大且快速增长的领域，其旨在使用在区块链（通常是以太坊）上执行的智能合约复制传统金融中介和工具并进行金融创新。

从2020年5月到2021年5月，进入DeFi协议的TVL（总锁定价值）已从8亿美元快速增长到800亿美元[15]。

作为DeFi子领域的去中心化交易所（DEX），允许用户在没有可信中介的情况下交换不同类型的代币。而目前多数的去中心化交易所（包括 Uniswap）都属于恒定函数做市商 (CFMM) 类别。CFMM 不像传统交易所那样使用订单簿，而是使用自动做市商 (AMM) 来确定资产的价格。

在 Uniswap v2 中，代币对可使用包含两种代币的流动性池相互交换。允许的交易由储备曲线 ?*? = ? 决定，其中? 和 ? 表示流动性池中每种类型的代币数量，而 ? 在交易中保持不变。流动性提供者（LP）将代币添加到流动性池中供交易者交换，并通过交易者支付的费用获得奖励。图 1（蓝色）显示了Uniswap v2 的储备曲线，为了用一定数量的代币 ? 换取一定数量的代币 ?，交易者必须保持储备的乘积不变，即 (? − Δ?) (? + Δ?) = ? .

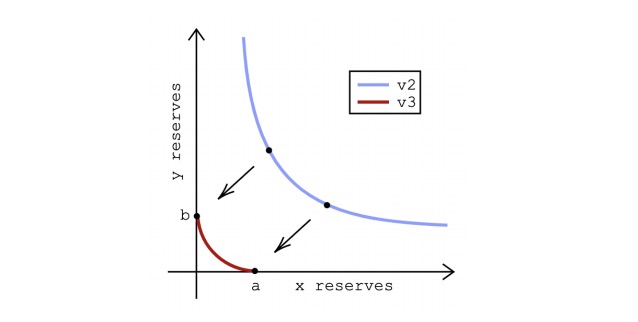
图 1：Uniswap v2 和 v3 的储备曲线。在价格区间 [??, ?? ] 上提供 v3 集中流动性导致 Uniswap v2 曲线 ?*? = ? 分别在 ? 和 ? 处截取轴。通过在 v3 储备曲线（方程 1）中将 ? 和 ? 设置为零来计算截距。

该储备曲线还以代币 ? 为单位定义了代币 ? 的有效价格，即 ?? (?, ?) = −??/?? [12]。在 Uniswap v2 的 ?*? = ? 曲线的环境中，我们有

。

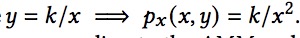
然后，我们将AMM和流动性池对应的“价格”取为?的价格，即??（?，?），我们让?代币相对于?代币具有波动性。在Uniswap v2中，当交易者使用流动性进行swap交易时，流动性提供者就会获得奖励，每次产生 0.3% 的固定费用 [2]。每个流动性提供者在可能价格的整个区间 (0, ∞) 上提供流动性，并根据其占池中总流动性的比例获得奖励。

2021年5月3日，Uniswap的新协议Uniswap v3[3]上线了以太坊主网。Uniswap v3对Uniswap v2的主要更新便是增加了集中流动性[3]。在三周内，这个新协议累积超过 12 亿美元的 TVL，日均交易量达到 16 亿美元 [17]。在 Uniswap v3 中，流动性提供者（LP）可以向任意数量的价格区间（称为头寸）提供流动性。

当价格保持在该区间时，分配给头寸[??, ??] 的流动性会从费用中获得奖励。如果多个流动性提供者（LP）在包含正确价格的间隔内分配了流动性，则每个LP将按其在该价格范围上拥有的流动性比例获得奖励。图 1（红色）展示了 Uniswap v2 的恒定乘积曲线如何移动以截取 ? 和 ? 处的轴，这两个轴由头寸价格区间的上限和下限决定。这个变动曲线 [3] 由下面这个公式给出：

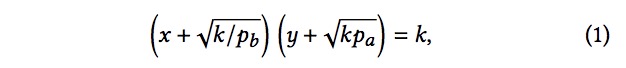
而截距 ? 和 ? 可通过让 ? 或 ? 分别为零来计算。

通过这种方式，Uniswap v3 支持了关于流动性分配的多种策略，而每种策略都存在着不同的权衡。此外，重新分配流动性是有成本的，这涉及到了区块交易，因此会产生 gas 费用，因此这一成本必须被纳入流动性提供者的策略中。

本文的贡献如下：

(1) 将流动性提供问题和一系列流动性提供策略形式化，我们称之为“重置流动性提供策略”（reset-LP 策略）；

（2）为流动性提供者提供三类重置 LP 策略，我们称之为均匀分配（uniform）, 比例分配（proportional）以及最优分配（optimal）；

（3）解析计算重置LP策略的预期效用；

（4）根据以太坊历史价格求解最优重置LP策略；

（5）证明比例分配对于风险偏向LP提供者是最优的，而均匀分配对于风险规避LP提供者是最优的；

（6）对最优重置LP策略进行回测，以证明在适当的条件下，采用该策略的LP提供者将获得比遵循v2策略高200倍的投资回报。

1、1 目录

第2节介绍了Uniswap v3协议，并介绍了流动性供应策略的概念。我们主要关注的是称为“?-reset”的重置策略类。第三节介绍了马尔可夫模型，用于分析这类策略的预期效用。第4节介绍了三种具体的流动性提供策略，包括最优的“?-reset ”重置策略。

第5节介绍了基于以太坊历史价格数据的实证结果。第6节提出了有待进一步研究的问题，并进行总结。

二、关于Uniswap v3

Uniswap v3向AMM引入了集中流动性的概念，流动性提供者（LP）现在可以为提供流动性的资产之一指定一个或多个价格区间，而不是在 (0, ∞) 的整个价格范围内提供流动性。当指定资产的价格在这些间隔之一内（并且只在这个时间间隔内）时，流动性提供者才能赚取到交易费用。此外，如果多个流动性提供者（LP）将流动性分配到相同的价格，则他们每个人将按其拥有的该价格范围的总流动性比例获得奖励。

通过选择更集中的区间，当价格保持在该区间内时，流动性提供者（LP）可以增加他们的回报，但这也会增加回报的差额。为了将其形式化，我们建立了一组离散的价格 bin区间模型，流动性提供者（LP）选择在每个bin区间中放置多少流动性以及何时重新分配流动性。

定义2.1 （Bin）。我们定义了一组bin ? = {?1, ?2, . . . , ??, . . .},其中每个bin ??对应价格区间[?? , ??), 它们形成 [0, ∞) 的分区间，其中?1 = 0 以及 ?? = ??+1 ?, ∈ {1, 2 . . }。Bin ?? 对应区间 [?? , ??)。Bin ??表示包含资产当前价格的 bin区间。

对于这项工作的其余部分，我们是以一种资产的单位衡量代币对的另一种资产。例如，USDC/ETH 这个池子，我们以稳定的 USDC 单位衡量 ETH 的波动价格。考虑时间 ? = ? 并让 ?? 表示包含波动资产当前价格的 bin区间。在时间 ? = ? 的流动性提供策略，提供了一种方法来确定流动性提供者（LP）分配给每个bin区间的流动性比例。

我们做出了以下假设：

（1）稳定价格分布 —— 我们假设下一价格分布，描述价格相对于当前价格的百分比变化在时间上是恒定的。我们使用以太坊10分钟的历史价格数据进行了实证验证，我们发现以下概率分布对之间的相关系数为 ?^2 = 0.98 （i）高于 300 美元的 ETH 价格与低于 300 美元的 ETH 价格 （ii）2018 年 4 月至 2019 年 4 月的 ETH 价格与 2019 年 4 月至 2020 年 4 月的 ETH 价格。

(2)重新分配流动性的固定成本——我们假设重新分配流动性的成本是固定的（固定为 1），其他值相对于该成本进行标准化。例如，如果流动性提供者分配 ℓ = 100 单位的流动性，这被解释为重新分配流动性的成本的 100 倍。

（3）定期更新——我们假设流动性提供者（LP）的流动性分配会定期更新，任何重新分配都会立即生效。此外，我们将周期长度取为足够长（至少 10 分钟），网络传输延迟不是这篇论文要关注的重点。

（4）单一策略提供者——我们假设了一个单一的流动性策略提供者，并隐含地将其余提供者建模为在整个价格范围内分配流动性，即遵循Uniswap v2 流动性提供方法（ 译者评论：实际Uniswap v3环境中存在大量不同策略的LP头寸，因此论文给出的最优策略结果不具参考意义 ）。

2、1 流动性提供策略

在描述流动性提供策略问题时，我们首先定义时间指数?处价格??的随机过程{??：?∈N}。我们对稳定的下一个价格分布进行建模，描述了价格相对于当前价格的变化随时间的推移是恒定的，并且对当前价格也是不变的。

为此，我们相对于当前价格重新索引价格bin区间。让?? 表示当前价格bin区间，并将其相对索引为?(0)。让 ?(−?) 和 ?(?) 分别表示左侧和右侧?? 的第K个bin区间。对于集合?? = {−?max, −?max + 1, . . . , 0, . . . , ?max}，其中?max是最大可能的下一价格变动。根据假设 1，我们可以写出下面这个公式：

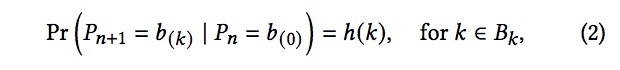
其中 ℎ(?) 是向左或向右移动k个bin区间的概率 。

鉴于此，我们现在可以定义一个简单的流动性提供类别策略。

定义 2.2。 重置流动性提供策略（reset-LP 策略）包括：

（1）重置时包含价格的bin区间，?? = ?(0)

（2）分配 ?(?) ∈ [0, 1]，指定分配给 ?? 中每个 bin区间?(?)的流动性比例。

（3）一个重置条件，它指定了 ? 中导致策略重置的 bin区间子集。重置后，分配规则 ? 用于重新分配流动性，以新价格 ?? 为中心。

特别令人感兴趣的是?-reset重置策略家族。

定义 2.3。?-reset 策略是一种 重置LP策略，其中定义了重置条件，以便仅当价格超出集合 ?? = {?(−?? ) , · · · , ?(0), · · · ?(?? )} 的 2?? + 1 个连续 bin区间时才进行重置。

有时我们也使用 ? 来表示被?? 覆盖的下一价格分布的概率质量。例如，如果 ? = 0.50，那么 ??被选为最小的数字，使得集合 ?? 包含至少 50% 的下一价格概率质量。

我们有时也写 ?? 来表示对应于这组 bin区间的一组相对索引，即 ?? = {−?? , · · · , 0, · · · ?? }。从上下文中可以清楚地了解用法。

为了说明，请考虑以下策略。

示例 1（固定策略）——“始终在价格区间 [$30, $50] 内提供流动性。”

示例 2（均匀 ?-reset 策略）——“在以当前价格 ?? 为中心的一系列bin区间上均匀分配流动性。当价格超出此范围时进行重置。”

示例 3（比例 ?-reset 策略1）——“让 ? = 0.5，所以 ?? 包含下一个价格分布概率质量的中间 50%。根据 ?? 中每个 bin 区间的概率按比例分配流动性。根据??进行重置。”

示例 4 （比例?-reset 策略2）——“让? = 0.5，所以 ?? 包含下一个价格分布概率质量的中间 50%。根据下一价格分布的概率质量的中间 90% 中每个bin区间的概率，按比例分配流动性。根据??进行重置。”

均匀的?-reset 策略如图 2 所示。

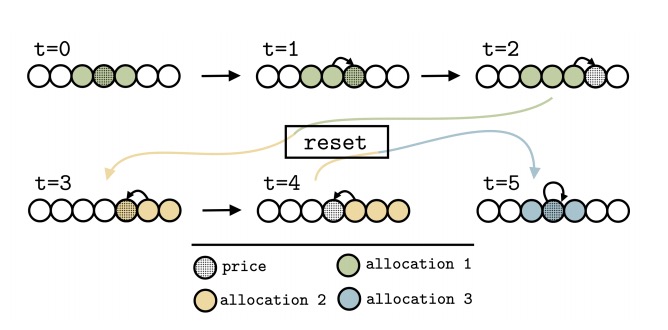
图2:均匀的?-reset策略，这里定义了三个以当前价格为中心的连续 bin区间。每个圆圈代表一个价格区间，暗色圆圈表示每个时间step的当前价格。一旦价格离开这三个连续的bin区间，策略会“重置”并在重置时将流动性重新分配到当前价格附近。

三、马尔科夫模型分析

略，有兴趣的读者可以看原文。https://arxiv.org/pdf/2106.12033.pdf

四、流动性提供策略

我们现在提出三个 ?-reset 重置策略。

4、1 比例分配策略

在这个策略中，流动性提供者（LP）根据到达某个 ? bin区间的概率按比例分配流动性。

定义 4.1。这个比例策略是带有以下条件的一种?-reset 重置策略：

（1）重置策略时的价格bin区间为?? ；

（2）最小的一组连续bin区间?? ，以 ?? 为中心，至少占下一个价格分布概率质量的 ? ；

（3）以 ?? 为中心的最小连续 bin 区间集合??，它至少占下一个价格分布的概率质量的 ? ；

（4）分配函数

?(?) ∝ ℎ(?), for ? ∈ ??, (14)

图 3 显示了比例分配策略的一个示例（在 ? > ? 的情况下）。如果 ? < ?，则? bin区间的集合将大于

? bin的区间集合。

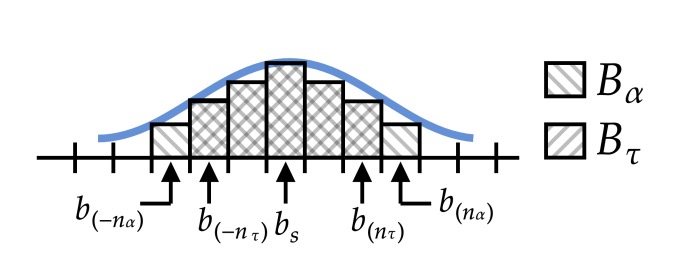
图 3：比例 ? 重置策略的示例，其中 ? > ?。条形的高度表示每个bin区间中的流动性数量。当策略最后一次重置时，价格为 ?? ，下一个价格概率分布以蓝色显示。图示了“alpha”和“tau”bin区间，在这种情况下，中间的五个 bin区间 是 ?? 和 ?? 的一部分。

4、2 均匀分配策略

在这个策略中，流动性提供者（LP）在一组? bin区间上均匀地分配流动性。

定义 4.2。均匀分配策略是一种具有以下条件的?-reset重置策略：

（1）重置策略时的价格bin区间为??。

（2）一组连续的 bin区间，?? ⊂ ?；

（3）一组连续的 bin区间，?? ⊂ ?；

（4）分配函数

?(?) = 1/(2?? + 1), for ? ∈ ??, （15）

其中 ?? 是 ?? 中的 bin区间数量。

4、3 最优流动性策略

在这个策略中，流动性提供者（LP）针对一组指定的连续bin区间??在一组? bin区间上最优地分配流动性（在?-reset重置策略中）。

定义 4.3。 最优流动性策略定义为：

(1) 重置策略时的价格bin区间为??；

（2）一组连续的 bin区间，?? ⊂ ?；

（3）一组连续的 bin区间，?? ⊂ ?；

（4）分配函数?，这是流动性优化问题的解，定义为

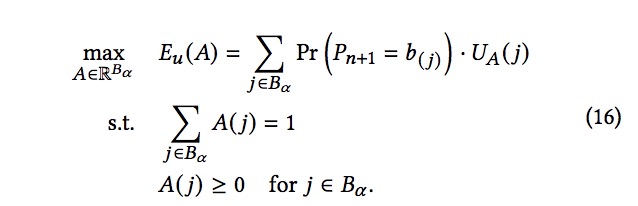
约束指定 (i) 所有流动性都已分配，并且 (ii) 分配给每个bin区间的流动性是非负的。

如果存在一个内部解，则该优化问题可通过拉格朗日乘子法（Lagrange Multiplier）得到标准解。然后用下面这个公式来表征该方案：

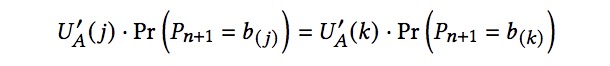
对于所有 ?, ? ∈ ?? ，以及约束

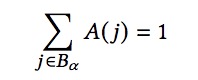
以及

?(?) ≥ 0 for ? ∈ ?? .

在实践中，我们使用SLSQP方法 [9] 来解决这个约束优化问题。

五、根据历史价格衡量策略表现

为了研究上面描述的流动性提供策略，我们使用了ETH在2018年3月-2020年4月份的价格数据（一共10万次观察数据），并以此模拟不同流动性配置策略的回报。

图4 比较了针对不同风险偏好的最优、比例以及均匀的?-reset重置策略的表现。在每种情况下，我们将 ?? 定义为最小值，使得 ?? 包含至少 50% 的下一价格分布的概率质量。

在风险中性（? = 0）和低风险情况（例如，? = 0.1）下，比例分配策略几乎是最佳的，分别为 ? = 0.14 和 ? = 0.74。在高风险情况（例如，? = 10）下，均匀分配策略接近最优，而对于极度厌恶风险的流动性提供者（例如，? = 15）而言，最优的方案就是完全均匀分配。

对于风险中立的代理人(? = 0），他们更喜欢较小的?，因为他们愿意更频繁地更新他们的配置。而对于风险规避程度更高的流动性提供者（例如，? = 3），他们更喜欢更大的 ?和由此产生的更多 bin区间来分散他们的流动性，以减少他们收到的奖励的差异。

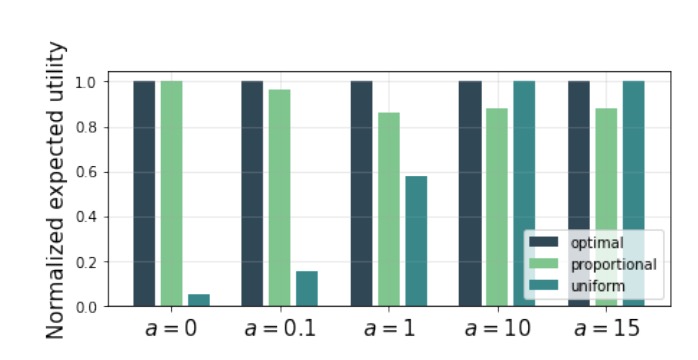
图4：不同风险偏好(?值)的最优、最佳比例及均匀分配策略的预期效用。在风险厌恶程度较低的情况下（例如，? = 0, 0.1以及1），比例分配策略的表现明显优于均匀分配。而在较高的风险规避水平下（例如 ? = 10或15），均匀分配是最优的策略。

5、1 与Uniswap v2的对比

此外，我们还可以通过历史价格数据，将以上的Uniswap v3流动性分配策略与Uniswap v2进行一个对比。

回想一下，在 Uniswap v2 中，流动性提供者（LP）是无法指定他们想要提供的流动性价格区间。

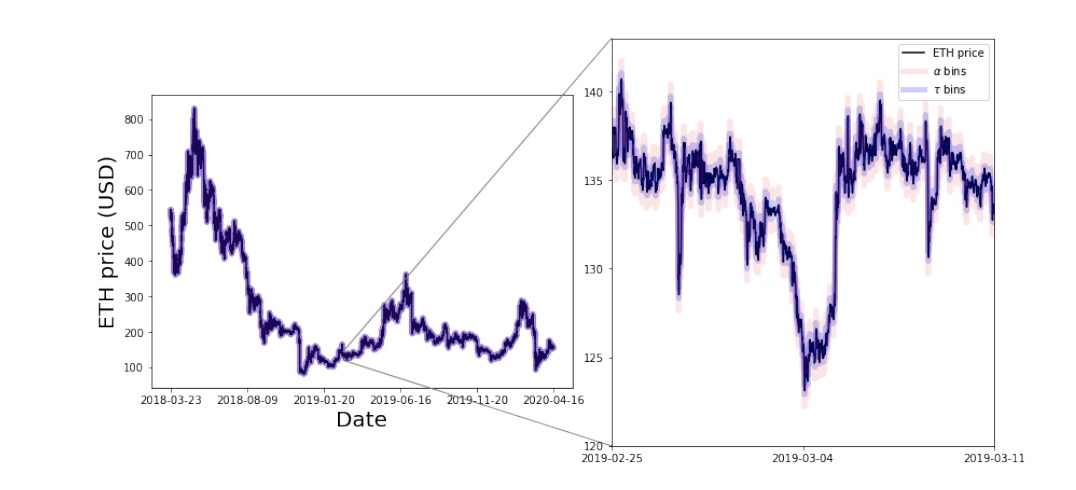
图5：使用历史以太坊价格数据回测 ? = 0.5 的最佳 ?-reset重置策略。红线表示每个时间步的 ? bin 区间的宽度，蓝线表示 ? bin 区间的宽度。与在价格区间范围内均匀提供流动性（Uniswap v2 分配）相比，通过这种最优分配策略，LP获得的效用平均提高 230 倍。

对于能规避风险的流动性提供者（? = 0.1）而言，最优?−reset重置流动性提供策略要比Uniswap v2 策略的效用高 230倍。

六、结论

本文探讨了 Uniswap v3 协议带来的流动性供应策略问题。我们提出了?-reset重置策略，并概述了一种用于分析计算它们的预期效用的技术。我们描述了该策略的三种不同实现，并比较了它们在历史ETH数据下的表现。给出? bin区间以及下一价格分布，我们能够找到最优的 ? 重置策略，通过在历史价格数据上回测我们的策略，我们发现最优?-reset策略的预期效用是Uniswap v2策略效用的 200 倍以上。

我们希望这项工作可以成为形式化和比较这些策略表现的第一步。这里提到的框架仅代表完整策略空间的一个子集，更丰富的策略类别也将根据最近的价格变动趋势修改流动性分配以及重置策略。

在多流动性提供者（LP）背景下研究流动性提供问题将是有趣的，在 Uniswap v3 上进行的策略实证研究也会很有趣。

此外，Uniswap v3 和 gas价格之间存在着有趣的宏观层面的联系。如果gas费用低，则流动性提供者（LP）就会更频繁地更新他们的头寸，而这可能会导致gas价格的上涨。了解 Uniswap与gas价格之间的动态和关系是另一个有希望的研究方向。

参考文献

[1] Hayden Adams. 2018. Uniswap Whitepaper. https://hackmd.io/@HaydenAdams/

HJ9jLsfTz

[2] Hayden Adams, Noah Zinsmeister, and Dan Robinson. 2020. Uniswap v2 core.

URl: https://uniswap.org/whitepaper. pdf (2020).

[3] Hayden Adams, Noah Zinsmeister, Moody Salem, River Keefer, and Dan Robinson.

2021. Uniswap v3 Core. (2021).

[4] Guillermo Angeris and Tarun Chitra. 2020. Improved price oracles: Constant

function market makers. In Proceedings of the 2nd ACM Conference on Advances

in Financial Technologies. 80–91.

[5] Guillermo Angeris, Alex Evans, and Tarun Chitra. 2020. When does the tail wag

the dog? Curvature and market making. arXiv preprint arXiv:2012.08040 (2020).

[6] Guillermo Angeris, Hsien-Tang Kao, Rei Chiang, Charlie Noyes, and Tarun Chitra.

2019. An analysis of Uniswap markets. arXiv preprint arXiv:1911.03380 (2019).

[7] Jun Aoyagi. 2020. Lazy liquidity in automated market making. Available at SSRN

3674178 (2020).

[8] Kenneth Joseph Arrow. 1965. Aspects of the theory of risk-bearing. Helsinki.

[9] Paul T Boggs and Jon W Tolle. 1995. Sequential quadratic programming. Acta

numerica 4 (1995), 1–51.

[10] Alex Evans. 2020. Liquidity provider returns in geometric mean markets. arXiv

preprint arXiv:2006.08806 (2020).

[11] Alex Evans, Guillermo Angeris, and Tarun Chitra. 2021. Optimal Fees for Geometric Mean Market Makers. (2021).

[12] Bhaskar Krishnamachari, Qi Feng, and Eugenio Grippo. 2021. Dynamic Curves

for Decentralized Autonomous Cryptocurrency Exchanges. arXiv preprint

arXiv:2101.02778 (2021).

[13] Max. 2021. Introducing Alpha Vaults — an LP strategy for Uniswap

V3. https://medium.com/charmfinance/introducing-alpha-vaults-an-lpstrategy-for-uniswap-v3-ebf500b67796

[14] John W Pratt. 1978. Risk aversion in the small and in the large. In Uncertainty in

economics. Elsevier, 59–79.

[15] DeFi Pulse. 2021. Defi Pulse. https://defipulse.com/

[16] Martin Tassy and David White. 2020. Growth rate of a liquidity provider’s wealth

in xy= c automated market makers.

[17] Uniswap team. 2021. Uniswap v3 Analytics. https://info.uniswap.org/#/

[18] Dave White, Martin Tassy, Charlie Noyes, and Dan Robinson. 2020. Uniswap’s

Financial Alchemy. https://research.paradigm.xyz/uniswaps-alchemy