超越白皮书：DEX稳定币挖矿真的无损么？

本报告由火币区块链研究院出品，报告发布时间2020年12月4日 ，作者：胥彤，赵文琦，袁煜明

摘 要：

DEX是Defi最重要的基础设施，其中Curve一直以“稳定币版的Uniswap”为人所知，并以其低滑点的特征成为交易稳定币的首选平台，吸引了大量流动性提供者进行质押挖矿，但流动性提供者往往会发现收益不及预期。

基于此，本文首先分析了Curve运作的核心机制——StableSwap模型，其对恒定求和公式和恒定乘积公式做了融合，形成一条介于恒定求和以及恒定乘积之间的曲线，使得用户在一定区域交易时价格相对稳定，避免滑点问题，也大大降低了流动性提供者（LP）的无常损失风险，因此给用户留下了“低磨损”的印象。

但我们通过查看代码，发现在用户在Curve中进行充币、提币等操作时都有潜在损失的可能，这也是用户收益不及预期的重要原因。因此，本文第二章基于前述Curve的做市机制，讨论了在Curve中作为流动性提供者的损失来源及规避措施，为LP操作提供了参考。具体来说损失主要会在三个场景产生，(1)不同于Uniswap上LP必须按照当时流动池中两个币种的比例来提供流动性，Curve允许LP进行单边充提，但用户在充币时可能产生铸币凭证比例损失和惩罚费用，(2)如果将流动池充到失衡状态还会为套利者提供机会，(3)而在提币时如果让流动池偏离平衡状态，会提走少于销毁的凭证比例的代币，同时也面临惩罚费用的损失，损失的大小与当时流动池的状态和充提造成的失衡程度有关，当然如果在充提过程将流动池推回平衡状态，也会获得一定的奖励。

基于以上讨论，我们建议LP无论充币还是提币，都尽量让流动池回归到平衡状态。如果充提数量不多影响不大，但如果资金量较大，建议LP先做好测算权衡一下损失，或者是将资金分批充入或提出，待流动池恢复稳定之后继续操作。

一、白皮书都说了什么

1.1 背景

Dex是今年Defi浪潮中崛起的最重要的基础设施，对于普通用户而言，除了去中心化钱包，最熟悉的去中心化产品应当就是Dex。2019年整年，Dex的交易量不过30亿，但在今年，9月和10月的交易量分别是这个数字的约9倍和7倍。而这其中，近三个月长期占据交易量前三的Uniswap、Sushiswap、Curve均是自动做市类型的Dex。

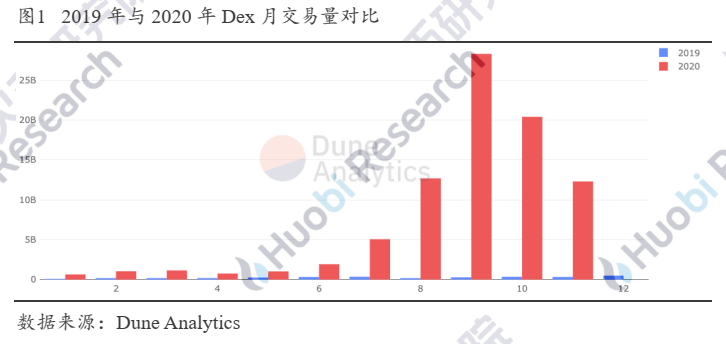
Curve一直以“稳定币版的Uniswap”为人所知，并以其低滑点的特征成为交易稳定币的首选平台。其流动性池的余额峰值一度超过16亿美金，月交易量也长期维持在10亿美金以上。在聚合交易平台1inch上，Curve的月交易占比峰值达26.84%，周交易占比峰值达45.5%。

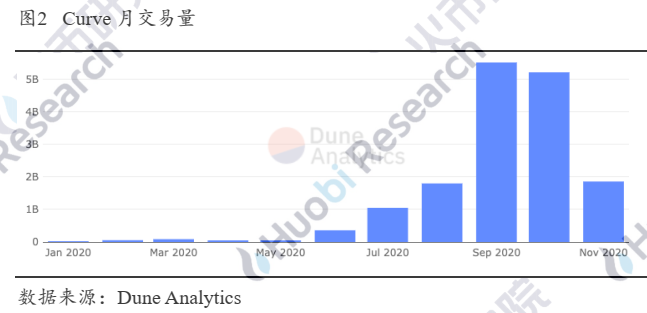
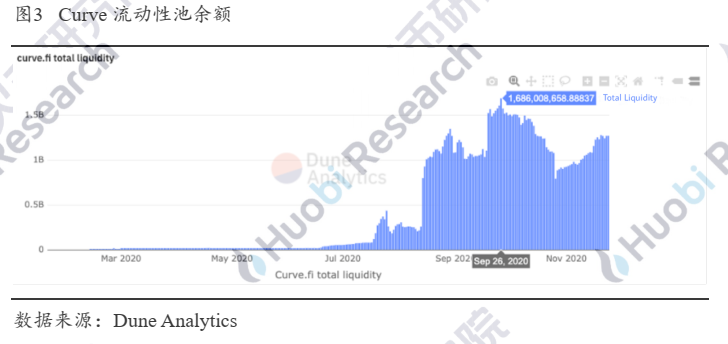
值得注意的是，对比Uniswap理论上无上限的交易对数目，Curve迄今也只有19个交易池。如此少的交易池却能吸引如此多的资产沉淀和交易量，究其原因，是因为其做市模型给交易者带来了“低滑点”的印象，同时给流动性提供者带来了“低磨损”的印象，使得苦无偿损失和滑点久矣的大资金涌入其中。但事实真和大家的印象一致么？

为了回答这个问题，本文的第一章将和读者一起翻开Curve的白皮书，介绍Curve运作的核心机制；第二章将基于这个机制讲解在Curve中作为流动性提供者的损失来源；第三章对损失进行了总结并阐述如何规避这些损失。希望通过本文能揭示那些“莫名其妙”损失的资金到底去哪里了，并分析如何合理规避损失。

1.2 的做市机制简述

Curve的做市机制最核心的思想在于， 在降低交易滑点的同时保证池子在任何价位下都能提供流动性 。为了实现这个目的，Curve在白皮书中提出了StableSwap[1]模型，其结合了恒定求和以及恒定乘积的做市方式。为方便理解，虽然StableSwap支持多元做市，但本章在讲述过程中主要使用二元做市模型，但其原理是相通的。

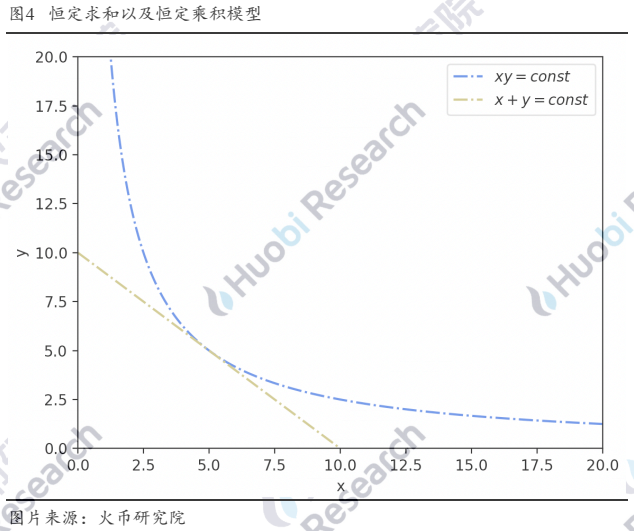
恒定求和类的做市公式，如x+y=const因为曲线的斜率恒定，能够实现零滑点的交易，用户用一定量的x总是可以换出等量的y，注入资产与换出资产的比率不会随着注入量的变动而变动。但是这类做市模型会遭遇流动性枯竭的问题，x或 y都可能被以低代价清空，如图4中的x+y=10曲线，只需要至多10个x就可以清空y。

恒定乘积类的做市公式，如xy=const，则没有流动性枯竭的问题，其曲线沿着坐标轴无限延伸，这意味着用户在注入资产后总是可以换得另一种资产。但该种模式会带来滑点问题，任何x与y的兑换都会导致点(x,y)沿着曲线移动，且曲线的斜率一直在变动，意味着价格一直在变动，导致用户不可能以当前时刻的价格完成所有的兑换，带来滑点。此外，对于流动性提供者来说，在该种做市模型下，会面临遭受无常损失的风险，因为价格是沿着曲线连续变动的，导致流动性提供者需要承担变动过程中的非最优成交价格。

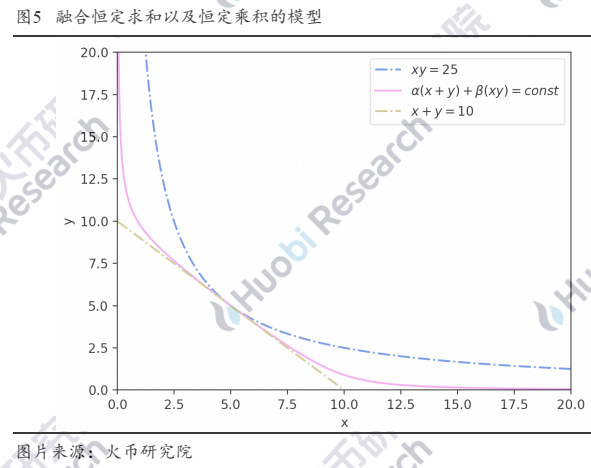
Curve的StableSwap融合了两者，为了便于理解，可以先简单将其视为对恒定求和以及恒定乘积做了加权求和，形成α(x+y)+β(xy)=const的形式。如图5所示，形成一条介于恒定求和以及恒定乘积之间的曲线，类似“平底锅”的二维投影。

用户在“平底”区域交易的时候，价格相对稳定，避免滑点问题 。但价格的稳定也意味着该种做市模型 不适合相对价格波动较大的资产 ，我们也能注意到Curve的同一个池子中都是价格相对稳定的资产，如各类稳定币池和锚定BTC的池子。对于流动性提供者来说，该种模型也 大大降低了无常损失的风险 ，只要价格不震出“平底”区域，无偿损失相对于恒定乘积做市会小很多，即便价格被震到“锅边”，也会快速被套利者套回到“平底”区域。

同时“锅边”无限延伸，避免流动性枯竭的问题 。在任何价格上，任何一个资产都不会被清空，但可能滑点会非常高。

1.3 进一步理解Curve做市模型

上一小节简要介绍了Curve的做市机制，为了便于读者理解后续章节的内容，本小节将进一步从数理角度介绍Curve的做市模型。

首先，从普遍的角度来说，对于恒定求和的做市机制，其做市依据如下不变式，即池子中各个代币数量之和为常数：

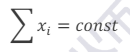
对于恒定乘积的做市机制，其做市依据如下不变式，池子中各个代币按权重求做幂运算后求乘积为常数：

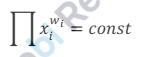
实际运用在Curve中的不变式稍微做了简化，其最底层的两个不变式为：

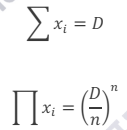
其中D代表池子中每种代币的价格(或数量)都相等时，池子中代币的总数量。

在上述两个式子的基础上，StableSwap引入了χ作为恒定求和的权重，在χ=0时，不变式变为恒定乘积；在χ→∞时，不变式为恒定求和；当χ属于中间某个值时，就是StableSwap期待的对恒定乘积和核定求和两个不变式的综合。另外，为了在恒定求和中也体现出代币总数的影响，StableSwap对恒定求和不变式两边同时乘以了χD^(n-1)后再与恒定乘积不变式加和，得到其做市的不变式：

χD^(n-1) ∑▒x_i +∏▒x_i =χD^n+(D/n)^n

在此基础上，为了让χ可以调节以适应理想价格偏离相对价格为1的情况，StableSwap引入了常数A和变量(∏▒x_i )/(D⁄n)^n ，令

χ=(A∏▒x_i )/(D⁄n)^n

从上式中可以看出，χ可以看作是A和(∏▒x_i )/(D⁄n)^n 的乘积。(∏▒x_i )/(D⁄n)^n 可以理解为池子的对称性，当池子中每种代币的分布完全均衡的时候，(∏▒x_i )/(D⁄n)^n =1，χ=A；而当池子代币分布极度不均匀时，(∏▒x_i )/(D⁄n)^n 趋近于零，χ趋近于零，做市公式退化为恒定乘积做市公式。因为恒定求和的做市公式适用于相对价格没有波动且为1的场景，当池子的代币数量分配极不均衡时意味着相对价格大幅偏离于1，此时恒定求和公式是不适用的。将χ代入做市公式可以得到最终的用于做市的不变式如下：

An^n ∑▒x_i +D= ADn^n+D^(n+1)/(n^n ∏▒x_i )

根据上述公式做市时，代币的交易会影响x_i的值，以3pool的(DAI, USDC, USDT)为例，假设交易前其数量分别为(x_1,x_2,x_3 )，当充入x_1^'-x_1个DAI换取USDT时，x_1的值会变为x_1^'，将x_1^'代入上式计算出新的x_3^'，x_3^'-x_3即为换取到的USDT的个数，在这个过程中A和D均不会发生变化。从图形上看，交易会使池子的状态沿着图5中的粉色曲线移动(为了方便可视化，本章节中均以双变量场景作图)。

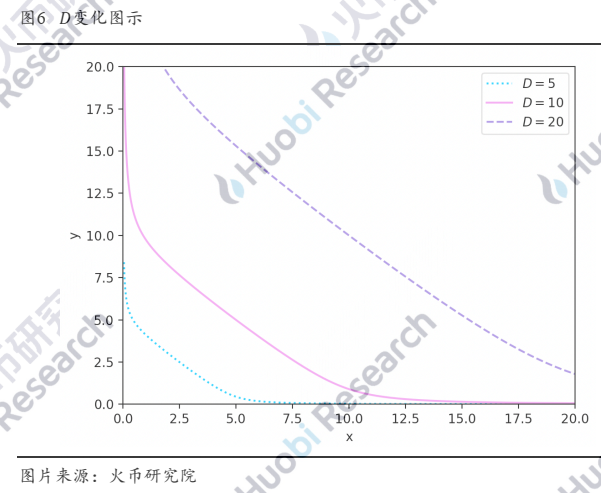
但A和D并不会一直保持不变。对于D来说，当流动性提供者向池子中充入或提出流动性时，D会相应变化。依据前述做市不变式，充提动作发生时，会根据新的x_i值重新计算当前状态下的D值。充入时D会变大，取出时D会变小。如图6所示，在A不变的情况下，可以看出D增大会使曲线向外推移，同时“平底”区域也会放大，反之亦然。

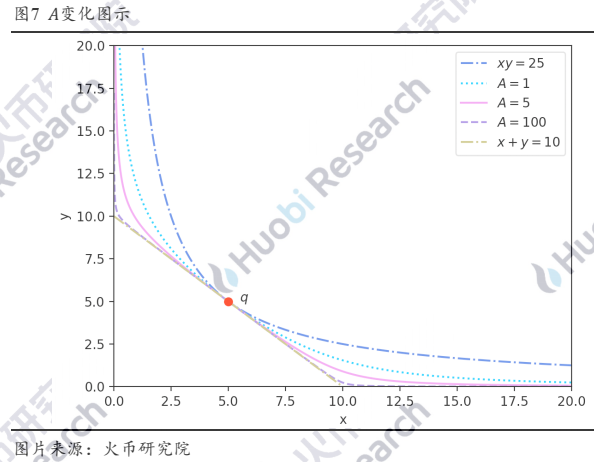
A是一个可以调整的参数，在Curve中可以通过提案和投票的形式对各个池子的A进行修改 。在D不变的情况下，从图7中可以清晰的看出A的变化对做市曲线带来的影响。A越大，曲线越接近恒定求和做市曲线，“平底”区域越大，反之越靠近恒定求和曲线，“平底”区域越小。

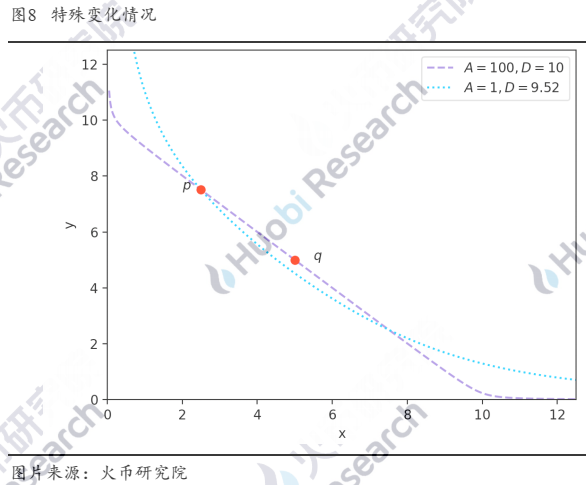
图7中，虽然A的变化会带来曲率的变化，但是这些曲线都会经过点q，也就是他们和x=y的交点，因为这个时候D没有发生变化。但是在特殊情况下，A的变化会联动D的变化。如图8所示，假设原本的做市曲线在A=100,D=10这条曲线上，池子中代币的数量在q(5,5)点，这时有一笔交易发生，将池子中的代币数量转移到了p(2.50,7.51)点。若此时社区投票主动将A从100变更为1，池子的代币数量不变（没有新交易发生，也没有充提行为），为了使做市恒等式仍然成立，D会被动发生改变，新的曲线仍将经过点p，最终将曲线推至A=1,D=9.52。这是A和D同时变动的情况。在这个变换的过程中，攻击者可以通过价差套利[2]，不过目前在Curve中这个可套利的漏洞已经被修复[3]。

总而言之，通过对Curve机制的深入理解可以看出其在设计上确实是为了实现低滑点，并且因其支持的交易对相对价格稳定因此也一定程度上减少了无常损失。因此Curve留给用户非常强的“低交易磨损、低做市磨损”的印象。但如果用户基于这个印象无顾忌地在Curve中进行操作，则有可能面临意想不到的损失。在下一章中我们将详细分析损失的来源。

二、损失来源

Curve做市与Uniswap不同，在Uniswap上LP必须按照当时流动池中两个币种的比例来提供流动性，而Curve允许LP不按照比例充值，甚至可以单边充值。在火币研究院之前的研究《AMM做市无常损失对冲分析系列（一）——损益模型构建》中，我们已经讨论过，在AMM机制下，池子中币种比例失衡会给LP带来损失，其中主要是无常损失，那对于Curve的LP来说，这种流动性供应机制是否会带来除无常损失以外的其他损失呢？我们通过查看Curve 3Pool的代码，发现了很多白皮书上没有提及的细节，在充币、提币，包括引起池子中币种失衡而给套利者提供机会等环节都有潜在损失的可能，这也是造成LP挖矿收益不及预期的原因。

以下将按照整个LP供应环节的流程来分析中间可能产生的损失。为方便说明，本章论述以二元做市为例，将3Pool简化为2Pool。

2.1 充币

a. 铸造凭证损失——单边充币

我们知道，LP将代币充进流动池后，平台会铸造一定数量的凭证返回给LP，交易手续费的分红，治理代币的分配，以及最后的提币都由该凭证占流动池中总凭证的比例来决定。那铸造出的凭证数量如何确定呢？我们前面提到Curve做市公式里的D值，假设此前2Pool的D值为D_0，平台已发的总凭证数量为Total Supply, 充入代币后D值变为D_1，则新的流动性提供者获得的凭证数量为：

Token Supply=Total Supply×(D_1-D_0)/D_0

由Curve做市公式的性质，当有新的代币充入后，D值会对应放大，但不是根据充入的数量等比放大，假设流动池中代币总量一定，只有两种代币数量相等时D值最大，相差数量越多D值越小，LP就会获得与提供代币价值不成比例的凭证。下面我们来做图说明。

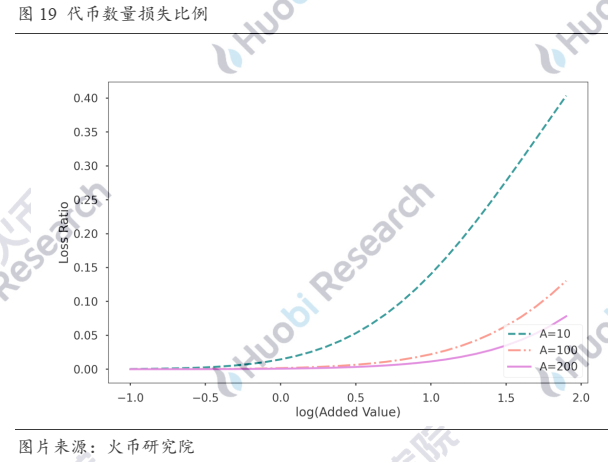
假设2Pool中有两种代币，USDC和USDT，两者的合理价格比为1:1，流动池初始处于完美平衡状态，两种代币数量均为10,000,000，初始流动性池数量为N_0。LP选择单边充币，则冲入的数量与凭证数量损失比例的关系如下图：

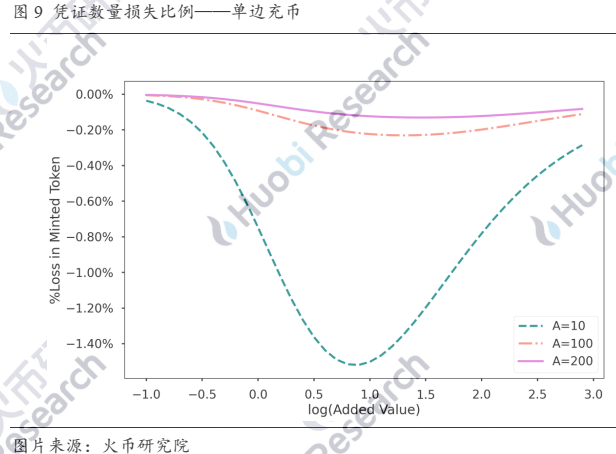
图中横坐标x表示冲入的代币数量相对初始代币数量的log值，即充币数量为N_0×〖10〗^x，纵坐标表示LP充入代币数量与总体代币数量的比值与新铸造出的凭证占总体凭证比例的差值。可以看到，如果流动池此前已是平衡状态，单边充币会造成凭证数量的损失，且随着充币数量的增加，凭证数量损失在到达极值之后会逐渐缩小，因为在池中占比够大而逐渐收复了“话语权”。另外，A值变大可以平滑掉一部分的损失，使得到达极值的区间放大。

图10是以充币的绝对数量展示的凭证损失，依然是假设在充币前流动池中两个稳定币的数量均为10,000,000，也符合当前大部分流动池质押的数量级。在充币资金量较少的时候，损失变化比较迅速，我们放大一下资金量较低的部分，如图11所示，可以更清楚地看到在资金体量较小时损失的变化情况。

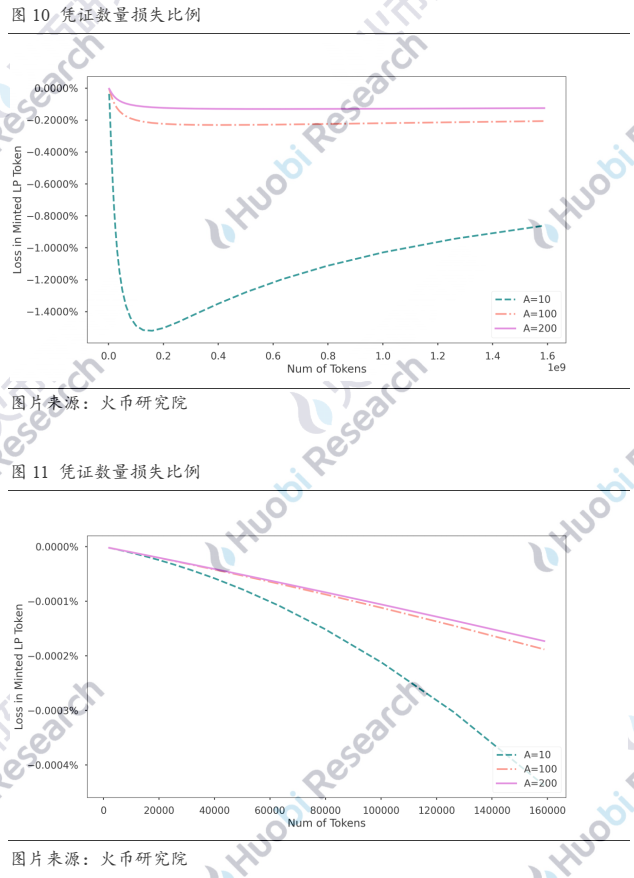
我们从另一个角度来看——偏度，Curve项目方提出了偏度的概念，用来衡量流动池中各代币的平衡程度，计算方法如下：

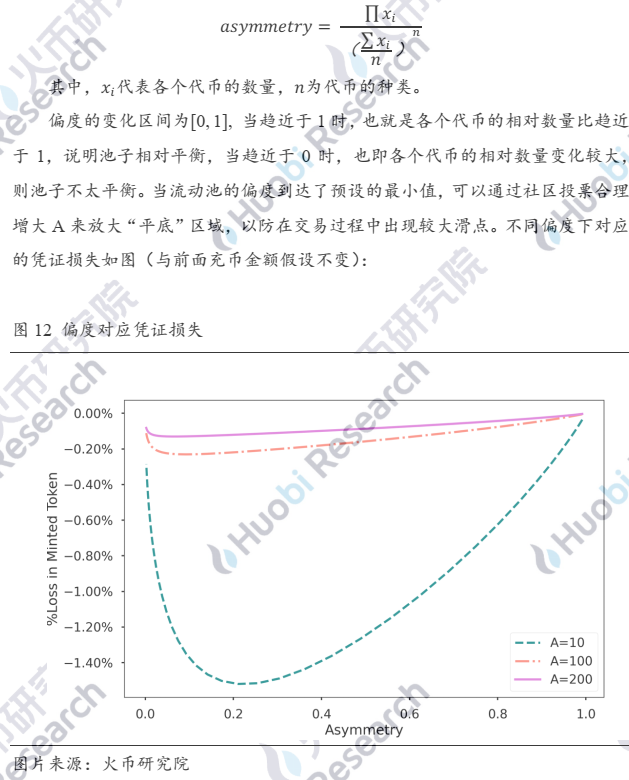
只要是偏离完美平衡状态，新铸的凭证总是会有一定比例的损失。

b. 铸造凭证损失——双边充币

那如果进行双币充值呢？同样假设流动池之前处于平衡状态，新注入的双币数量与此前池中数量总数一样，但比例不同。

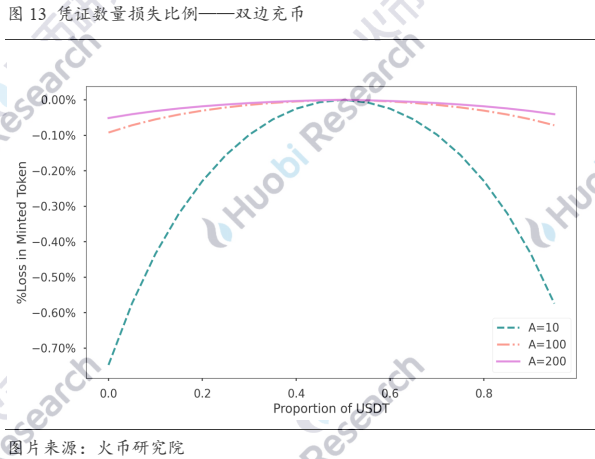
图中横坐标为其中一个币种（假设为USDT）所占充币数量的比例，可以看出，只要是偏离了1:1的平衡状态，都会带来新铸凭证数量的损失，且偏离度越大，损失越大。

那如果流动池此前就已不是平衡状态呢？同样假设新注入的双币数量与此前池中数量总数一样，但池中此前USDT与USDC的数量比不同，下图展示了不同比例情况下铸造凭证数量的损失。

图14 充币比例对应凭证数量损失

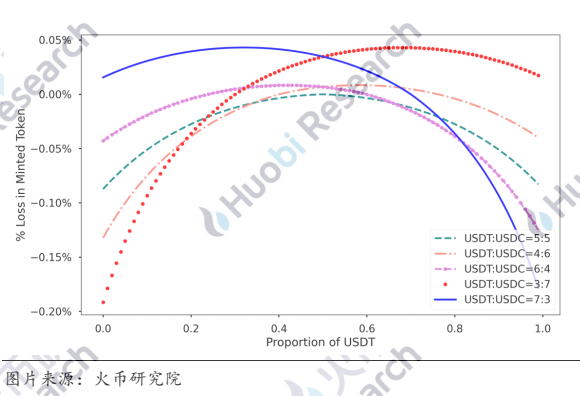
相比于两者此前数量为1:1时只要不按照比例充币都会造成损失的情况，当提供份额较低的代币，在一定范围内，不仅没有损失，还可以获得存款奖励，如果将流动池补齐为1:1的状态，获得的奖励最多，这与前面论述的D值的性质一致，即总量一定，两币种数量越接近，D值越大。

考虑这样一种场景，此前流动池是1:1状态，第一个流动性提供者LP1不按最优比例充币之后，新的流动性提供者LP2又将流动池补齐，则前一个LP1获得的凭证比例会面临两次打折，首先是因为将流动池充离平衡态获得了低于提供资金量比例的凭证，之后因为LP2将流动池拉回平衡态而获得了一定的奖励，使得LP1凭证占比更低。

c. 惩罚费用

我们在查看Curve代码时注意到，在LP提供流动性时，如果不按照理想值充币，平台会扣除一笔管理费，那理想值是如何定义的呢？

假设此前2Pool的双币数量为[x_1,x_2 ]，D值为D_0，LP新提供的双币数量为[x_1^',x_2^' ]，在池中双币数量为[x_1+x_1^',x_2+ x_2^' ]时对应的D值为D_1，则流动池默认的双币理想数量为[x_1×D_1/D_0 ,x_2×D_1/D_0 ]，会对差值部分的绝对值，即[|x_1×(D_1-D_0)/D_0 -x_1^' |,|x_2×(D_1-D_0)/D_0 - x_2^' |]按费率扣除一定数量的代币。仍然假设新充入的双币数量与此前池中总数量一样，为20,000,000个，则在此前USDT：USDC分别为4:6，5:5，6:4的情况下，对应不同充币比例，充币之后平台扣除的代币数量如下图：

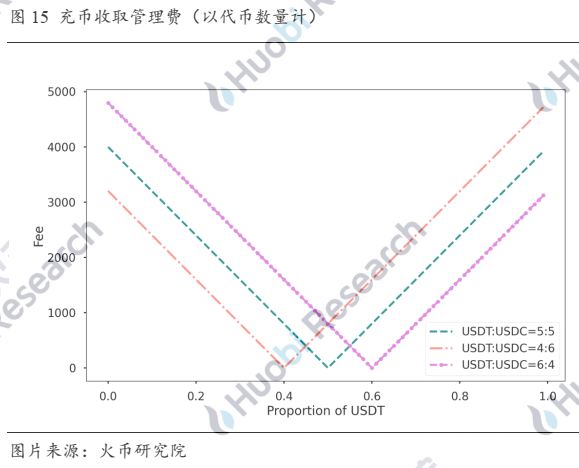
与此前铸造凭证时鼓励将流动池推至平衡状态不同，当新充币的比例与初始比例不同时就会产生费用，从费用角度考虑，流动池默认的最优状态是将池中代币数量等比放大，此时收取的费用最少，为0。

我们将铸造凭证数量损失和费用损失放在一起来看，这里的假设是LP提供的代币总量与流动池此前代币总量相同，整体的充币损失如下面两张图所示。

图16 充币损失（流动池之前处于平衡状态）

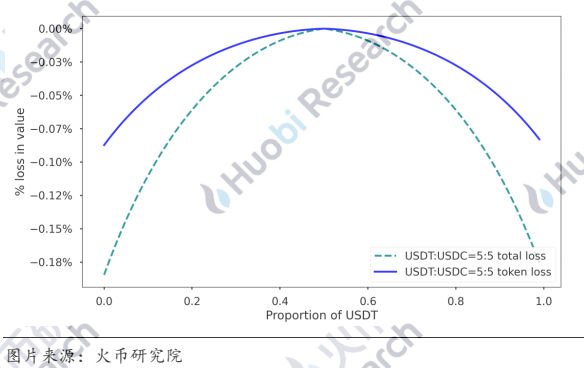
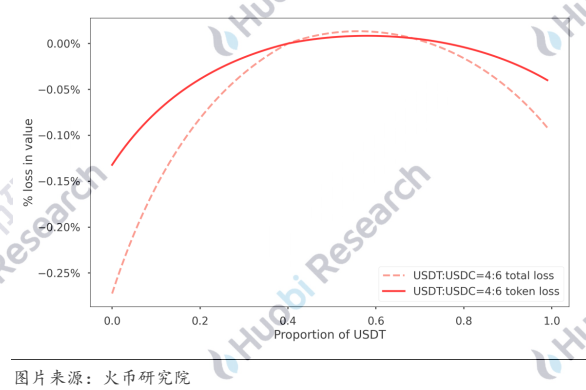
这里的纵坐标表示，LP提供流动性之后获得的凭证对应的流动池代币数量相比于提供的代币数量之间的损失，在流动池平衡与不平衡两种状态下，结果有些许差异。平衡时，只要充币不是按照1:1，就会造成损失，而如果此前流动池不平衡，如图13所示在USDT：USDC=4:6的条件下，费用的最小点在4:6的位置而铸造凭证损失的最小点在6:4的位置，综合起来，整体损失最小的位置在[0.5, 0.6]之间，且在一定范围内，整体效果并没有损失，具体位置与资金体量也有关系，这里不再进行详细的计算。

2.2 套利

我们在第一部分讨论过，Curve通过调整A参数来改变“平底”区域的范围，在该区域内，交易的滑点非常低，使得稳定币之间的兑换在合理价格内，但从图5也可以看到，一旦充币致使偏离该区域到了拐点以外，滑点甚至比Uniswap的做市公式还大，就会给套利者提供非常大的空间。如果此前流动池中币的数量较少，新的LP提供者又单边充入了大量的资金，即便是在A值较大的情况下，也可能突破拐点，使得代币在Curve上的价格与在其他交易所出现较大差异，从而给套利者提供机会。下图展示了在不同A值条件下单边充币，套利者将流动池套回平衡状态后对应的套利平均价格。

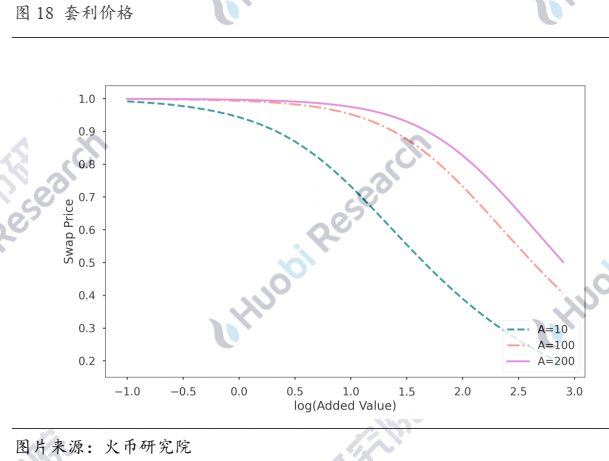
在交易过程中，D值是不变的，由Curve做市公式的性质，D不变时，两种代币数量越接近，代币总量越小，于是套利者完成套利后，用较小的资金量换走了池中份额较高的代币，总体代币数量降低，那相应的LP都会面临代币减少的损失，在不同资金体量下发生套利后，池中减少的代币数量比例如下图所示。

在真实的场景中，套利者不会套回到最均衡的位置，在已发生的案例中，我们看到有的套利者是采用闪电贷进行无风险套利，利用事先写好的套利机器人不断监控市场价格发现套利机会，当扫描到有漏洞的交易时，在无需任何抵押的情况下进行贷款，借贷、套利、还款都在一个区块中完成。考虑到借贷成本，以及池中两个稳定币价格的微小差异，均衡点不是做市曲线滑点最低的位置。

2.3 提币

a. 不平衡状态单边取出

假设流动池初始处于不平衡状态，LP将致使流动池偏离平衡状态的代币取出。

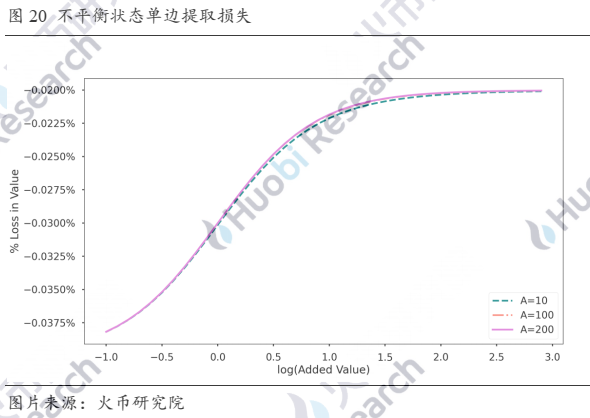
图中横坐标x表示提币的代币数量相对初始代币数量的log值，即提币数量为N_0×〖10〗^x，在提出之后，流动池回归完美平衡状态。纵坐标y表示相比最初时LP提供的代币，取出后损失的比例。我们可以看到，与充币过程损失先大后小不同，池子初始偏离度越高，提出后损失越小，在达到一定数量级后，损失基本维持在0.02%，只有手续费损失。这是因为在平台计算应提币的数量时，先根据做市公式确定当前的D值，然后根据提币凭证数量等比计算出新的D值。

假设在提币前2Pool的D值为D_0，平台已发的总凭证数量为Total Supply, 提币对应的凭证数量为Token Amount, 则提币后D_1的值变为

D_1=D_0×（1-(Token Amount)/(Total Supply)）

之后将D_1代入做市公式得到流动池中两种代币的数量，与初始代币数量的差值即为提出的代币数量。如果提出流动池中相对过量的币种，平台会有一定的补偿效应，如下图。

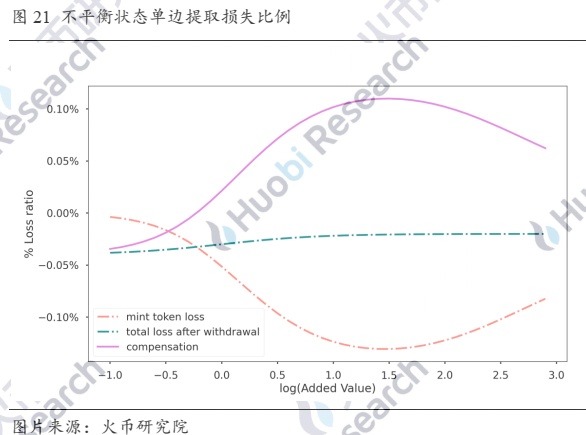
b. 平衡状态不平衡取出

如果流动池本身处于平衡状态，那单边提取会造成什么影响呢？

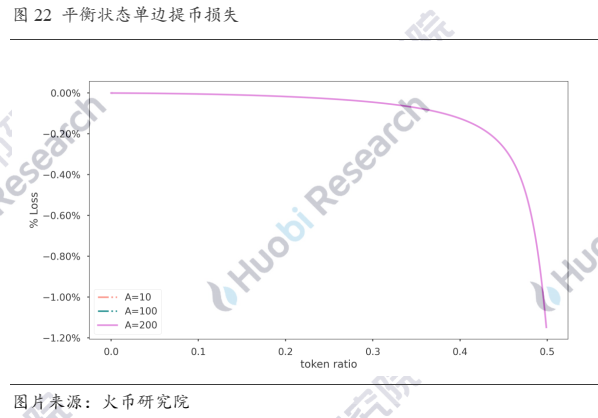
这里，横坐标x表示提币凭证与发行总凭证的比例，纵坐标y表示提出币的数量的损失，计算方法是，取出的数量与总数量的比值和提币凭证与发行总凭证的比例的差值。不同A值对此没有影响，随着单边提取比例的增加，损失会逐渐增速。

c. 惩罚费用

同样类似于充币过程，在LP提币时，如果不按照理想值提取，平台也会扣除一笔费用，计算过程与充币环节一致。

2.4 3Pool实例

我们以3Pool的真实数据来举个例子。截至撰稿，3Pool中3个稳定币DAI、USDC、USDT的数量分别为79,947,203.64 (24.58%)、134,425,652.93 (41.32%)、110,925,927.58 (34.10%)，流动池中代币的总数量为325,298,784.15，手续费率为0.04%，管理费率为0.02%，A值为200。

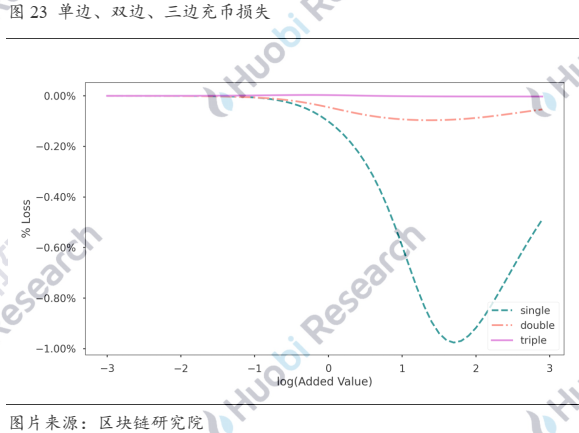
横坐标x表示冲入的代币数量相对流动池中代币总数量的log值，上图分别展示了单边、双边、三边充币造成损失的比例，这里双边充币是指充入USDT和USDC，单边充币是指充入USDT。我们注意到在池子中，DAI相对于USDT和USDC的数量是不足的，如果单边充入的币种是DAI，流动池在一定充币数量范围内对LP还有所奖励，如下图所示。

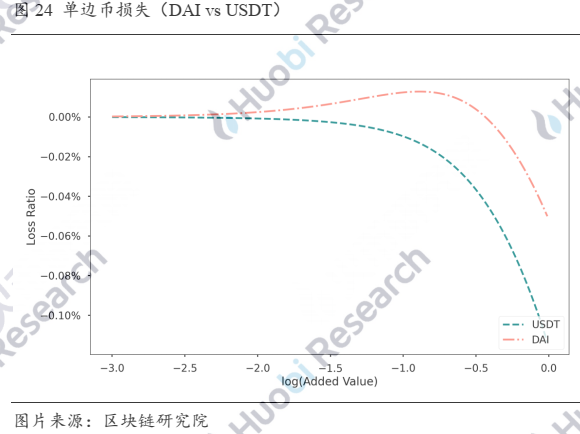
那如果是单边提币呢？下图展示了分别单边提取DAI、USDC和USDT时LP的损失，横坐标表示单边提取的数量占该币种在流动池中总数量的比例。由于DAI在池中占少数，提币时损失增大的速度快于USDT和USDC。

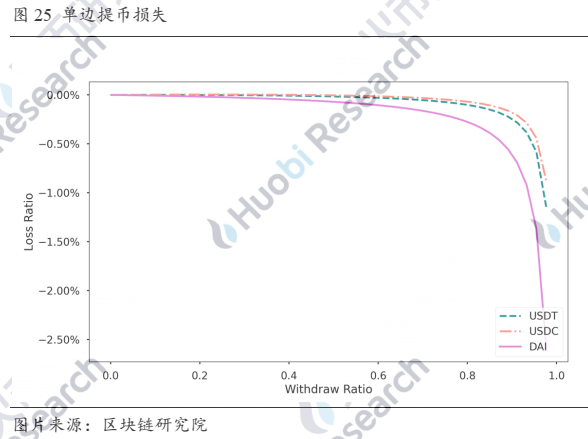
三、如何规避损失

我们前面讨论了在LP充币、流动池发生套利交易和提币环节因为池子状态和充提比例问题可能引起的潜在损失，总结如下：

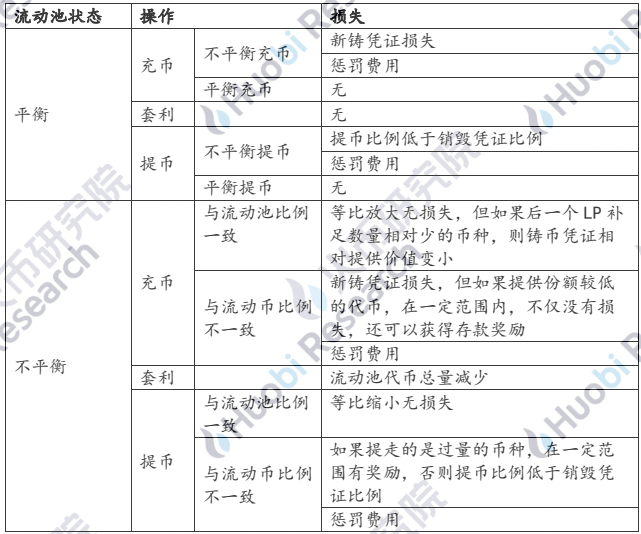
那对LP来说，如何操作比较合理呢？

最理想的状态是无论充币还是提币，都尽量让流动池回归到平衡状态，即在充币时补齐量少的币种，提币时提走量多的币种。但LP手里未必是刚好有流动池中量少的币，如果充提数量不多，那整体而言损失都不会很大，如果充提量很大，建议LP最好首先做一下测算，看是不是会将流动池推到拐点的位置，权衡一下可能的损失，或者是将资金分批充入，待流动池恢复稳定之后再充入下一笔。提币时也是类似的操作。

参考文献

[1] 白皮书：StableSwap - efficient mechanismfor Stablecoin liquidity, https://www.curve.fi/stableswap-paper.pdf

[2] Curve Vulnerability Report：https://medium.com/@peter_4205/curve-vulnerability-report-a1d7630140ec

[3] Curve提案修复潜在可套利漏洞：https://dao.curve.fi/vote/ownership/22

[4] Curve代码：https://github.com/curvefi/curve-contract/tree/master/contracts

免责声明

1.火币区块链研究院与本报告中所涉及的项目或其他第三方不存在任何影响 报告客观性、独立性、公正性的关联关系。

2.本报告所引用的资料及数据均来自合规渠道，资料及数据的出处皆被火币区块链研究院认为可靠，且已对其真实性、准确性及完整性进行了必要的核查，但火币区块链研究院不对其真实性、准确性或完整性做出任何保证。

3.报告的内容仅供参考，报告中的结论和观点不构成相关数字资产的任何投资建议。火币区块链研究院不对因使用本报告内容而导致的损失承担任何责任，除非法律法规有明确规定。读者不应仅依据本报告作出投资决策，也不应依据本报告丧失独立判断的能力。

4.本报告所载资料、意见及推测仅反映研究人员于定稿本报告当日的判断，未来基于行业变化和数据信息的更新，存在观点与判断更新的可能性。

5.本报告版权仅为火币区块链研究院所有，如需引用本报告内容，请注明出处。 如需大幅引用请事先告知，并在允许的范围内使用。在任何情况下不得对本 报告进行任何有悖原意的引用、删节和修改。