什么是椭圆曲线数字签名算法（ECDSA）？

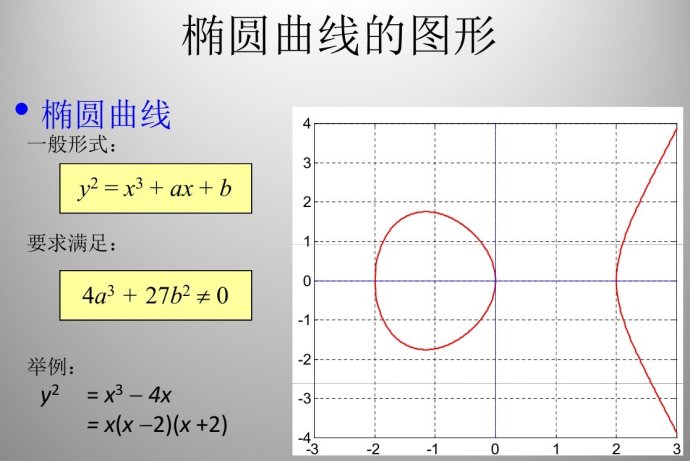
椭圆曲线数字签名算法（ECDSA）是使用 椭圆曲线密码（ECC） 对数字签名算法（DSA）的模拟。 ECDSA于1999年成为ANSI标准，并于2000年成为IEEE和NIST标准。它在1998年既已为ISO所接受，并且包含它的其他一些标准亦在ISO的考虑之中。与普通的离散对数问题（discrete logarithm problem  DLP）和大数分解问题（integer factorization problem  IFP）不同，椭圆曲线离散对数问题（elliptic curve discrete logarithm problem  ECDLP）没有亚指数时间的解决方法。 因此椭圆曲线密码的单位比特强度要高于其他公钥体制。

数字签名算法（DSA）在联邦信息处理标准FIPS中有详细论述，称为数字签名标准。它的安全性基于素域上的离散对数问题。椭圆曲线密码（ECC）由Neal Koblitz和Victor Miller于1985年发明。它可以看作是椭圆曲线对先前基于离散对数问题（DLP）的密码系统的模拟，只是群元素由素域中的元素数换为有限域上的椭圆曲线上的点。椭圆曲线密码体制的安全性基于椭圆曲线离散对数问题（ECDLP）的难解性。椭圆曲线离散对数问题远难于离散对数问题，椭圆曲线密码系统的单位比特强度要远高于传统的离散对数系统。因此在使用较短的密钥的情况下，ECC可以达到于DL系统相同的安全级别。这带来的好处就是计算参数更小，密钥更短，运算速度更快，签名也更加短小。因此椭圆曲线密码尤其适用于处理能力、存储空间、带宽及功耗受限的场合。

ECDSA是椭圆曲线对DSA的模拟。ECDSA首先由Scott和Vanstone在1992年为了响应NIST对数字签名标准（DSS）的要求而提出。ECDSA于1998年作为ISO标准被采纳，在1999年作为ANSI标准被采纳，并于2000年成为IEEE和FIPS标准。包含它的其他一些标准亦在ISO的考虑之中。