超导体（superconductor），指可以在特定温度以下，呈现电阻为零的导体。超导体电阻转变为零的温度，称为超导临界温度。 —— 前言

有别于之前推出的 MOV 磁力交易和闪兑交易，【MOV 超导】属于一种新型的自动化交易市场，有着非常强大的做市机制和流动性，可以针对不同门类的交易对进行函数定制化做市，如稳定币间、主流币间、小币种间以及合成资产间等。MOV 超导核心技术可以归类于 CFMM(Constant Function Market Maker) 【1】做市机制，即恒定函数做市商，最著名的代表项目有 Uniswap 和 Balancer，一个是恒定乘积做市函数【2】，一个是恒定加权几何平均做市函数【3】。在描述 CFMM 之前，我们有必要介绍一下 LMSR，一个“古老”的自动化做市机制，可以称之为 CFMM 鼻祖，体会金融中的数学之美。

LMSR

在现代金融市场和理论中，市场评分规则（market scoring rule）常用于计算交易者与做市商之间达成交易的成本。其中最常用的是对数市场评分规则 LMSR(Logarithm Market Scoring Rule)【4】。根据 LMSR，在一个做市交易的市场中，做市商定价公式为：

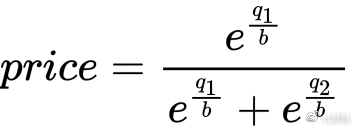
常量参数 b 与做市商可提供流动性大小有关，可以为任意常量：b 过小则价格变化敏感，即很小的交易量就可以造成价格变化明显；b 过大则价格发现迟钝，即很大的交易量才可以使价格发生明显改变。因此对于一个小型不频繁的交易市场，b 一般取小值，对于大型交易市场，b 取大值。q1 和 q2 分别表示交易市场中两个币种流通数量，如果有多个币种，可以继续增加 q3, q4...。举个例子，在一个市场中有 10 个 A token、20 个 B token 以及 23 个 C token，假定 b=10，则此时 A 的定价为：

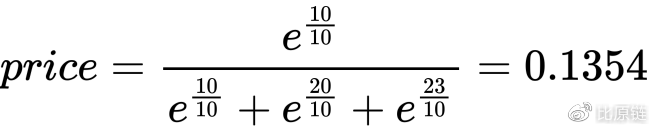
做市商可以根据公式设置初始数量，给每个币种设定价格和汇率比。之后的定价将完全交由每一笔交易行为按照公式对状态的更改，所以我们还需要一个成本函数（Cost Function）。对于函数做市机制，有两个重要函数，一个是上面的价格函数，另外一个是对应的成本函数：

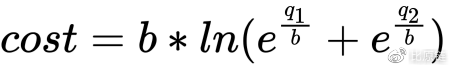
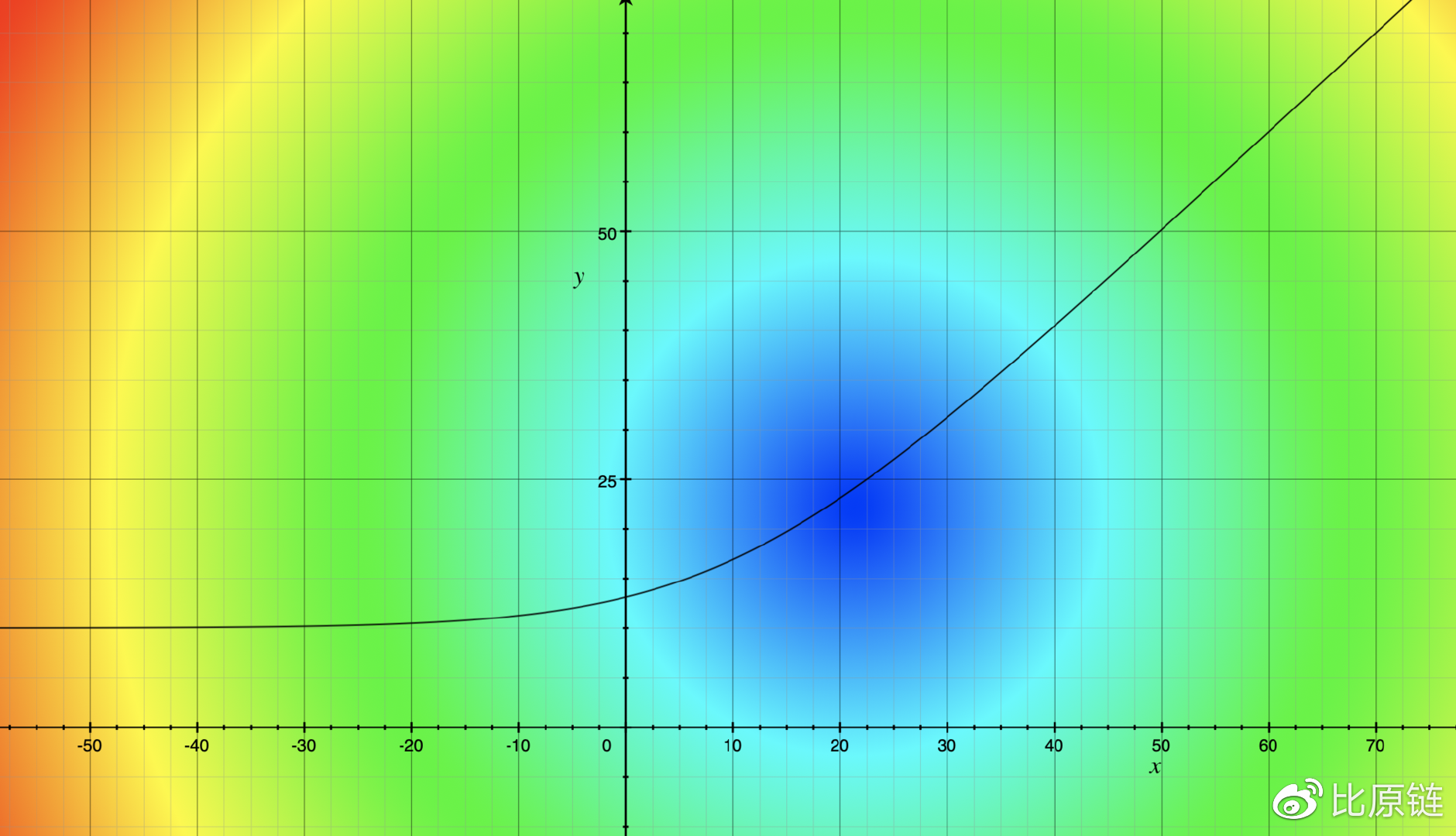
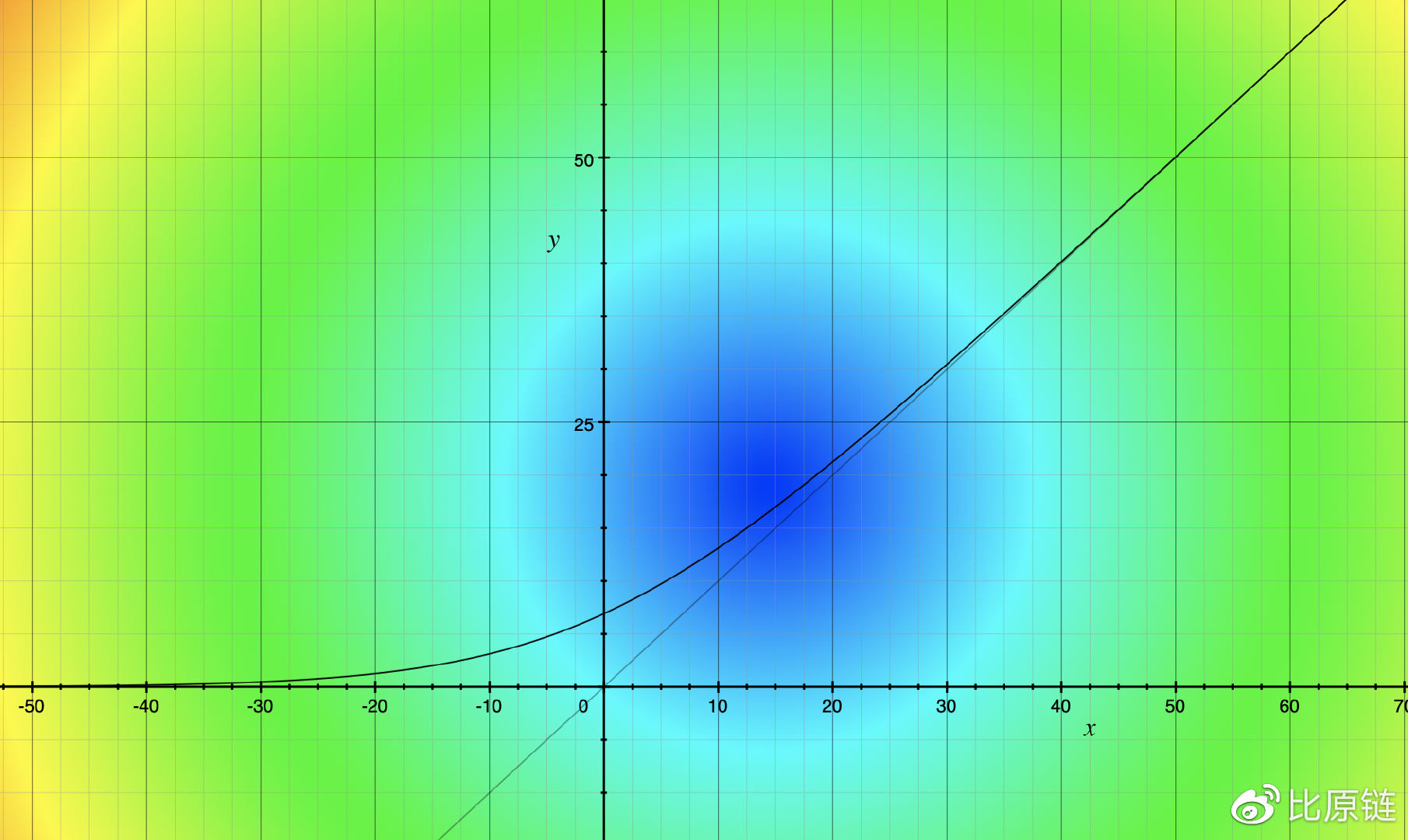
（注：这两幅图是对成本公式的举例示意。左图表示两币种都有流通，并假定其中一种未进行交易，只考虑另外一种随着交易数量的变化其成本的变化曲线，x 增大表示在购买该币种，随着 x 增大，成本增率变大，最终稳定在一个恒定状态；右图表示市场中只流通一种币的交易成本曲线与最简单的一元一次严格增函数的对比）

成本函数用于计算交易者跟做市商间进行一笔交易所付出的成本，即交易买卖是有摩擦的，最直观的直觉是，购买某种币越多，付出的成本越大，即需求越多，价格越高。例如在一个三币种的交易市场里，当前有 10 个 A token，20 个 B token 和 23 个 C token，我要购买 7 个 A token，需要付出多少成本？根据成本公式计算交易变更前后的状态，变更前：

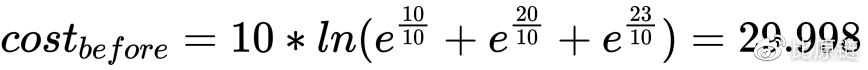
交易后更改状态有：

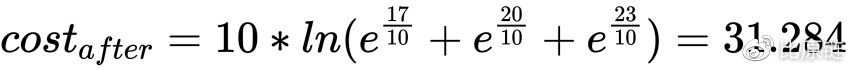
我付出的成本即为二者之差 31.284-29.998=1.286（根据实际场景对该数值进行倍数相乘得到对应的金额）。同理来看卖出的场景，假定此时 D 的数量为 50，E 的数量为 10，定义 b=100，我向做市商卖出之前买入的 10 个 D token，则做市商应给我：

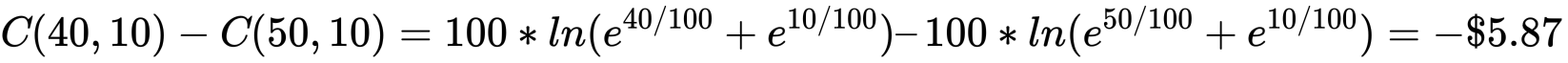
我在系统初始时向做市商以低成本买入 10 个 D token：

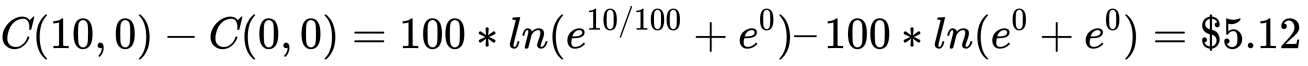
一来一去，我净赚 5.87-5.12=0.75 美元。

基于此，我们进一步拓展到数字货币交易对场景中。假定做市商提供两种币间的兑换服务，比如 BTM 和 ETH，用户要购买 BTM，需要向系统投入 ETH，即用户售卖 ETH，系统返还 BTM，这可以拆成两步操作，先向做市商售卖 ETH 拿到钱，再用这些钱向做市商购买 BTM，最终获得的 BTM 数量即反映了汇率比或者成本，所以我们有：

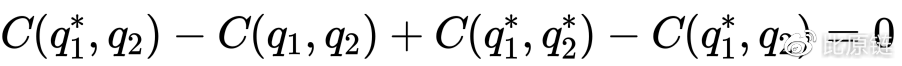
可以得到公式：

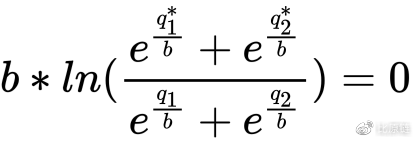
其中只有 q1* 和 q2* 是未知量，可以用 x 和 y 来代替，作图直观表示出 ETH 和 BTM 的兑换曲线（图中黑色线，浅色双线为双曲线）：

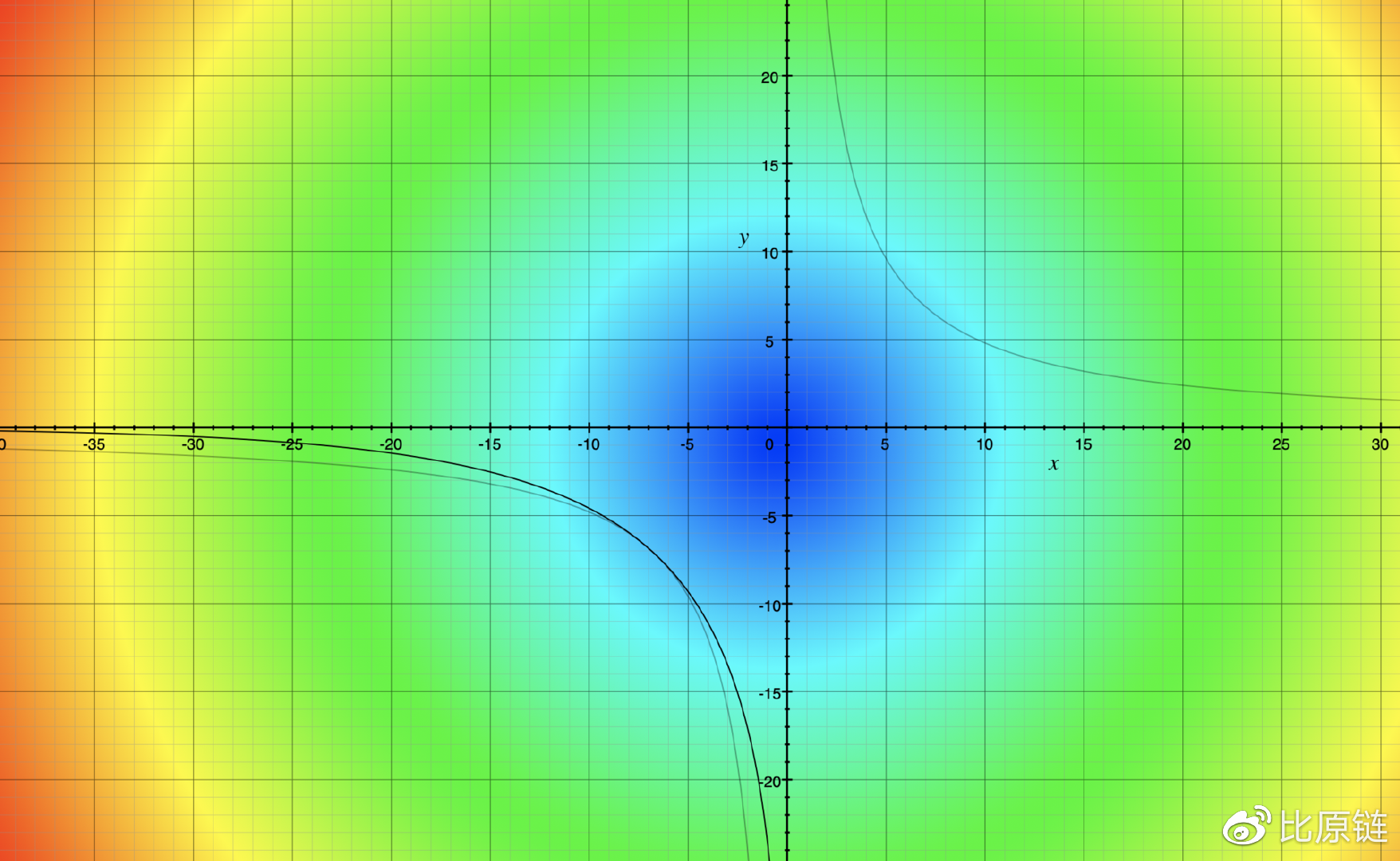
这就跟我们常见的恒定乘积做市商（Uniswap 双曲线）很贴近了。进一步我们拓展到三维甚至多维空间（如同 Balancer 一样），如图呈现其三维曲面形态：

LMSR 为自动化做市引入了非常优美的函数变化曲线，完美解决了供需与价格难题，最终慢慢演变成 CFMM，被加密货币行业广泛采用。从某种意义上讲，曲线之美缔造了强大的金融自动化做市机制。MOV 超导也是根据 LMSR 基本原理和目前常见的 CFMM（如 Uniswap、Balancer、Curve.fi）项目进行了进一步的创新和实现。概括起来有如下几点创新：

（1）构建更为灵活的适用于稳定币间兑换市场的 CFMM 函数以及关键参数；

（2）不局限于二维函数模型，可灵活调整到多维几何空间，即支持一个储备池中存在多个币种间互相兑换，并解决存入单一资产问题；

（3）通过引入计息规则，完善当前 CFMM 手续费和收益计算模型的不健全，并基于凸优化为套利者提供高效的套利策略模型；

（4）全面风控指导，尤其是外部市场波动风险，包括 LP 的无常损失（Impermanent Loss）、滑点保护机制、被套利问题等。

MOV 超导基本架构

超导基本角色

MOV 超导基于储备池提供流动性，所以也可以称之为储备池做市商，由【 流动性提供者（LP） 】这一角色向储备池按照当前币种间正常市场汇率比例投入各资产进行做市，LP 会因此获得系统收益，收益来源便是【 正常交易者 】在此市场交易产生的交易手续费。这个市场的定价或者维持汇率锚定并不是通过传统的中心化预言机机制，而是完全依赖于一种【 套利者 】角色，一旦因为交易或者外部汇率变化导致场内汇率跟正常值出现明显偏差，套利者便会迅速进行套利操作，在场内以低成本换取偏差代币，然后去场外汇率正常的市场高价卖出，赚取额外收益的同时将场内汇率“搬”到跟场外一样，这种通过不断的高频套利维持场内价格与正常市场汇率锚定的机制，我们也称之为链上预言机，这也是 CFMM 最为重要的意义之一。

在这样看似简单的过程中其实蕴藏着复杂的套利与损失问题：有些 LP 可能并没有严格按照理性比例存入各资产；场内价格严重偏离外部正常市场汇率；迅速波动的外部市场环境对 LP 存入策略的影响；超级攻击，例如闪电贷攻击。简单来概括这些问题的本质 —— 被套利者利用，加大 LP 的损失，不利于系统健康运转。但如果我们的系统和机制设计可以很好地解决这些问题，让套利者成为一个“白帽子”套利者，而不是像黑客一样利用系统金融漏洞进行恶意套利，不仅有助于维持场内汇率跟外部正常市场汇率间的无缝锚定，创建一种完备的链上预言机和去中心化交易市场，更有利于系统中所有关键角色（LP、正常交易者、套利交易者）达到一个共赢的平衡（每个角色都持续获得正向收益），让系统正向壮大。

除了这些关键角色外，还有一些辅助设施，比如单一资产代理转换，即帮助存入单一资产的 LP 转换成按理性比例存入各资产的机制（后面会讲不按照理性比例存入各资产的损失问题）；滑点保护机制，帮助正常交易者和 LP 规避损失；黑天鹅熔断机制，以防某种稳定币出现黑天鹅信用危机造成的系统风险；外部市场波动监控，通过灵活调整系统关键参数应对极端的市场行情波动。

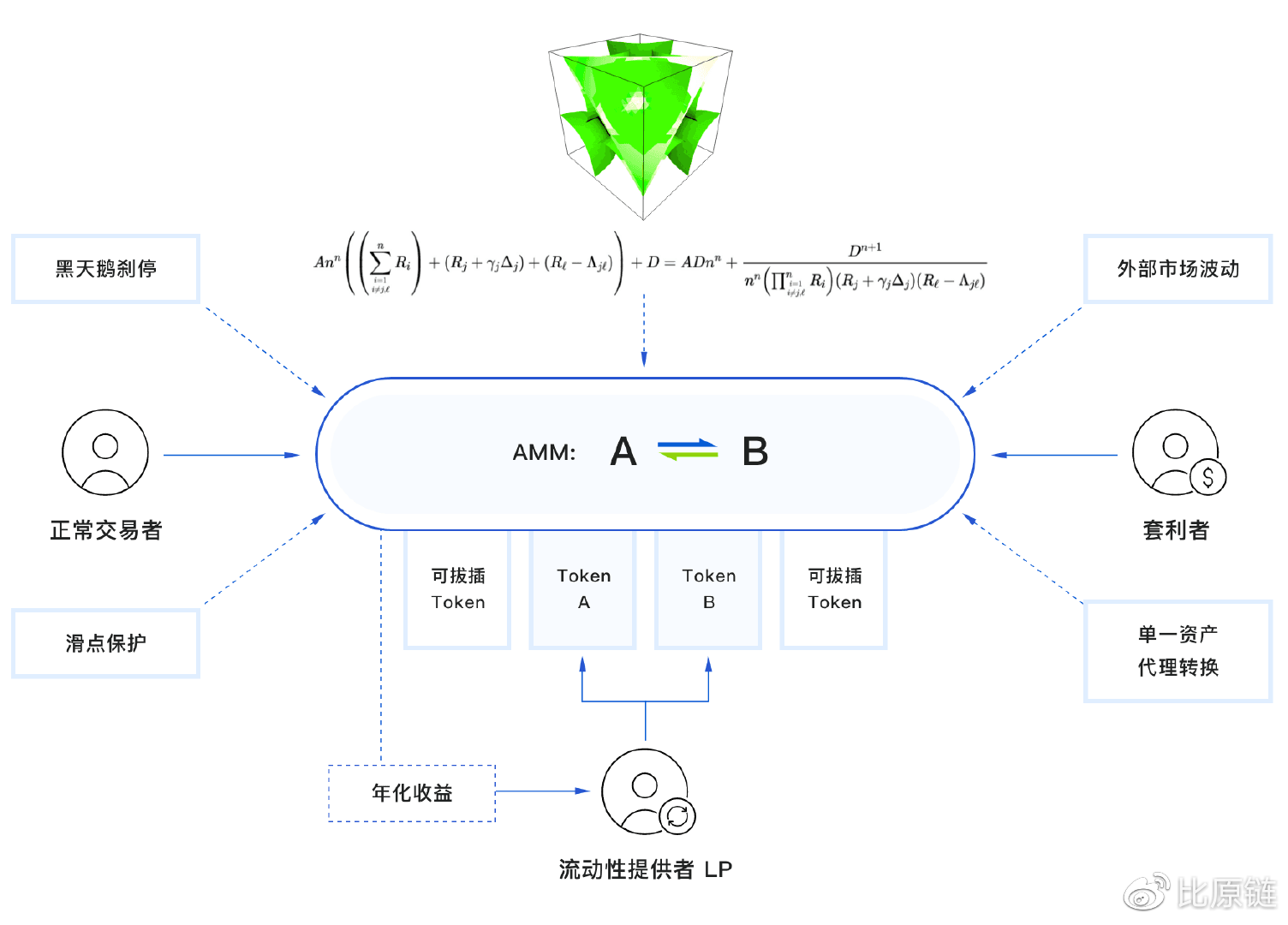
MOV 超导角色图

核心函数公式

随着 DeFi 的崛起和壮大，越来越多的稳定币交易需求从 CeFi 交易平台转向更为简便、安全、透明的 DeFi 交易平台和钱包，很多稳定币还涉及到平台间的竞争以及合规问题，因此并不适合单一的中心化交易所，这也是 DeFi 交易平台能够有机会跟中心化交易所竞争一席之地的机遇，而 CFMM 机制天然适合稳定币兑换生态。因此 MOV 超导首发的是稳定币间的交易兑换市场，这里我们将还原如何构建出适合稳定币兑换场景的 CFMM，也是超导最为核心的技术。

我们先来看最简单的做市函数 —— 恒定之和：

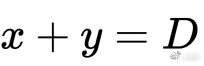
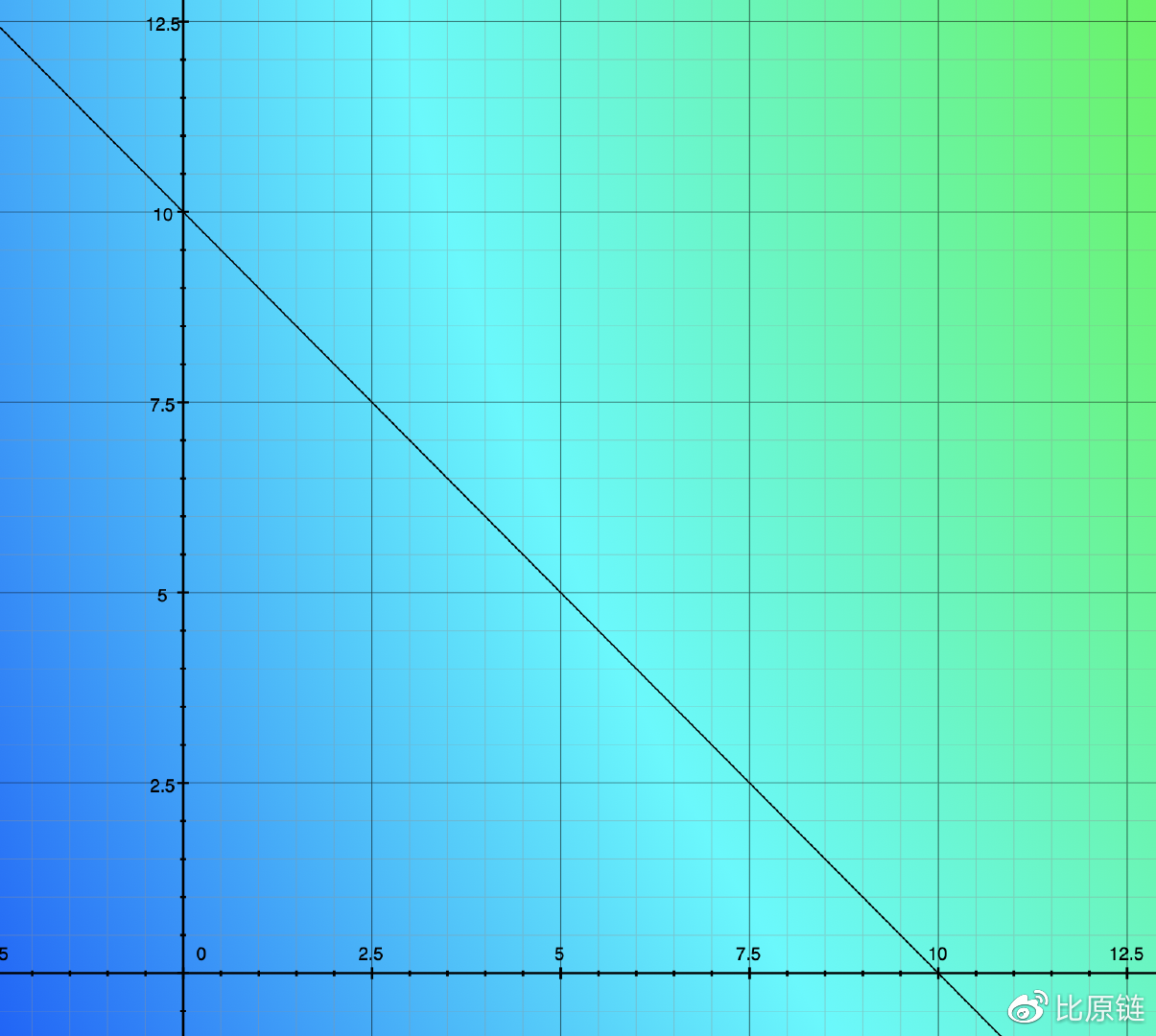
上图示意我们初始时有 5 个 USDC 和 5 个 USDT。在这条斜率绝对值恒为 1 的直线函数做市下，USDC 和 USDT 间的兑换汇率始终保持为 1:1，即 1 USDC = 1 USDT。看似很完美，但是有两个致命问题：

（a）流动性枯竭。在没有强制干预的前提下，很容易出现一方数量归零，将无法再次提供流动性；

（b）无法适应变化的汇率。在外部市场中，稳定币间并不会完全 1:1 锚定，每种都有可能出现各自的波动行情，场内需要能够实时锚定，否则会带来套利危机。

为了弥补缺陷，我们很自然的想到了著名的双曲线函数（已被 Uniswap 在实际场景中验证）—— 恒定乘积：

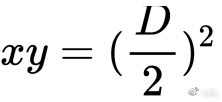
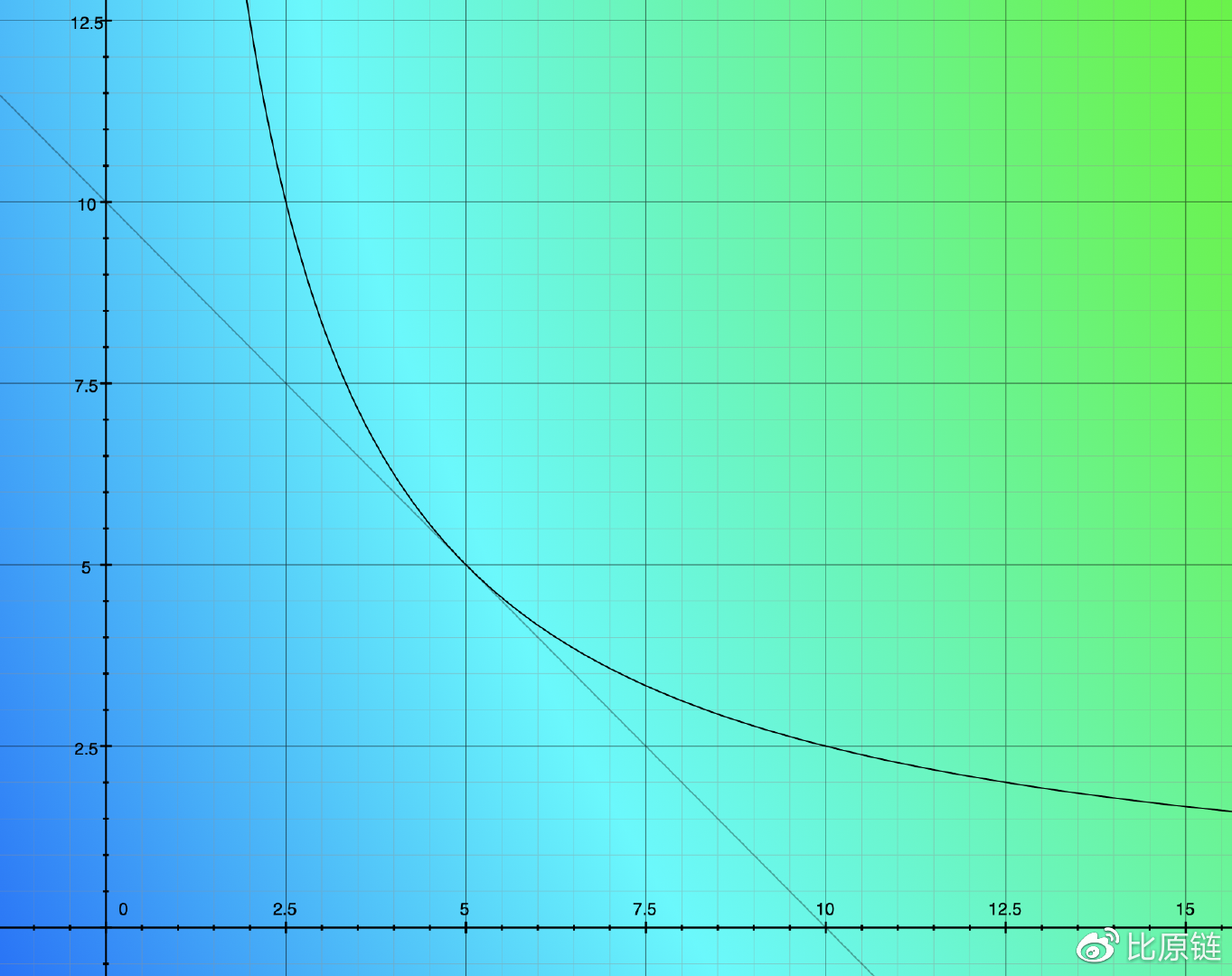
（注意：这里双曲线的恒定乘积值应该根据 x+y=D 来定，双曲线切于直线，初始时两种币数量相等，保障汇率为 1:1）

双曲线最为直观得反应了供求与价格的关系。其函数曲线无限接近与 x 和 y 轴，但永不相交，即当一方代币因为极度需求导致池中数量越来越少，则其价格接近无穷大，两币数量比即为汇率，也即双曲线对应点斜率。这条曲线完美解决了上述两个难题，但同时又引入了一个新的致命问题：无法适应稳定币兑换场景。稳定币大多数情况下汇率是稳定的，而且接近 1:1，双曲线函数会引入很大的滑点，即便在很少的交易量下，因此不利于满足大额稳定币兑换的需求。

能否将两个函数各自的优势结合到一种新函数中 —— 稳定的汇率输出、极低的交易滑点、可自动调节的场内汇率以及无尽的流动性保护。从图像直觉上（如上图），我们其实在寻找一条在两条曲线之间的一种曲线，既能够在中间位置贴近直线，又能够在尾端向双曲线一样无限贴近坐标轴。在几何数学上，要获得两曲线之间的线只需要将二者的表达式相加（如下图中黑色线）：

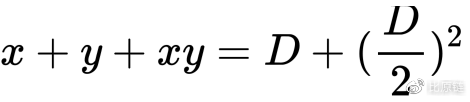
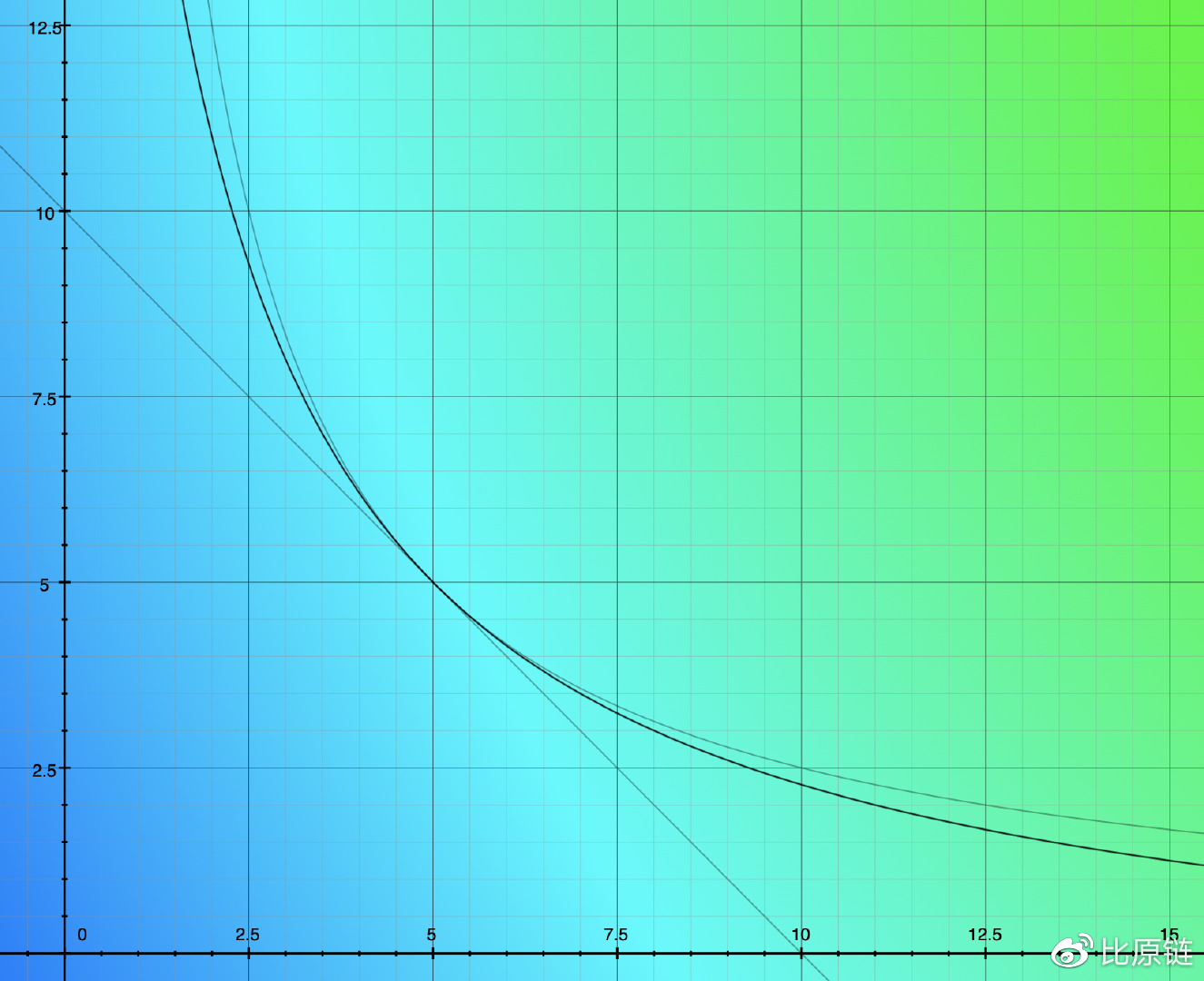
还不够贴近直线表达式。可以赋予权重常量：

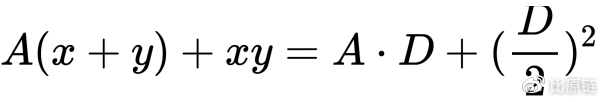
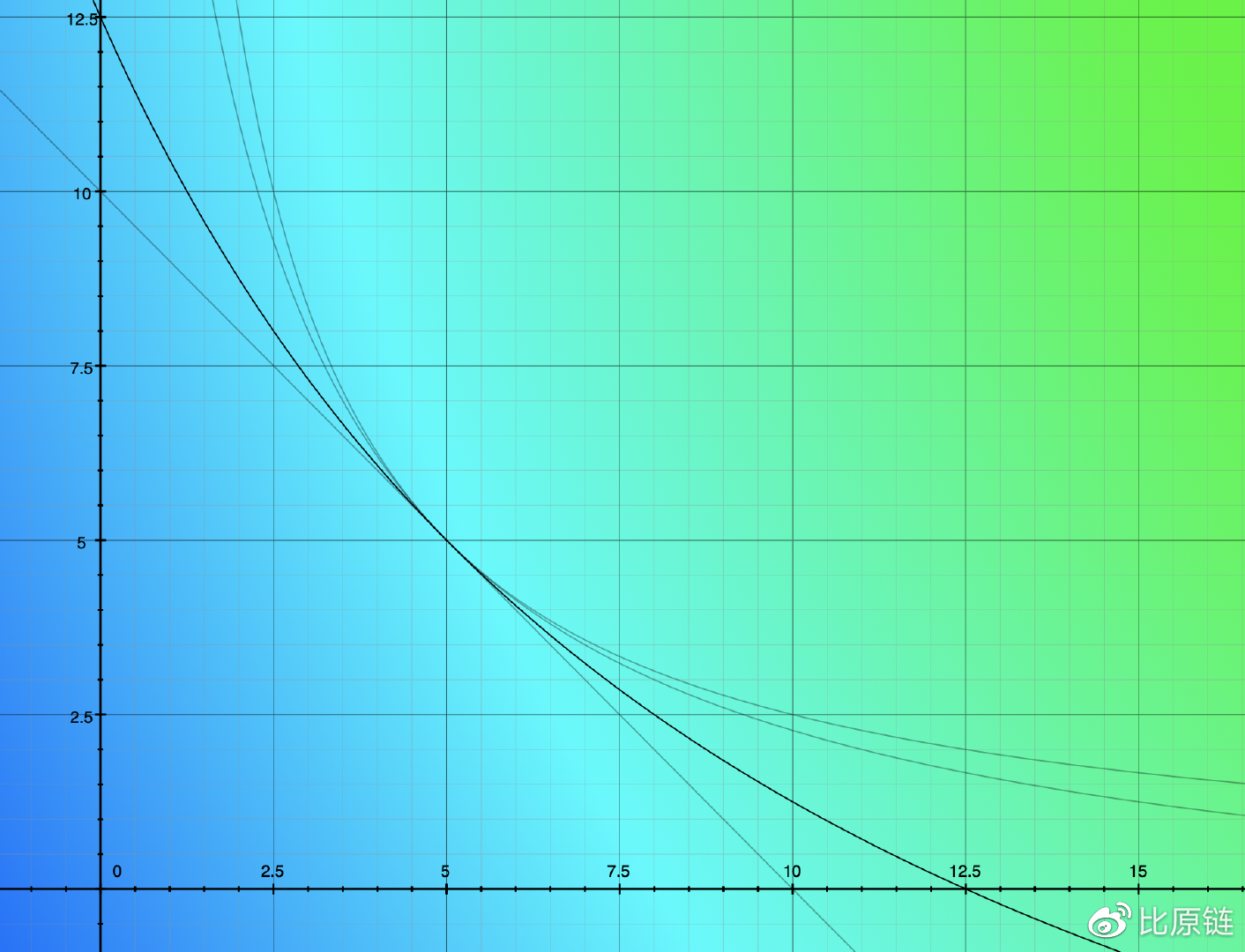
赋予 (x+y=D) 以权重 A，A 越大表示合成曲线比例越以直线为主，即偏向直线形态，但同时我们发现合成线的尾部并没有延续双曲线的优势，也就无法提供无尽的流动性。这里我们需要用极限思维和逆向思维来推导合成公式可能的组合形态（如下图中黑色曲线） —— 我们以初始化点（D/2, D/2）为中心，在中间范围极度贴近直线，坐标的乘积（即x*y，矩形面积）虽然不再等于双曲线恒定乘积值 (D/2)^2 —— 比之小，但越往中心越接近 (D/2)^2，越远离中心越小于 (D/2)^2。直到极限位置（即合成曲线无限贴近坐标轴），x*y 将远远小于 (D/2)^2，逼近于0。

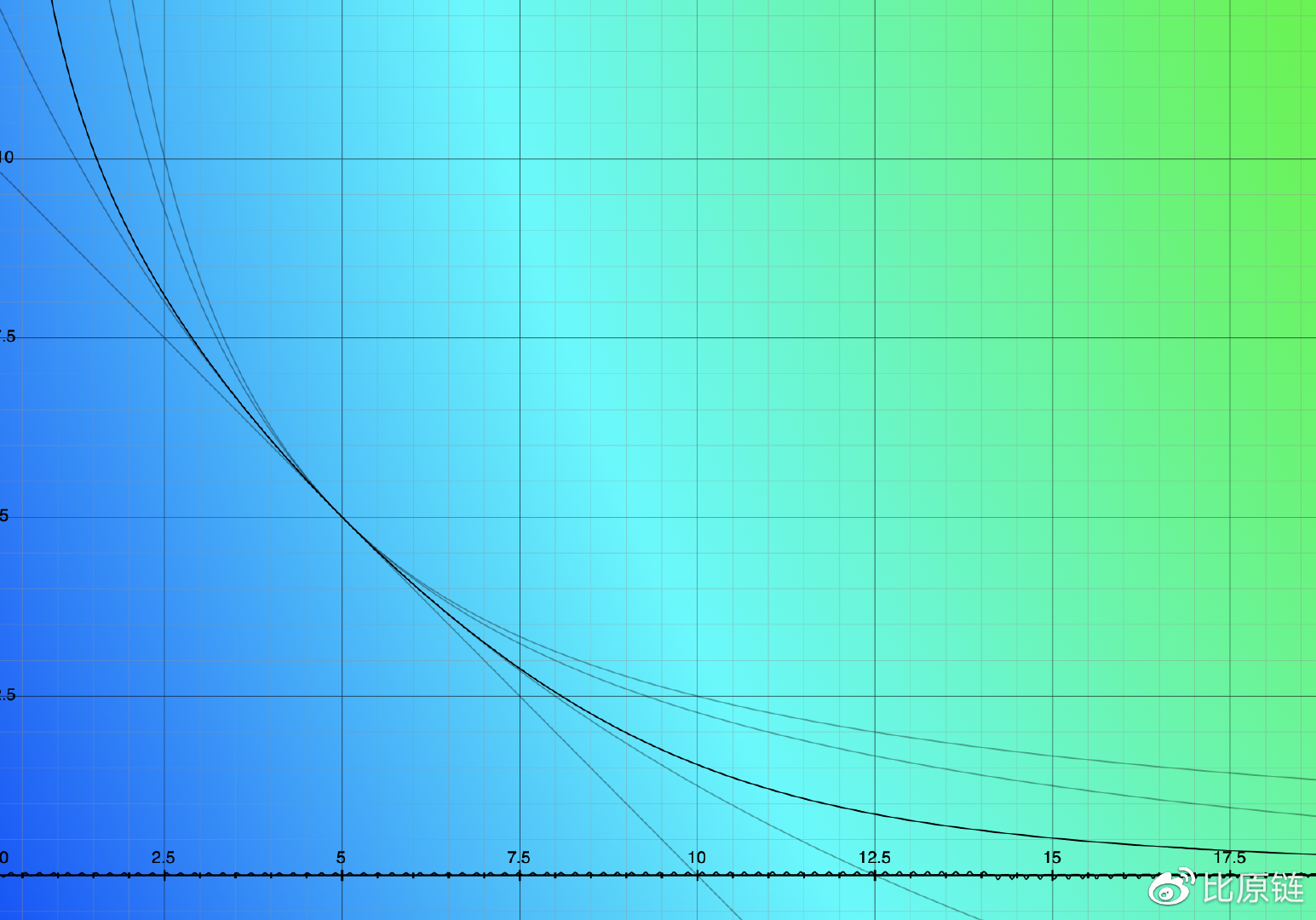
所以我们的表达式应该满足上述特征。在上面权重表达式的基础上，我们让 A “动起来”，成为变量 X —— 当线上的点越贴近中心位置，X 越趋于 A，使得合成表达式权重偏向直线；当线上的点越远离中心位置，X 越趋于 0，使得合成表达式权重偏向双曲线。因此得 X：

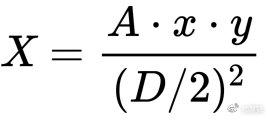
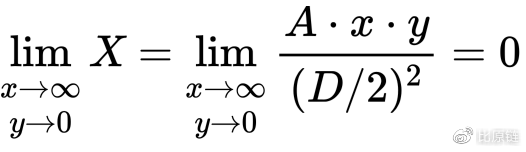
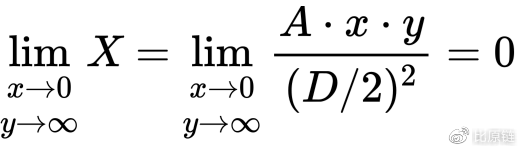
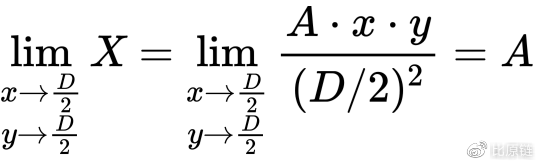
至此便可以构建出完整的合成函数公式：

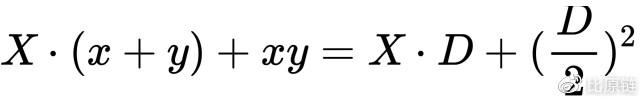
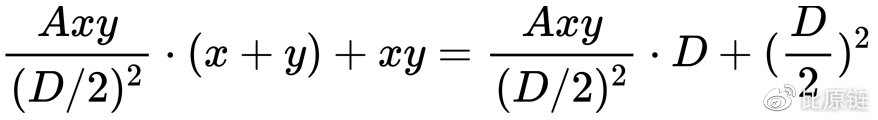
化简得：

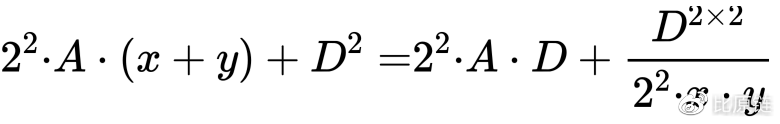
以及函数曲线为（黑色线）：

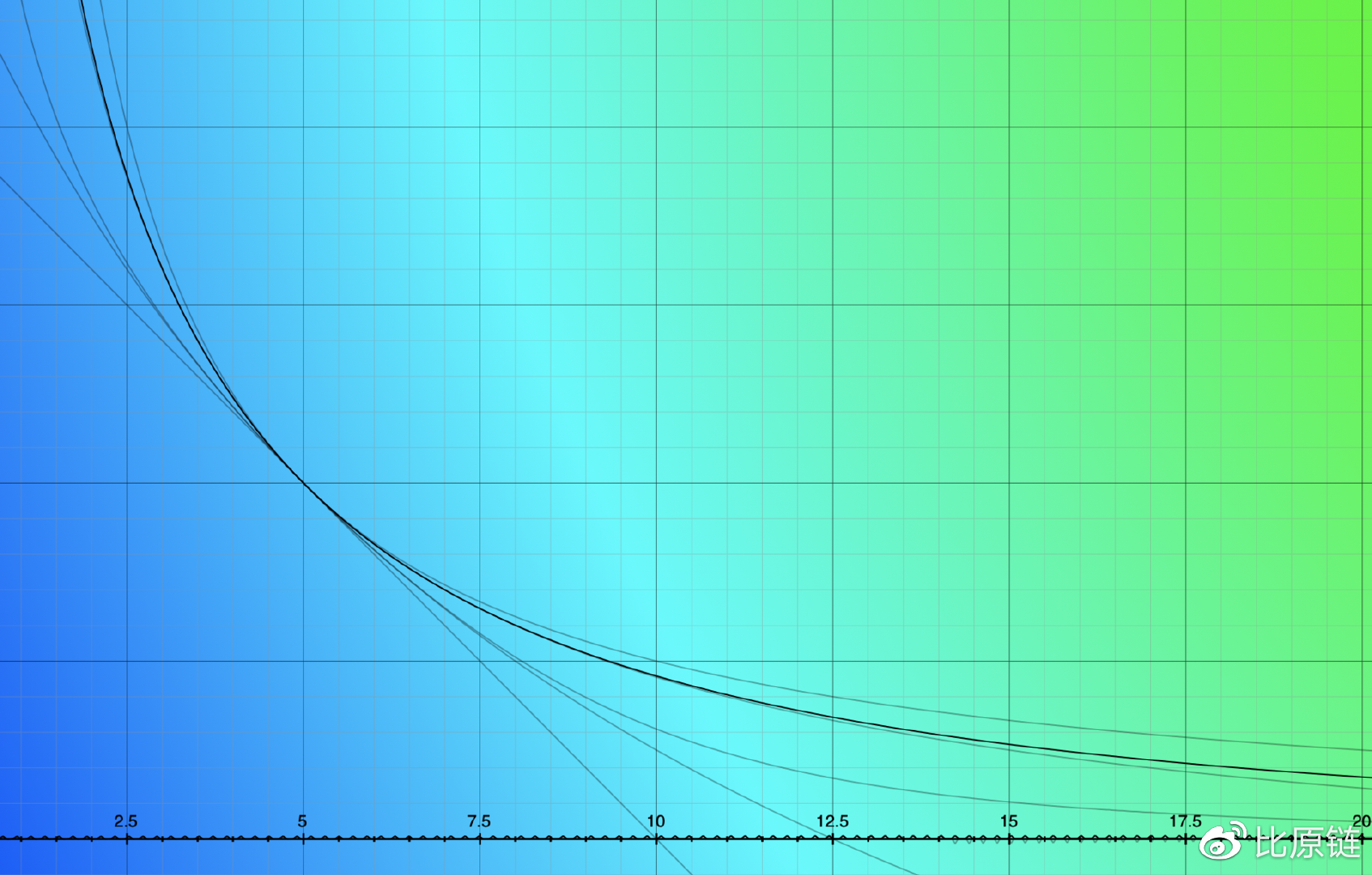
如果继续追求完美，我们受到了 Curve.fi 的启发，权重变量 X 乘上一个可以表示直线和双曲线在坐标轴上位置的常量值 D —— 如果流动性越大，则对应的直线和双曲线的 D 值越大，两条曲线越“膨胀”，相应的权重常量也应该跟 D 的膨胀保持同步，才能“咬住”贴近直线，因此确切的应该是 —— 当线上的点越贴近中心位置，X 越趋于 A*D（在随后的多维拓展中，还应该把维度考虑进去，即 A*(D^n)），只有这样才能随着流动性增大自动放大权重，否则一直维持 A 的上限，将会随着流动性越来越大而不再“贴近”直线，失去恒定。最终我们得到完美的核心公式如下：

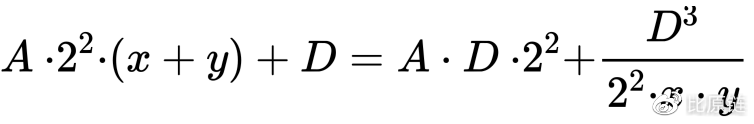
以及函数曲线为（黑色线）：

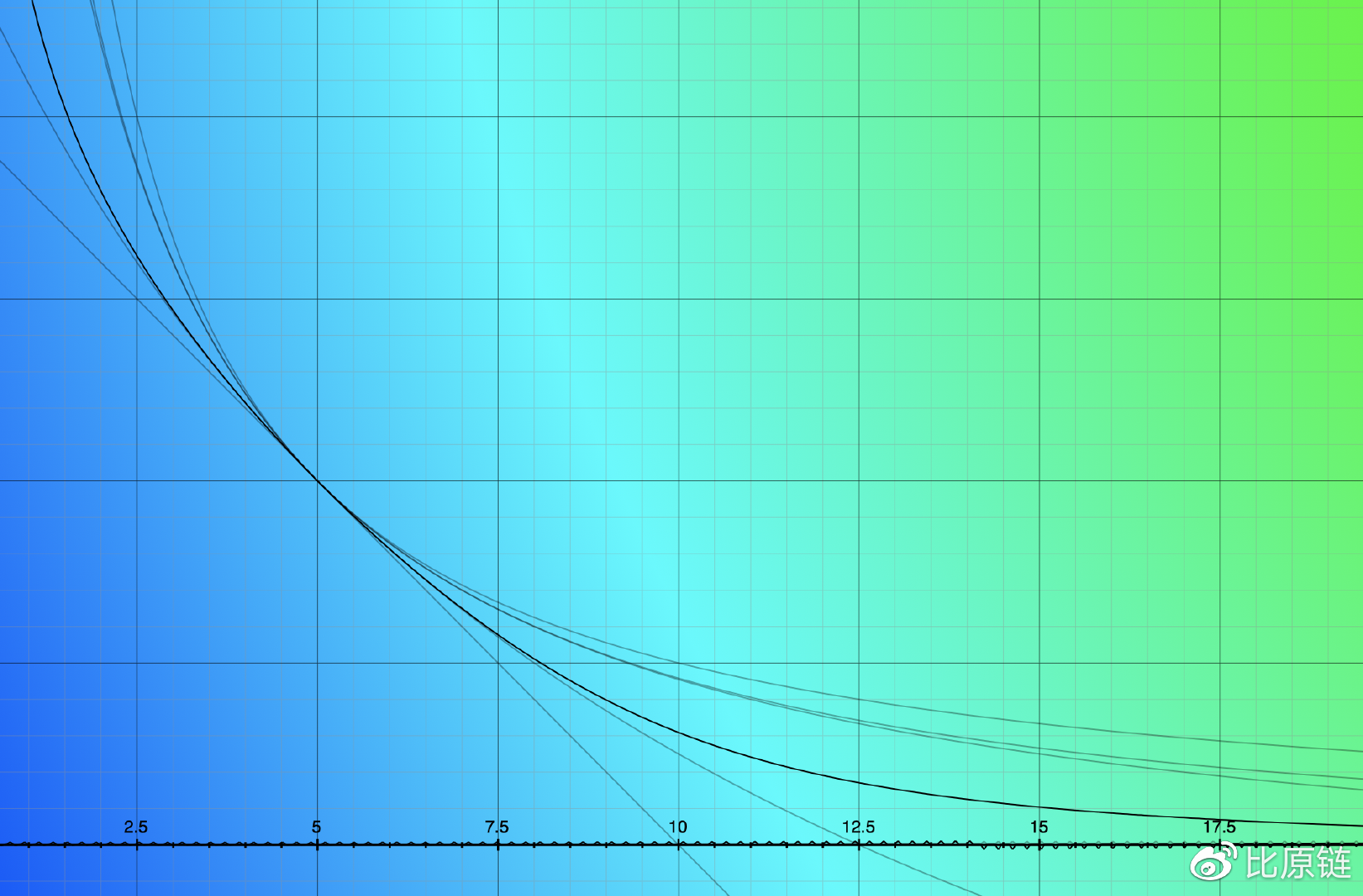
（注：确实要比权重不乘 D 要优越）

借助两币种示例，我们找到了构建核心公式的基本原理，同时兼得了中心范围超低滑点以及尾端无尽的流动性两大优势。下面我们给出多维标准核心公式，本质是一种隐函数：

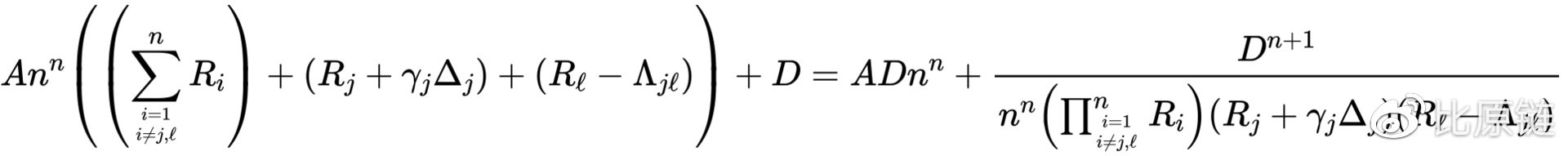
（注：假定手续费为 ρ，即当用户用一定数量 ∆x 的 A 币换取 B 币时，需要在扣除手续费比例的 A 币后再将剩余数量的 A 币投入计算公式，即 (1-ρ)∆x ，若令 γ=1-ρ，则为 γ∆x。）

常用的二元形态为：

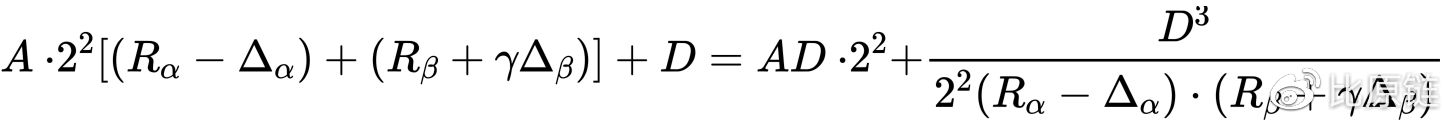
其中，

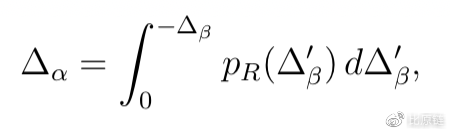
为了方面直观感受，下图给出一种三维形态示例图（蓝色表示恒定乘积曲面，绿色表示恒定之和曲面，中间是我们的核心公式在三维空间下的形态）：

这里要特别指明所谓的多维仅仅是核心表达式可以兼容多种变量，即多个币种，但在同一时空下存在的仅仅是两两间互兑，不存在三者及以上兑换，否则将会升维到真正的多维空间，即便在三维空间几何中我们也无法规划出曲面上最优的点移动轨迹（代表三币种间同一时空互兑带来的最优路径），而到了四维及以上空间更无法按照常规手段完成多币种间轮兑。实际交易场景中也是两两兑换居多，因此本质上我们是对多维核心公式进行了降维求解 —— 即只将在兑换的两种币数量视为变量，其他币种数量视作已知常量带入核心公式（因为两者间互兑，并不改变其他币种的数量），将多维公式降维到二元分式方程，通过牛顿迭代法，根据输入的币种数量求得要换的币种数量，完成交易成本计算。同理跟 LMSR 一样，成本函数也对应着汇率公式。

对于二元核心公式，求曲线上点的切线的斜率，即代表此时场内对应的汇率，问题简化为对隐函数求导。

注：对于隐函数的导数，采用隐函数求导法来求函数的导数 —— 将方程两边对 x 求导，在求导过程中，将 y 看成 x 的函数，运用复合函数求导法，从而求得函数的导数。 二元相对简单，多元的需要求偏导数。

对于多维核心公式，依然采用降维分析，例如对于上面的三维曲面，求此时点所在的切平面分别相对于三个坐标平面的相交线的斜率，即代表两两间的汇率，同样把计算问题简化为对多元隐函数求偏导数，即对多维核心函数进行隐微分得如下一元方程：

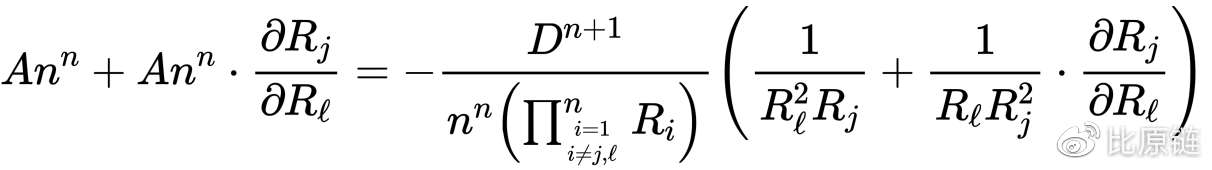
我们所求的汇率即为：

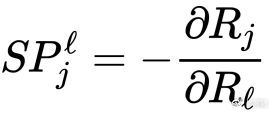
进一步，我们定义 j 币和 l 币是在兑换的两种资产名，j 币的数量为 y（即替换上面的 Rj），l 币数量为 x，定义两者的汇率表示为 SP，对上面原始公式移位化简，得汇率 SP 的标准公式：

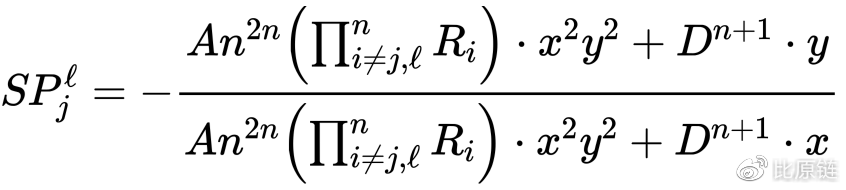
此公式适用于资产池中资产种类在三种及三种以上的情况，也是最普适的汇率计算公式，公式右边所有变量都可知，即根据此时资产池中各资产现存的数量进行汇率的求解，x 和 y 是兑换两资产各自在池中现存的数量，括号中的累乘积表示的是除了 j 和 l 这两种资产外其他池中所有种类的资产的数量的乘积，都是已知变量。n 代表资产种类有多少，A 和 D 是核心公式常数。对于只有两种资产的池子，可以对上式进行进一步化简，去掉括号累乘积项（注意是去掉该项，而不是令该项等于 0），然后令 n=2，得如下两资产池汇率计算公式：

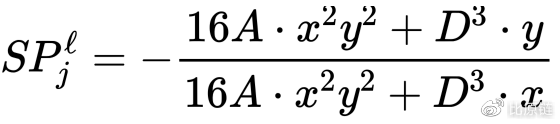
至此我们完成了所有核心公式的构建！

LP的损益模型

我们认为对于一个 CFMM 市场，除了核心公式，最为重要的就是流动性提供者的损失和收益问题，而判断一个 CFMM 市场是否具有吸引力和抗风险，也正是看其是否全面刻画了 LP 的损失和收益模型，总结下来模型应该包含如下几点：

（1）无常损失（impermanent loss）模型；

（2）不按理性比例同时存入各资产，包括单一存、场内汇率与外部市场脱锚时存、存入过程由于干扰、抢先交易和时间等因素导致的比例出现偏差；

（3）稳定币 CFMM 独特的被大量套利问题以及极端套利保护机制；

（4）针对 LP 的滑点保护机制；

（5）手续费收益重新注入流动池及手续费模型；

（6）LP 的年化计息模型以及提取操作。

我们依次来讲解。

（1）无常损失 。这是大多数的翻译，其实本质上应该叫做临时损失，或者叫虚损失。这是由于 LP 在投入资产后，在没有手续费收入时，面对市场波动和汇率变化，会被套利者不断套取资产，导致自己所占有的池中资产总价值比刚投入时变少了，但是等汇率又回到投入时的汇率时，这部分损失又消失了。对于简单的恒定乘积做市函数，我们可以很容易刻画出无常损失曲线。

假定 LP 刚投入时有 xy = D，当汇率发生变化，套利者进行套利后数量变为：

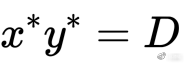
定义无常损失表达式：

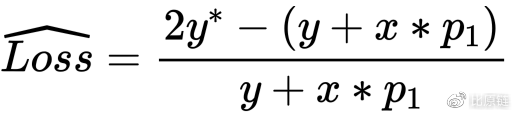
其中有，

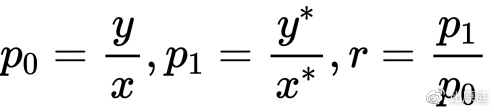
根据 r 表达式，代入 p0 和 p1，化简得：

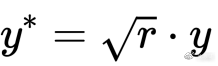
另外有：

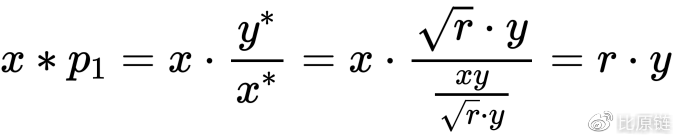
最终都代入获得无常损失关于汇率变化幅度 r 的函数表达式：

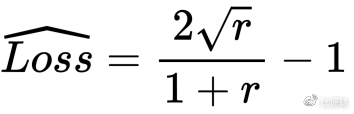
对应函数图像：

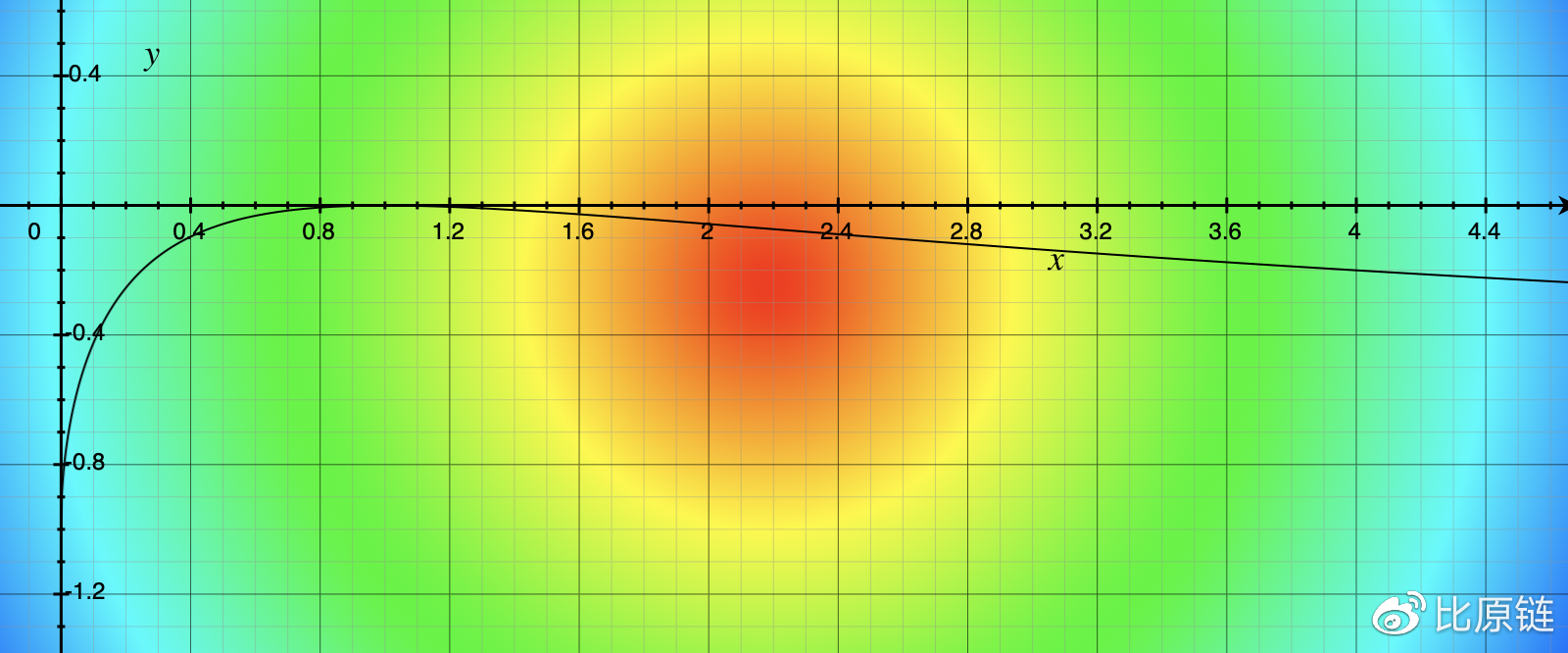
从图像上可以直观看到，不论之后汇率是涨还是跌，都会给 LP 带来无常损失，跌带来的损失更为显著和迅速，当汇率涨到 4 倍时，大约会带来 20% 的损失。

再回到我们的超导核心公式，由于隐函数过于复杂，很遗憾我们没法像上面化简过程一样进行无常损失表达式的构建，虽然无法用公式量化无常损失，但机制跟恒定乘积函数是一样的，不论汇率涨还是跌，都会带来无常损失，所损失的即为套利者所套利的，因此可以从套利者获益的角度反向推算 LP 所经受的无常损失范围。一般情况下的无常损失有助于激励套利者搬平场内汇率，但我们需要帮助 LP 尽量规避过度的无常损失，通过官方主动快速套利的机制，将所套利重新回馈给 LP。

（2）按比例同存同取 。前面我们提到过，LP 不按照理性比例存入资产会给自己带来被套利损失。在理解了无常损失问题后，我们可以发现所谓损失的本质就是被套利，而被套利来自于 LP 存入时的比例与当下理性的市场汇率不一致。可以用函数图像来直观感受：

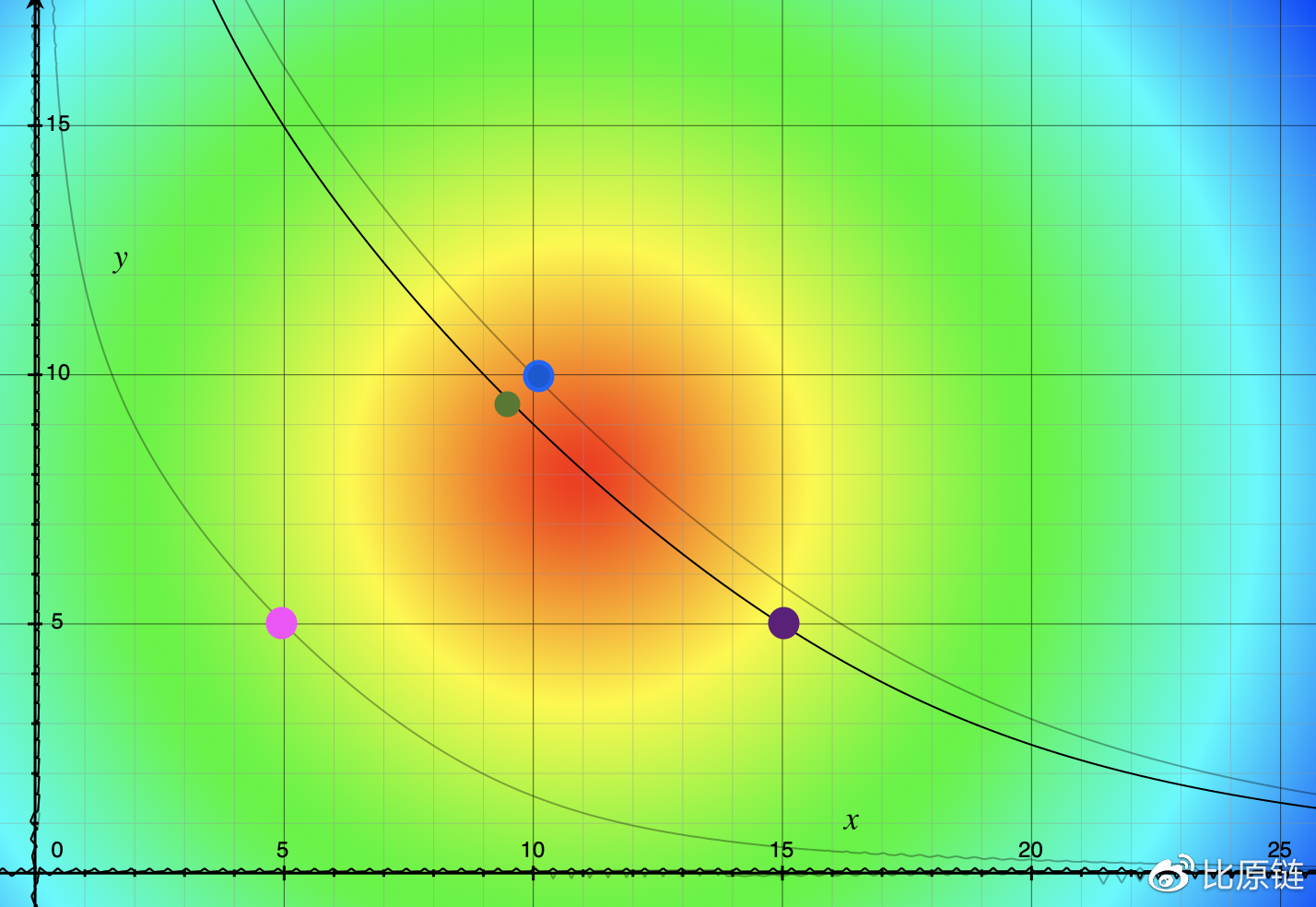
上图示意：最下面曲线代表最初的状态，粉红色点也代表当时池中的一个理性资产比例，即 USDT:USDC=5:5，如果一个用户有 10 美元，他应该将 10 美元变成 5 USDT 和 5 USDC，同时存入池中，最上面的曲线即为变更后的公式，而此时曲线上的点位于蓝色位置，即池中 USDT:USDC=10:10，维持了汇率恒定，所以不存在被套利空间，也就不会有损失；但是如果该用户的 10 美元全是 10 USDT，并一次性投入池中，我们将得到中间的曲线公式（该曲线表示的流动性大小要小于最上面曲线），而且此时曲线上的点位于紫色位置，即池中 USDT:USDC=15:5，明显偏离正常市场汇率，会被套利者瞬间利用进行套利，将点搬移到图中绿色位置，即池中 USDT:USDC=9.5:9.5，该 LP 为套利者进行了无偿奉献。

这里要注意的是，此损失仅仅来自该 LP 的资金，并不会影响之前其他 LP 的可提取资产值，如图所示，当套利者搬到绿色位置后，该用户如果全部提取自己的资产，将只能提取到 9 美元，而非存入时的 10 美元，套利者拿走 1 美元，之前的 LP 不赚也不亏。如果紫色点还没来得及被搬移到绿色点，在该 LP 之前的 LP A 要提取自己的资产，则 LP A 也会攫取部分套利。在后面的计息模型中我们会详细讲解其中的计算法则。

这里我们只是举例了一种简单的模型，即整个过程中汇率维持恒定，不存在外部市场波动，而在实际生产环境中，外部市场汇率高频波动、存入过程扰动误差、LP 不按理性比例存、套利者攫取、之前 LP 提取流动性等这五要素会复杂交融影响，很难凭直觉判断 LP 资产存入策略是否规避了损失。但我们对于 LP 最直接的忠告是，实时关注场内汇率与理性市场汇率，只有在二者极度接近以及恒定锚定时，再严格按照比例投入自己的资产，才能将损失降到最低；避免在某种稳定币资产遭遇频繁外部市场波动时存入。

这也让我想起了分布式一致性系统的设计和开发过程，原理或者核心公式其实非常简单，但正是这些复杂的不可预测的外部因素以及路径，导致了系统的复杂度和风险度无处捕捉，因此人们开始用 CAP 和 FLP 指导自己的系统设计，同样在我们的 CFMM 市场中，一切也才刚刚开始。

（3）被大量套利问题以及极端套利保护机制 。接着第二个问题的解释，我们列出几点会对系统带来过度损失的模型：

a. 在初始化时，创始 LP 以 1:1 投入稳定币资产，随后在市场和套利行为下，不断让场内汇率更新，直到实时锚定到市场汇率，如果外部市场汇率因为极端行情等因素明显偏离 1:1，由于超导曲线前半段优越的抗滑点特性，在滑动到市场汇率的过程中，可能会存在路途过长，导致套利者攫取大量套利利润，严重损害创始 LP 的利益。因此对于一个成熟的稳定币 CFMM 来说，必要的极端套利保护机制是需要时刻准备的，由官方套利者及时接手过度套利空间，之后将利润返还给 LP。

b. 市场汇率在波动的同时，流动性池大小也在不断的增加或者减少，套利者如果故意不及时套利锚定外部市场汇率，让场内汇率一直存在偏差，会造成 LP 持续按照偏差比例存入资产，最后套利者在积聚到一定量后开始一次性套利，给这些 LP 造成大量的套利损失。

除了官方提供的极端保护机制外，我们也鼓励 LP 担当套利者，他们能够清醒地判断场内汇率是否出现偏差，抢在恶意套利者之前搬平场内汇率，不仅给自己存入资产规避损失，也带来额外的套利收益。

所谓的理性比例是指跟市场汇率锚定，而不是任意时刻流动池中的资产比例。假设市场汇率是 1:100，场内此时出现脱锚1:105，则 LP 需要先抢在套利者之前完成套利和市场平衡，再按照1:100 投入资产，如果不先完成套利，不论是以 1:105 还是 1:100 存，都会被套利产生损失。我们更倾向于 LP 也能充当市场预言机和套利者，在承担场内外汇率平衡的责任的同时，也可以获得套利收益，也是为了自身损益的考虑，避免无谓的损失。

（4）LP 的滑点保护机制 。滑点保护是对正常交易者和 LP 的保护。在 LP 情境中，即便 LP 再理性和认知及时，也可能无法规避不按比例存的风险，比如在提交上链的过程中，出现了抢先交易、操作失误或者极端的市场波动，因此无法保障时序原子性，而我们的滑点保护机制会检测 LP 的范围超出，在微小范围内允许 LP 继续存，否则回退操作。

（5）手续费模型 。LP 的收益来源便是手续费，在超导中手续费模型十分简单，交易额的万五。用户用 x 币换 y 币，我们的交易费扣除是在 y 端，并且手续费重新注入流动池，继续提供流动性。LP 可随时提取本金和手续费收益。

直接将 y 投入流动池：如果考虑两步操作的原子性，即在用户兑换交易后，超导立即将 k*M 数量（手续费比例）的 y 币再投入到流动池中——仅在这种情况下可以由超导单方向存入。在假定用户兑换时是处于正常市场汇率情况下，超导直接投入 y 币有助于帮助场内汇率向正常市场汇率滑移。这个问题的本质是手续费收益不会被套利者搬走，我们知道兑换后出现了场内滑点，而滑点偏差正是套利者的套利空间，如果我们在兑换后直接将所有的 y 端手续费重新投入流动池，会更改 D 值，即曲线发生变更（如下图举例示意，一开始曲线是最下面那条且场内点处在最理性的平衡位置粉红色点，在一笔交易兑换后，场内点偏移到了红色空心点，此时直接将手续费回填，基于新的数量我们绘制出中间那条黑色曲线，而此时场内点的位置是紫色点，x 币数量没有改变，y 币数量增加了手续费数量），变更后的点（此时池中新的两种币数量表示的点）所在切线斜率会更偏近正常汇率点（绿色点）切线斜率，即这种手续费直接回填的操作像套利者一样在搬平场内已经出现的斜率（汇率）偏差，使得套利者基于中间曲线进行套利的空间变小。从下图中很明显直观看到套利者不再享受之前汇率明显偏差的红利，即对于最下面曲线用较少的 y（蓝色箭头）换得更多的 x 币（红色箭头） ，虽然依然可以套利，但成本要高于最初曲线的套利（图中箭头幅度）。所以这种手续费回填的做法，进一步压缩了套利者的套利空间，被压缩的部分利益转给了 LP 们，使得套利者和 LP 们共享之前那笔兑换中交易者多付出的滑点损失成本，而回填的手续费也依然全部归 LP 提取，套利者并不会分得。

假设我们开放了后续的单资产存操作，初始时 LP A 在提供流动性，投入了 5 个 x 币和 5 个 y 币，最下面曲线和粉红色点（D=10），随后交易者 X 发起一笔交易将场内点滑移到了红色空心圆位置，回填手续费（假设为 4.5 个 y 币）后曲线变更为中间曲线（D=19），点位置为紫色点，如果此时 LP A 全部提取资产，可以提 15 个 x 币和 5 个 y 币，比投入时要多出一部分利益，这部分利益空间就来自于该交易者 X 多付出的交易成本（滑点损失和手续费），但如果此时存在套利者从紫色位置搬移到绿色点，LP A 全部提取资产，可以提 9.5 个 x 币和 9.5 个 y 币，比紫色点可提取的 15 个 x 币和 5 个 y 币的总价值要少，原因是将交易者滑点损失成本的一部分分给了套利者，即便如此，LP A 依旧拿到了比自己原始本金（5 个 x 币和 5 个 y 币）加上手续费（5 个 y 币）更多的收益，原因就是手续费回填流动池压缩了套利者的套利空间，将交易者 X 的交易滑点成本一部分也分给了 LP A。

如果在滑移到紫色点时没有套利者出现，直接出现另一个 LP B 直接投入了 0.75 个 y 币，而不存入 x 币，则此时曲线直接变更为最外面那条曲线（D=20），此时场内点为灰色空心圆位置（15, 5.75）。根据下面的计息模型，LP B 和 LP A 分别占有的份额为：1/20，19/20。如果没有套利者在搬移，则 LP A 此时全部提取可以提 15*(19/20)=14.25 个 x 币和 5.75*(19/20)=5.4625 个 y 币，比紫色点时可提取（15 个 x 币和 5 个 y 币）要少一点，因为 LP B 分得了一部分来自交易者 X 滑点损失的利益空间，即 LP B 此时全部提取可以提 15*(1/20)=0.75 个 x 币和 5.75*(1/20)=0.2875 个 y 币，此时对于 LP B 来说可以提取到比存入资产（0.75 个 y 币）更多的资产，而利益空间就来自于之前交易者 X 多付出的交易成本，与手续费回填是一个逻辑。如果此时出现套利者进行套利，其可套得利益比之前从紫色点套到绿色点过程所攫取的利益更少了，原因是 LP B 也参与了交易者 X 交易成本的瓜分。但前提是 LP B 单资产存后不要反向超过平衡点，否则自己便又新造成了场内汇率偏差，需要承受被套利的空间。

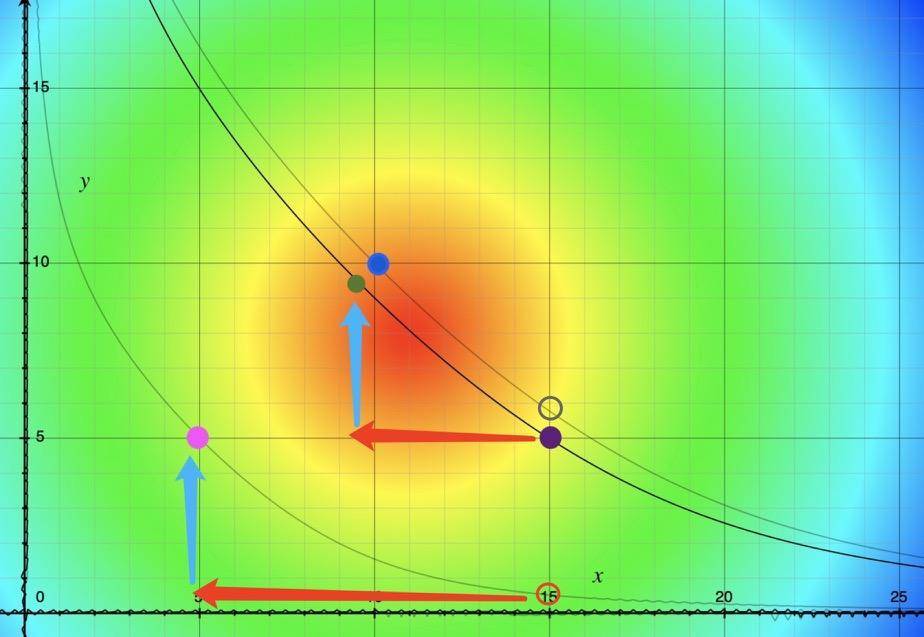
（6）年化计息模型以及提取 。MOV 超导记账规则（我们引入一种计息凭证，用于代表 LP 对池子贡献流动性的百分比）：

（1）如果没有流动性大小的任何变化，不论流动池中两种币的比例如何变化，甲的百分比不变，依然是自己持有的计息凭证数量除以当前总发行的计息凭证数量；

（2）当流动性大小改变后（add liquidity/withdraw liquidity/fee from swap），计算出新的 D 值 D1，然后此时总发行的计息凭证数量是之前的 D1/D0 倍，如果此时甲提取自己的资产，百分比为甲持有的计息凭证除以此时总发行的计息凭证的数量（重要注意：不论是新 LP 投入资产还是交易手续费回填流动性池，我们统一抽象为流动性大小改变，这是唯一影响份额计算的因素，但只有在新 LP 加入资产时才全局计算一次总的计息凭证发行量，包括给予该 LP 的新增发的计息凭证数量，上一个 LP 加入时刻到此时刻，这期间所有的手续费回填也都包含在了新总计息凭证数量计算过程中）。

举例：

T1：小明按理性比例存入 1 ETH、100 DAI，获得系统分发的 1 计息凭证，此时总计息凭证数量也为 1；

T2：在接下来一个月里，发生了许许多多交易，但并没有新 LP 加入，手续费让池子规模变为 2 ETH、200 DAI（在一个月中ETH行情平稳），注意此时虽然手续费改变了池子流动性大小，但并不需要在每一笔交易后去计算新的 D 值，也不需要根据新的 D 值倍数去增发计息凭证 —— 这一个月期间总计息凭证数量并未发生改变，而小明的份额也未发生改变，他依然拥有池子百分百的流动性提取份额

T3：小刚按理性比例存入 1 ETH、100 DAI，此时根据两种资产的数量计算新 D 值 D1，得 D1 = (3/2)D0（D0 为小刚加入前计算得的 D 值），因此得到新总计息凭证数量应该是之前的（3/2）倍，即此时系统总共有 1.5 个计息凭证，其中 1 个计息凭证是之前小明的，剩下的 0.5 个计息凭证是分发给新 LP 小刚的 —— 此时小明的份额将变成（2/3），可提取 2 ETH 和 200 DAI，而小刚的份额将变成（1/3），可提取 1 ETH 和 100 DAI。

注意：上面例子中小刚加入时的理性比例跟 T1 和 T2 时刻一样，实际上在 T2 期间，ETH 可能会涨涨跌跌，导致 T3 时刻场内资产数量比例发生变化，但并不影响我们的计算逻辑，小刚依然按照此时场内的数量比例投入资产，继续按照 T3 的计算过程完成计算即可。

这也是 MOV 超导给予 CFMM 完善发展贡献的一份力量。

滑点数据与保护

我们直接给出 MOV 超导滑点数值实验：

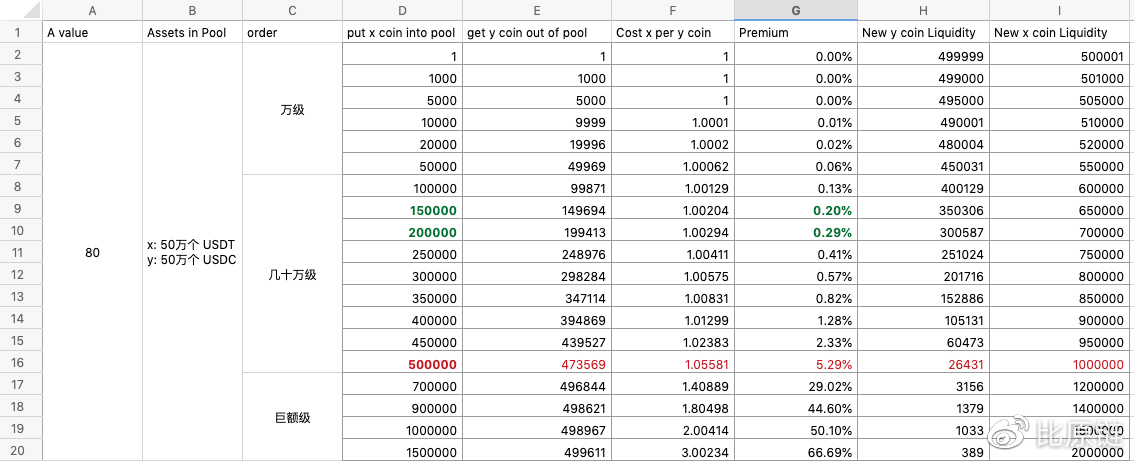
在 50 万量级流动性下，一次性大额交易 20 万美元的滑点为 0.29%（千三），相比于几大中心化交易所也具备充分的竞争力。我们会在 0.5%～10% 范围内设置滑点保护档位，给予一次性大额交易充分的滑点保护，避免给交易者带来过大损失，但这里要注意的是，滑点保护机制需要能够获取一种客观的市场汇率作为参照才能够发挥保护机制，而同时不妨碍套利者维持场内汇率恒定和反方向正常交易者正常交易秩序，我们称这种手段为【场参照系/统一场】，也是 MOV 超导在不断完善 CFMM 的地方。另外一档保护为，如果上链时发现与用户提交时汇率不同，可以允许有 0.05% 的偏差，超过则回退资产。

这里我们重点讲一下表格实验的由来，方便后来人借鉴参考。在我们的核心公式中，D 决定池子流动性规模，A 表示向直线偏移权重，A 的选择至关重要。D 随着流动性更迭在不断变化，而 A 一经选定，可稳定被采用。A 不可以太小，比如 1～50，否则在曲线中心范围内会存在明显的滑点，过早丧失交易吸引力；A 不可以过大，比如 > 200，否则会使得曲线价格发现失去根据市场汇率变动而调整的空间，同时给予极端套利者瞬间清空池中单方流动性的可能性，因为成本很低。如上图是流动性规模为 50 万量级，大概是在其三分之一处存在千三的滑点（包括万五手续费），当 A 保持不变时，不论流动性规模变更为多少量级，比如 30 万，也是在其三分之一处存在千三的滑点，即 10 万交易量。

深奥的数学问题

到此 MOV 超导实用性的篇章已经讲完。下面是一些非常有意思的 CFMM 数学问题，相信会随着 CFMM 的壮大，不断走向专业性，也会吸引更多学术界人士，开展更为先进的 CFMM 机制。

（1）牛顿迭代法 。

深入到工程细节，隐函数方程是很难直接根据 x 求出 y。因此我们借助著名的牛顿迭代法来实现兑换公式。

迭代法是利用逐次逼近过程求解非线性方程，同样的计算过程往往要多次进行，而每次都要以前一次计算结果带入计算。 一般100次运算完全能得出相当精度的结果。迭代法求解方程的过程是多样化的，比如二分逼近法求解，牛顿迭代法等，这里采用牛顿法。牛顿-拉弗森方法提出来的思路就是利用切线是曲线的线性逼近这个思想。

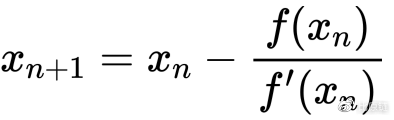
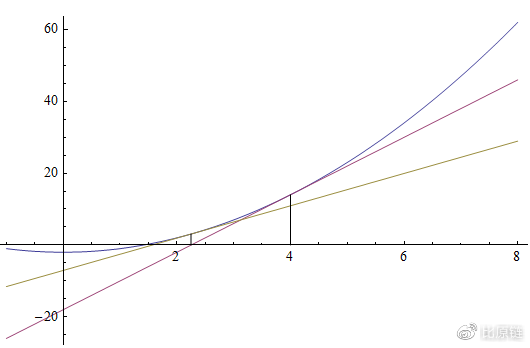
牛顿迭代法是一种很棒的迭代法。因为在它在大部分情况下都收敛，而且收敛速度很快，有效数字位数以指数级增长（证明可以通过洛必达或者泰勒展开）。

收敛的充分条件：若 f 二阶可导，那么在待求的零点 x 周围存在一个区域，只要起始点 x0 位于这个邻近区域内，那么牛顿-拉弗森方法必定收敛。也就是说，在这个区域内，用切线代替曲线这个直觉是合理的。但是，因为我们不知道根点到底在哪里，所以起始点 x0 选择就不一定在这个区域内，那么这个直觉就不可靠了。

我们将超导原始核心公式进行变形得如下形式：

Plain Texty^2 + y * (sum' - (A * n^n - 1) * D / (A * n^n)) = D ^ (n + 1) / (n ^ (2 * n) * prod' * A)

其中 y 就是我们现在正在求的 j 币的总数量，sum‘ 是将 j 币排除在外其他所有币种的总数量之和，prod’是将 j 币排除在外其他所有币种数量的乘积，n^n 表示 n 的 n 次方。

上面公式可以抽象为一元二次方程：

Plain Texty^2 + B * y = c

在代码实现中构建 B 和 c 的表达式，令 b = B + D。进一步按照牛顿迭代法，有

Plain Texty' = y - f(y)/f'(y)

其中

Plain Textf(y) = y^2 + B * y - c

化简即得代迭代公式：

Plain Texty' = (y * y + c) / (2 * y + b - D)

对该式进行循环迭代，直到最终精度缩小到某一范围内，即得到精确的 y 值。经过测试，收敛速度十分迅速。

同样除了兑换函数，每次流动性变化后核心公式中的 D 也要跟着池中的数量变化而变化，依然采用牛顿迭代法进行 D 的求解。构建出 D 的迭代公式如下：

GoD = (Ann*S + DP*xpLength) * D / ((Ann-1)*D + (xpLength+1)*DP)

（2）交易路径独立。

这个问题可以简化为，交易者将一笔大交易拆分成多个小交易依次进行交易和一次性完成大交易，哪一个更减少摩擦损失。

路径独立（path independent）假说：

交易一为 (∆, Λ)，交易二为 (∆′, Λ′) ，将二者合并为一个交易 (∆ + ∆′, Λ + Λ′) ，下面公式表示的意思是，我可以用 ∆ 数量的 i 币换取 Λ 数量的 j 币的前提下，当且仅当我输入 ∆ + ∆′ 数量的 i 币能够换取 Λ + Λ′ 数量的 j 币时，那我就可以在用 ∆ 数量的 i 币换取 Λ 数量的 j 币后，再用 ∆′ 数量的 i 币换取 Λ′ 数量的 j 币。反过来也是如此。

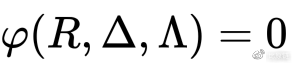
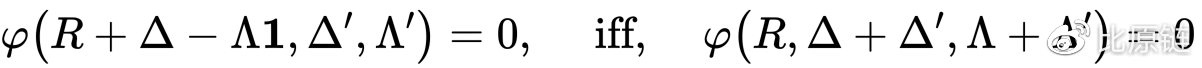
与此相对的是 path deficiency 假说：

当我输入 ∆ + ∆′ 数量的 i 币能够换取 Λ + Λ′ 数量的 j 币时，如果我更换策略，先执行用 ∆ 数量的 i 币换取 Λ 数量的 j 币的交易，然后再去换取 Λ′ 数量的 j 币时，会发现 ∆′ 数量已经不够用了，需要大于 ∆′ 数量，损失由此产生。

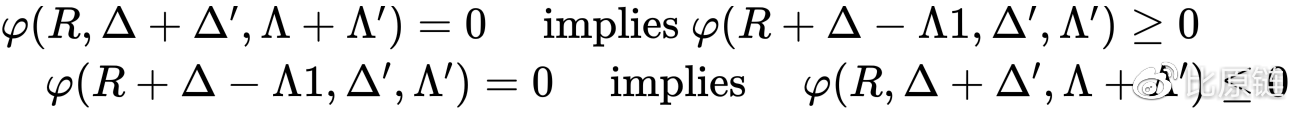
path deficiency 假说的意义是，对于交易者来说，将多笔交易聚合成一笔交易，比分开来交易，更划算。

本来 CFMM 属于路径独立型，但是，在引入手续费计算时，交易将从 path independent 变为 path deficiency【1】，证明过程我们借用论文【2】：

简单来讲，我们分别表示出合并成一笔交易可以换得的数量和拆分成两笔交易获得的数量之和，对二者进行比较。最主要的过程就是移项化简得到第三个式子，证得其恒为正。

（3）凸优化与套利策略。

这是最后一部分内容，与套利者套利策略和路径规划有关。首先来看一下高深的凸分析或者凸优化：

凸优化就是：1、在最小化（最大化）的要求下，2、目标函数是一个凸函数（凹函数），3、同时约束条件所形成的可行域集合是一个凸集。

依然费解。来看一个例子：

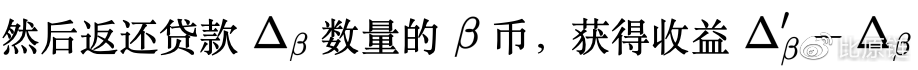
很简单的一个套利过程其实可以用凸分析来量化策略。我们有：

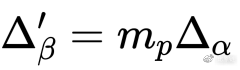
构建凸优化（这里用恒定乘积函数做示例）：

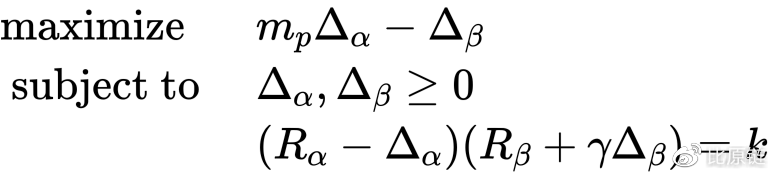
但这不够具有明显的凸性，进一步变换：

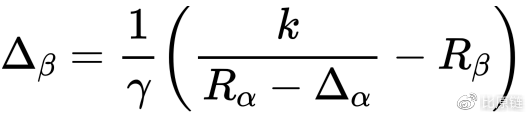
因此得到标准的凸分析形式：

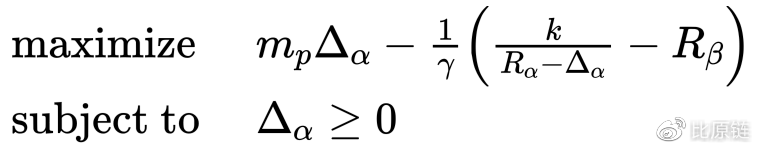
便可以借助专业的数学凸分析工具，自动完成计算。

上面展示的是一维的凸分析，优势不够明显，似乎直觉更有效，但在多维场景下，比如多种币的交易市场，对于套利者来说，就必须要清晰自己最优的套利策略，有点类似动态规划问题，十分困难，但这里便可以借助凸优化：

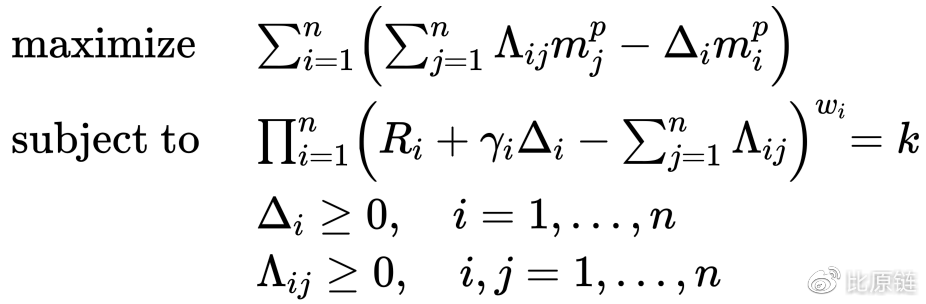
最后，超导不止于稳定币 CFMM！

引用文献

【1】Guillermo Angeris, Improved Price Oracles: Constant Function Market Makers, 2020, https://arxiv.org/pdf/2003.10001.pdf

【2】Uniswap, An analysis of Uniswap markets, 2019, https://arxiv.org/pdf/1911.03380.pdf

【3】Balancer, A non-custodial portfolio manager, liquidity provider, and price sensor, 2019, https://balancer.finance/whitepaper/

【4】Robin Hanson, Logarithmic Market Scoring Rules for Modular Combinatorial Information Aggregation, 2002, http://mason.gmu.edu/~rhanson/mktscore.pdf