Defi流动性挖矿大热,参与Balancer前你应该知道这些概念


写在前面:
随着近期Compound治理代币COMP的大热,Defi“流动性挖矿”潮正式来临,而同样备受市场期待,又有着高级版uniswap之称的 Balancer ,也即将迎来自己的治理代币挖矿。而在参与Balancer的流动性挖矿之前,你需要对几个概念有所了解,一是如何计算Balancer储备池的值,二是计算无常损失,最后则是关于滑点的计算,对于这些,Balancer首席执行官Fernando Martinelli将为我们一一道来。

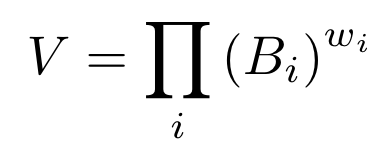
Balancer储备池的值
一个Balancer储备池,可以由多达8种不同的ERC20代币组成,并且每种代币都有自己任意的权重。这个权重表示储备池在任何时候,应在每个代币中保持的值的百分比。只要市场上有活跃的理性套利者,且池的费用很低,则储备池持有的每个代币的价值百分比,预计总是非常接近池的权重。 (关于高收费Balancer池的情况,请看这篇 文章 )
在低费用的情况下,只要任何一个代币相对于另一个代币有价格变化,套利者就会受到激励,以使代币之间的资产池价值分配,恢复到原始预定义权重。
为每个代币灵活选择权重的有趣效果是,储备池流动性提供者(LP),可以控制他们希望对每种资产承担的风险水平。例如,如果他们看好MKR(相对于ETH),他们可以选择向MKR权重高、ETH权重低的储备池中添加流动性。如果不存在这样的储备池,他们也可以自己创建一个。这样,当MKR相对于ETH上升时,他们将获得MKR的大部分上行空间。
当然,这一优势并不等同于持有100%的MKR,但它将比在MKR和ETH之间拥有50/50的储备池要好得多。下面的截图,显示了在实践中的情况。
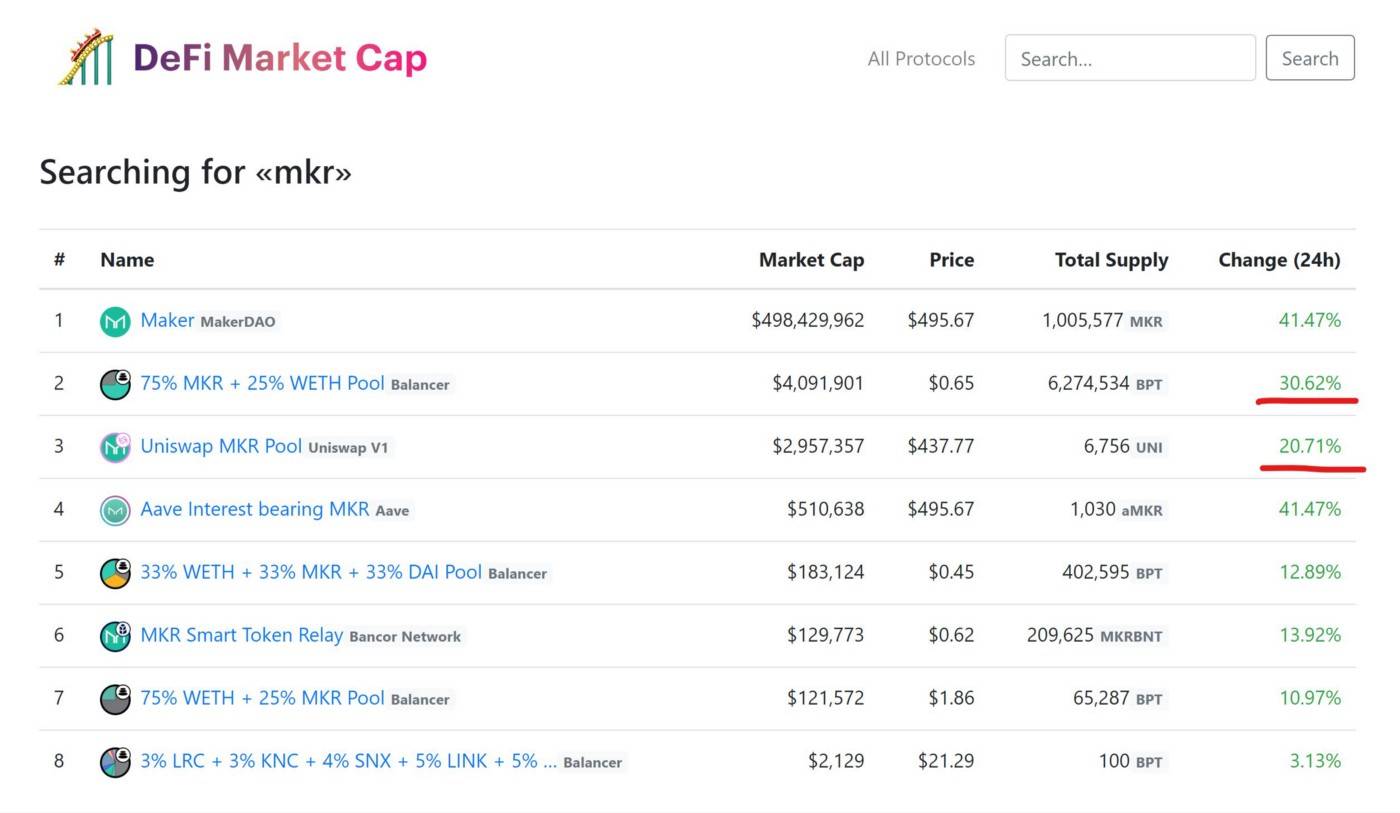
在向Balancer储备池提供流动性时,你可能会问的一些关键问题是:
- 在基础代币的价格全部改变之后,是否有一种方法可以概括计算出Balancer储备池的值?
- 如果MKR的价格翻倍,且ETH保持不变,那么持有75%MKR和25%ETH(类似于上面的截图)的储备池的价值将增加多少?
- 如果权重为10%的代币价格下跌80%,那么储备池损失是多少?
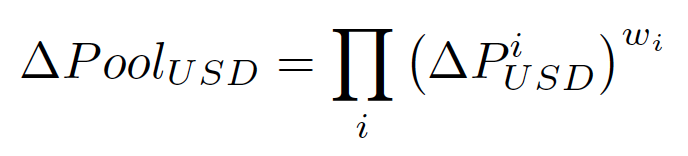
这个方程的长形式证明,可以在我们网站上的 详细文章 中找到。
有了这个公式,我们就可以轻松回答上面提到的问题,请注意,无论代币的权重如何,不变的代币价格都不会影响储备池的值(
ΔP_usd^w = 1^w = 1
),无论这些代币的权重如何。所以我们有:
- 如果MKR的代币价格翻番,75%MKR和25%ETH的储备池的总价值将增加68.2%(=2^0.75=1.682),而一个50/50比例储备池的总价值则增加41.4%(=2^0.5=1.414) 。
- 如果一个储备池中某个代币的权重为10%,且其价格崩盘80%(或ΔP_usd = 0.2),那么这个储备池的总价值只会下降约15%(=0.2^0.1=0.8513) 。
流动性提供者的无常损失(IL)
“无常损失”一词在Pintail的文章推出后被广泛传播。如果你之前从未听过这个词,可以阅读下Pintail写的关于Uniswap储备池回报的 重要文章 。
根据定义,无常损失(IL)描述的是这样一种损失:在储备池中的资产,较这些资产在池外的情况下损失的百分比,用公式来表达便是:
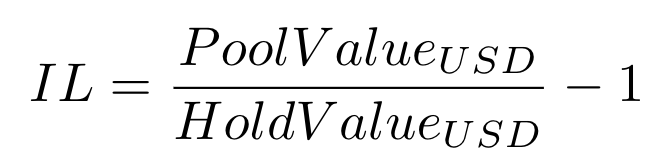
在等式中加上费用,流动性提供者(LP)的最终美元收益将是累计费用(以总储备池值的百分比计),减去无常损失。
我们可以使用以下定义来更改池中持有价值的变化,来扩展上述无常损失的公式:
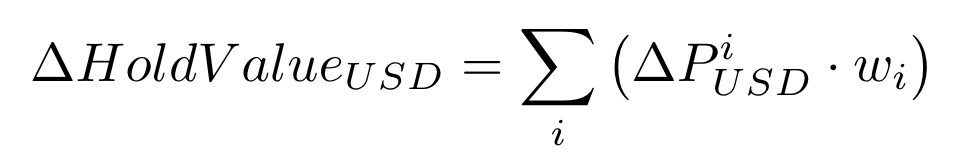
为了说明这个公式,我们举个例子,例如,假设一个篮子投资组合中,有一个权重为50%的代币,而它的价格翻了一番。那么这个篮子投资组合的总价值将增加50%,或1.5倍(=1*50%+2*50%=1.5)。换言之,假设我最初持有500美元的代币A和500美元的代币B,两者总共1000美元。如果代币B的价值翻倍,那么我就持有了500美元的代币A和1000美元的代币B,总计1500美元(即总价值增加了50%)。
如上面所述,无常损失也可以用储备池值和持有池的变化来表示:
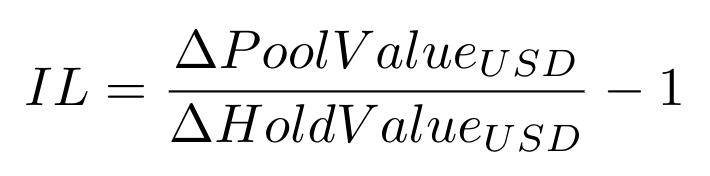
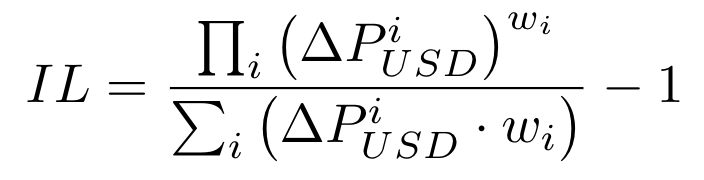
Balancer储备池的滑点
根据定义,滑点是指交易中,实际支付价格相对于现货即期价格的百分比变化。
在存在费用的Balancer储备池中,即期价格的定义如下(请注意,从这里开始,i是指输入代币,即交易者发送/出售给储备池的代币):
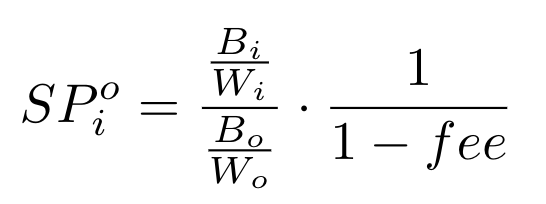
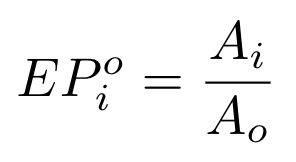
amountOut
公式,我们可以将其重写为:
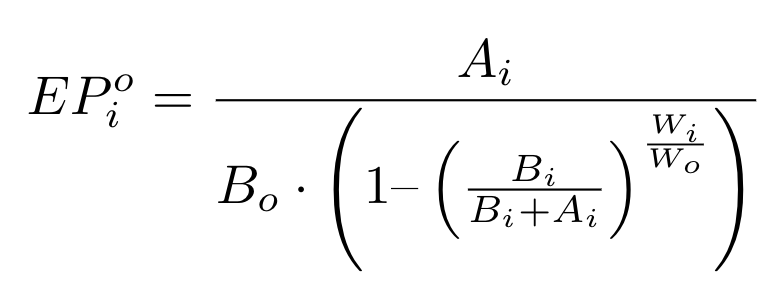
我们可以将滑点定义为有效价格超过即期价格的百分比。这是关于交易金额(Ai)的一个函数,因为它会影响有效价格:
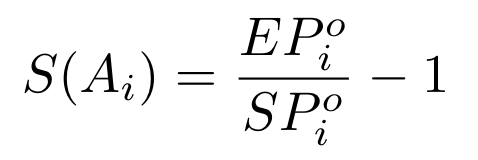
在Balancer中,滑点并不是线性的:它随着交易量的增加而增长得更快 。不过,作为一个近似值,我们可以线性化小额交易的滑点。下图以蓝色显示了增加数量的有效价格,以橙色表示的是有效价格的线性化(所有数字都是虚拟的):
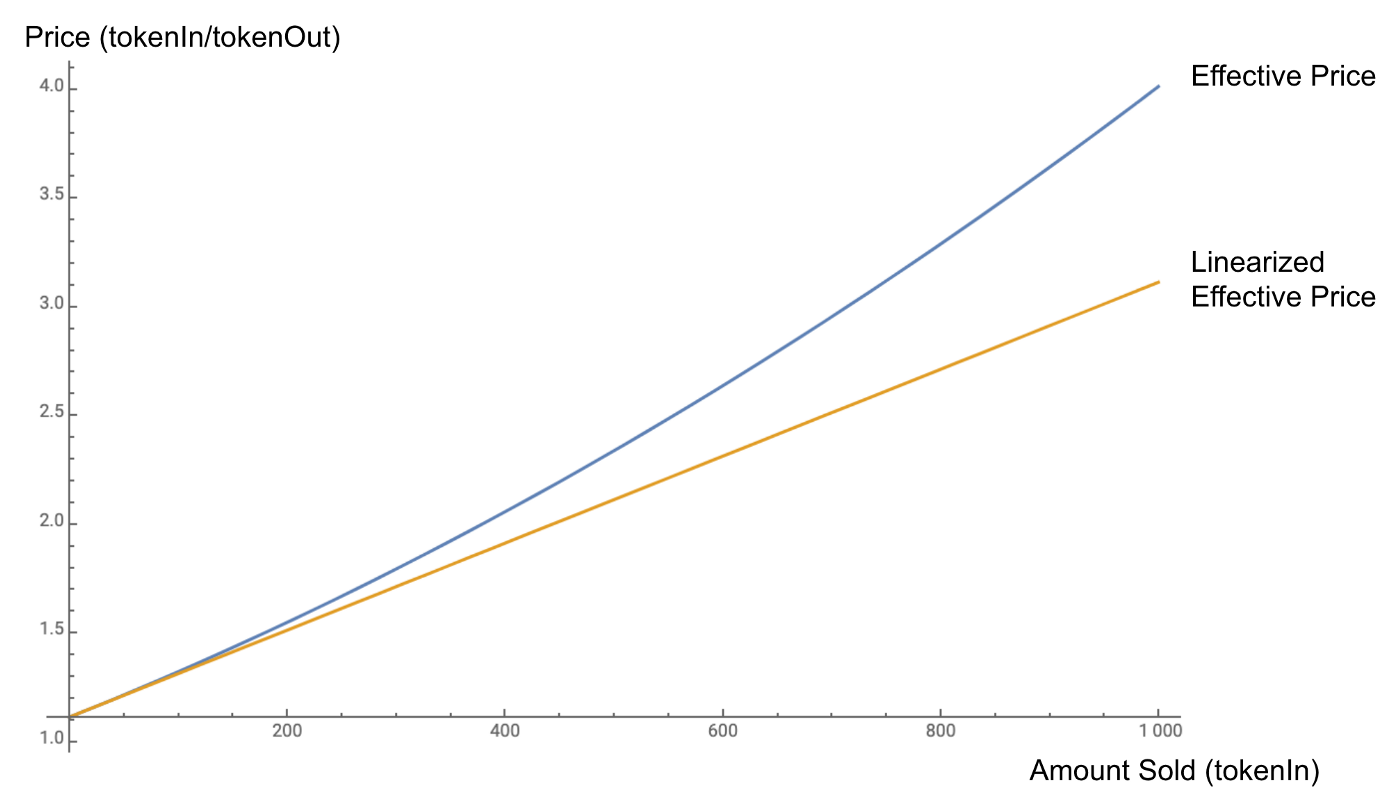
这种线性化对于许多算法优化(包括我们的智能顺序router (SOR))非常有用。
通过线性化,我们可以将滑点重写为交易金额的线性函数:
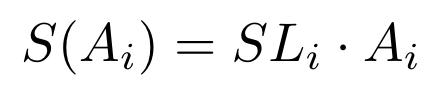
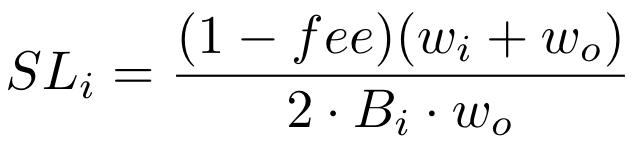
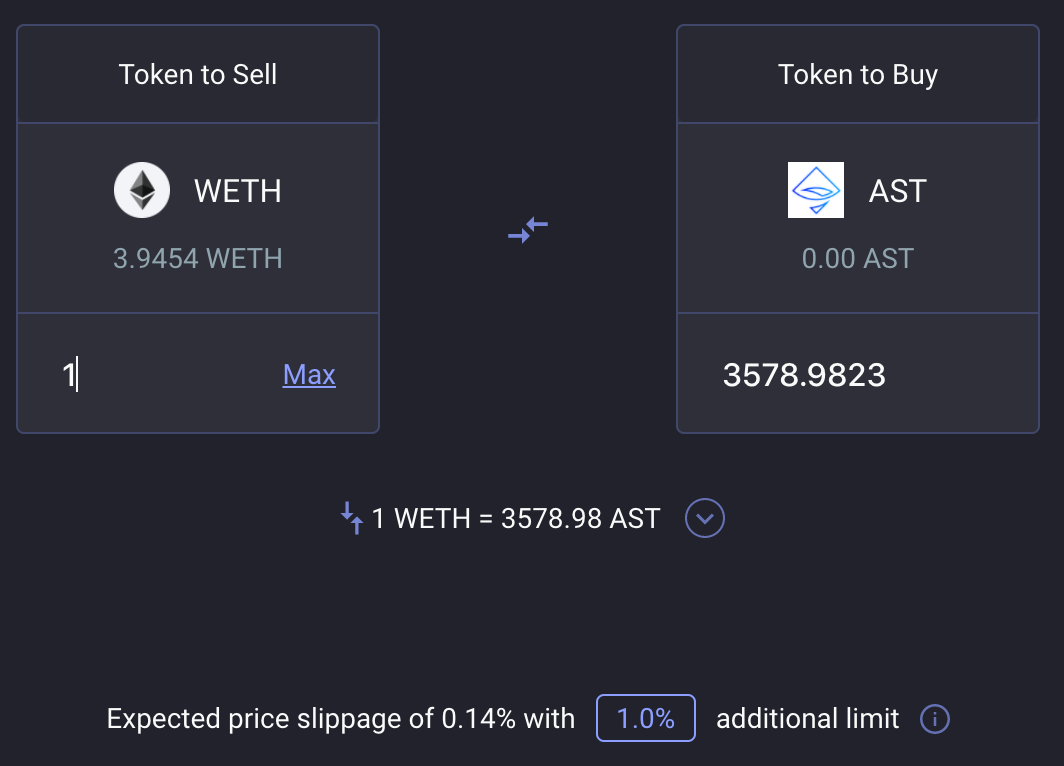
滑点计算实例
以一个70% AST / 30% WETH 的储备池为例。在撰写本文时,该储备池有414.7万AST和491 WETH:
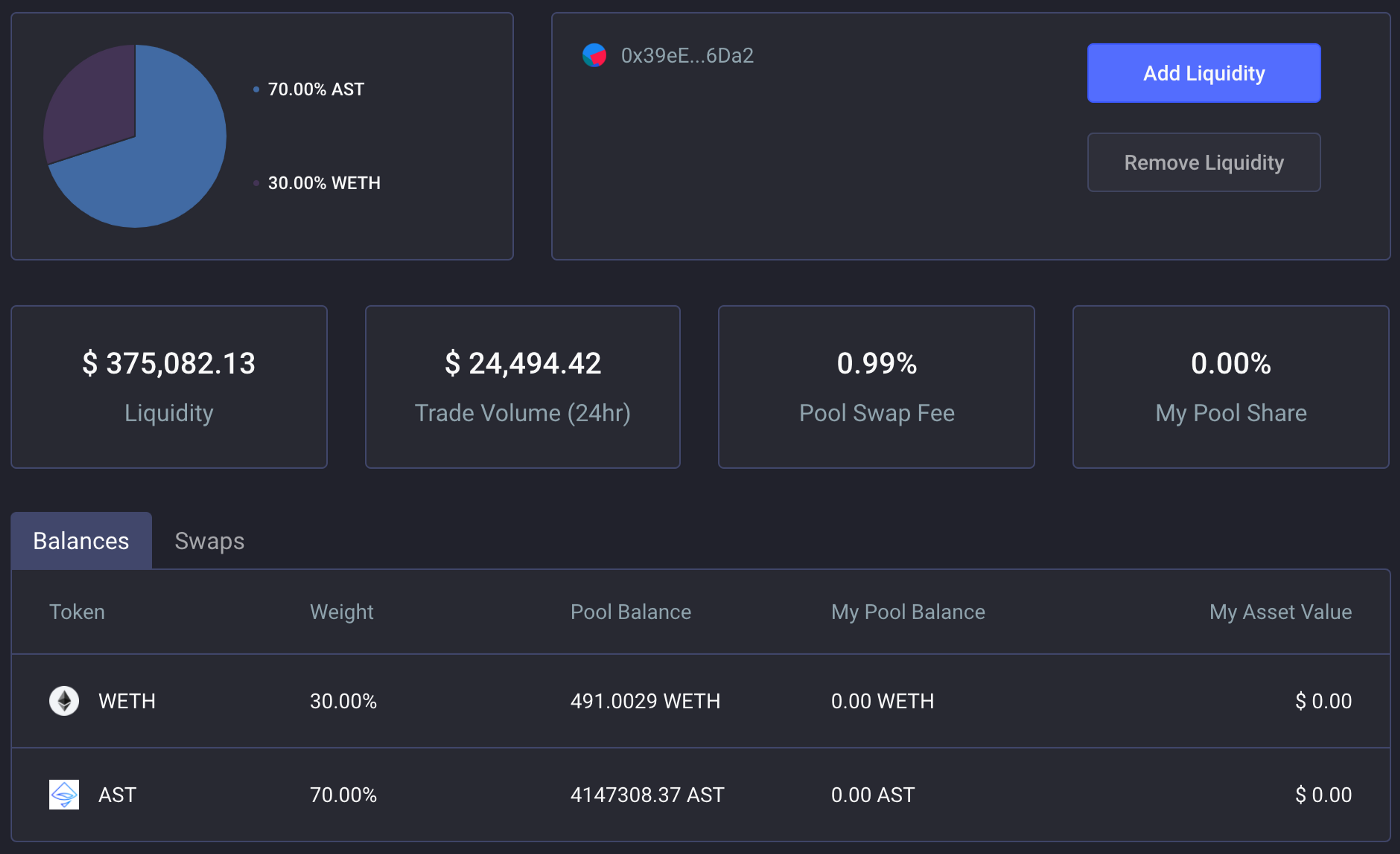
Bi
是出售给储备池的代币余额(491 WETH),
Wi
是出售给储备的代币权重(0.3),
wo
是从池中购买代币的权重(0.7)。所以这个储备池的线性滑点公式是:
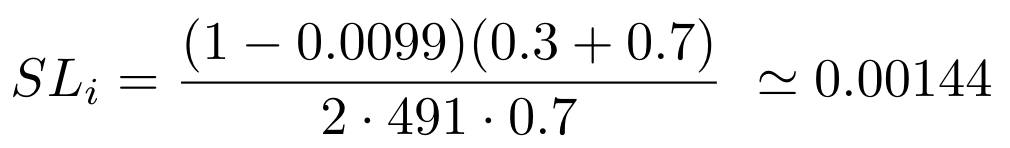
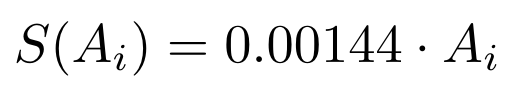
为了完整性起见,让我们推导出购买一种代币时,即
amountOut
(Ao)的滑点公式。公式非常相似,我们从相同的有效价格公式开始:
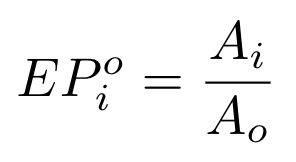
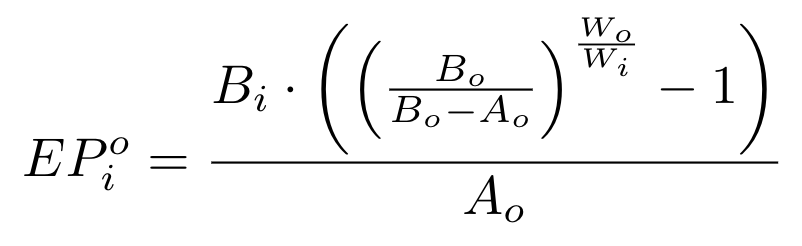
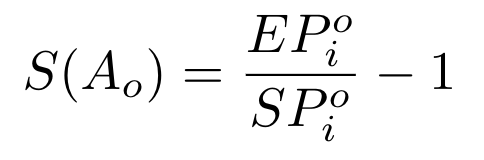
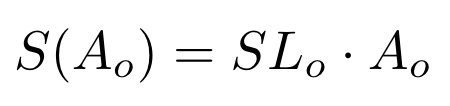
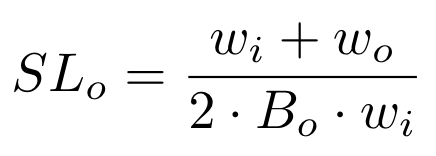
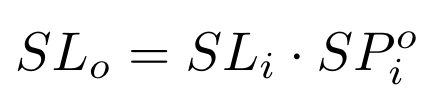
原文:https://medium.com/balancer-protocol/calculating-value-impermanent-loss-and-slippage-for-balancer-pools-4371a21f1a86 作者:Fernando Martinelli 翻译:洒脱喜 稿源(译):巴比特资讯(http://www.8btc.com/article/612146)




