正文

技术指南丨DE/CP场景下的分布式系统理论

华数云计算2020-05-29 11:10:58

DCEP与现有的电子支付系统有一个最大的不同点在于，DCEP整体系统的设计是 一个分布式的系统，整个支付流程需要多个系统与用户的终端协同完成工作 。而现有的电子支付，例如微信支付宝等产品，则是只采用了一个支付中心，用户的设备 仅仅是作为一个收集信息的终端 。

DCEP所具有的货币流通属性，其流通过程的细节，以及对离线支付的要求，需要系统以分布式的形式运行。

因此，作为一个分布式系统，DCEP的设计势必会受到一些分布式系统的基本逻辑与理论的影响。同时，DCEP的设计也会反映出这些逻辑与理论。

CAP理论

CAP理论是原本来自分布式数据库中的一个理论，这个理论描述了一个分布式系统设计中的取舍依据。

CAP是分布式系统中 一致性（Consistency），可用性（Availability）与分区容错性（Partition tolerance） 三个单词的简写。

这个理论的基本描述是， 分布式系统中三者最多只能实现两点，不能同时兼顾 。实际上这样的三选其二的理论有很多，不仅仅是在分布式系统领域有体现。

这三者分别具体地表达了如下的含义：

一致性：指的是分布式系统中所有节点被写入数据后，能立即的在任何一个其他的节点中能够读取到写入的值。
可用性：指的是整个系统能够一直正常的进行操作，来自客户端的请求可以一直得到系统的正常响应。
分区容错性：指的是其中部分节点离线，或网络出现故障的情况下，系统仍然能够正常使用。

实际上，分布式系统的设计逻辑，阐述的是分布式系统的三个属性中，只能有两个是强限制的，而另外一个是弱限制的即可。

CAP理论中三元素可以两两组合,形成三种组合方式：

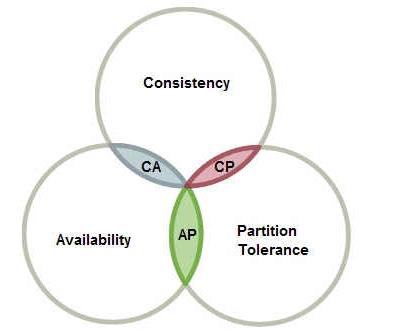
优先保证一致性与可用性，放弃分区容错性：实际上不存在这样设计的系统。因为一旦系统放弃了分区容错性，那就意味着这个系统不再是一个分布式系统的构建方式。
优先保证一致性与分区容错性，采用弱可用性：所谓的优先一致性与分区容错性，就是设计系统能够保证所有系统的一致，即便这种一致性在有节点离线的情况下也能保证。实际上系统会不断的重复在系统的组成节点上进行数据同步，并且是强一致的同步。这就导致了系统中某一个节点存在写入行为时，其他的节点不能够写入，只有数据同步后才可以完成。实际上大多数区块链系统，尤其是经典的比特币系统就是这样的设计。在区块链系统的一个区块周期中，只有一个节点可以向网络中写入数据，其他节点的写入都需要等待下一个区块时间。
优先保证可用性与分区容错性，采用弱一致性：这种情况下，系统往往会牺牲一定的一致性来保证整个系统可以一直接收来自外部的写入请求。但是牺牲一致性不是不保证一致性，而是整个系统会随着时间的推进，逐渐的达成一致的要求。

根据DCEP的设计逻辑，在一次的具体交易流程中，参与交易的双方终端与数字货币登记系统构成了一个分布式系统。其中设备终端与登记系统都是这个系统中的节点。由于DCEP要求能够进行离线交易，也就意味着在一次交易中，即便有节点完全无法在线，最终在网络回复之后系统依旧能对交易的过程进行验证，保证交易的正确性。

从这个角度来看，DCEP的设计是 一种优先保证AP的设计 。

但是这样的设计会导致一个问题，那就是DCEP一定程度上放弃了一致性，会使得进行货币交易的时候有一定的双花风险。DCEP通过双重手段来降低与解决这种风险。

首先，DCEP的设计将系统出现不一致性的 可能性不断降低 ，保证非恶意情况下不会出现交易不一致的问题，同时能够一定程度上抵御恶意的双花。

同时，DCEP通过技术之外的手段保证了一旦发生恶意双花情况，可以对进行违规操作的人进行 追责与管理 。

从这个角度上来说，DCEP的核心设计逻辑中，优先保障系统的可用性与系统的分区容错性，在满足这个前提的情况下尽量的提升系统的一致性。