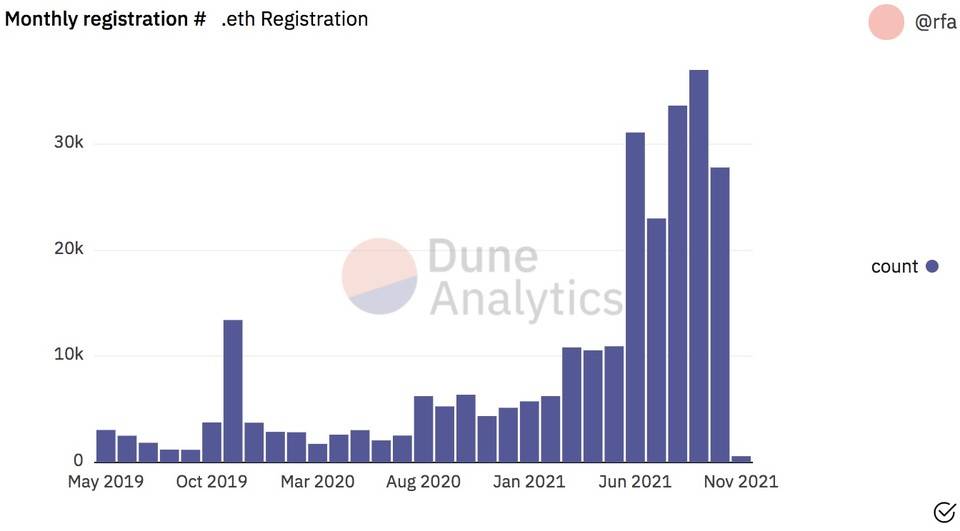
说透热门的常数函数做市商:这是 DeFi「从 0 到 1 」的创新


编译:Perry Wang
在很多市场中,如果缺乏足够的 有机流动性 来支持活跃交易, 做市商 就成了缓解问题的代理人,它们可以促成原本不会发生的交易。
自动化做市商 (AMM) 是执行这一功能的算法代理人,在电子市场内提供流动性。
尽管有很多人在理论和实践上研究过自动化做市商,但「 常数函数做市商 」 (constant function market makers,简称 CFMM) 在学术领域和金融市场上,都是一个 从 0 到 1 的创新 。
链闻注:
-
在数学中,常数函数(也称常值函数)是指值不发生改变(即是常数)的函数; -
《从 0 到 1》是由硅谷知名投资人 Peter Thiel 课堂笔记集结而成的书,曾经是创业者炙手可热、人手一本的「创业圣经」。
在本文中我将:
-
解释 AMM 和 CFMM 之间的 差异 -
探索 CFMM 的 利弊 ,探讨 CFMM 未来的 设计方向及用例
尽管加密社区对自动化做市商 AMM 颇为兴奋,但大家对相关术语有很多 误解 。
当人们提到 AMM 时,大多会想到 Uniswap ,但 AMM 这个概念在学术界已有 10 年 的深入研究,研究主要集中在信息汇总的设计,以及如何应用于某些市场,在这些市场,回报依赖于世界的某些未来状况,例如预测市场。
人气最高的 AMM 是「 对数市场评价法则」 ( Logarithmic Market Scoring Rule,LMSR) ,该法则于 2002 年提出,被用于大多数 预测市场 (例如 Augur V1 和 Gnosis) 。AMM 的信息汇总还有其他策略,例如贝叶斯做市商 (在二元市场表现不俗) 和动态同注分彩做市商 ( dynamic pari-mutuel market makers)(常用于赛马) 。
Uniswap 确实是一种 AMM,但它有更多限定条件。因为 Uniswap 做市商使用了一种 恒定乘积做市商 (下面将会深入讨论) , 我们可以把这一类 AMM 称为「常数函数做市商」,即 CFMM。
当谈到 CFMM 时,我们还经常听到「 联合曲线 」 (bonding curve) 这一术语,实际上这是一个错误用法。联合曲线定义的是价格与代币供应量之间的关系,而 CFMM 定义的是两种或更多代币之间的关系。其实,该术语的创造者声称,联合曲线实际上希望用于「联合在一起的类宗教社区」的语境中。
最后,经常有人把像 Compound 这样的 算法贷款协议 称为 AMM。我认为,这些算法市场采用了某种类型的 AMM,而不是一种 CFMM,因为其 利率函数 会根据使用率而动态变化,其目标也不是要保持利率不变。
常数函数做市商 CFMM 究竟是什么?
CFMM 是专门用于真实金融市场的 第一批 AMM 。加密社区设计出 CFMM,来构建去中心化的数字资产交易所,它建立在一种函数之上,即依据两个或多个资产的可用数量来建立一种预先定义的价格组合。与基于订单簿的传统交易所不同,交易者是与一个 资产池、 而不是与某个特定的对手方交易。
「 常数函数 」 (constant function) 这一术语是说,如果某个交易会改变某些资产的储备量,那么这些 储备量 运算后的结果应保持不变,比如等于一个常数)。
CFMMs 通常有三个参与方:
-
交易者 :用一种资产交换另一种资产。 -
流动性提供者 (LP) :愿意将自己的资产组合与他人进行交易,获得一定费用 -
套利者 :让该资产组合中的资产的价格保持与市场价格一致,以赚取一定利润 -
CFMM 常用于 二级市场交易 ,其目标是精确反映某个具体资产在 参考市场 的价格 (也即套利的结果) 。例如,如果 CFMM 价格低于参考市场的价格,那么套利者会在 CFMM 买入这一资产,然后在一个基于订单簿的交易所卖出,从而获利。
由 Uniswap 率先实施的 恒定乘积做市商 策略,满足如下等式:
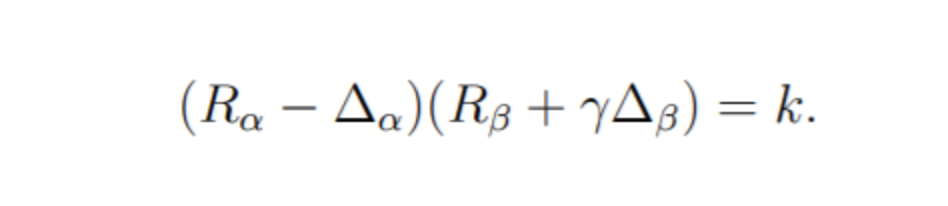
R(α) 和 R(β) 分别是某种资产的储备量,γ 是交易费。交易任何数量的某种资产,当改变其储备量时,必须保证:当交易费为 0,乘积 R(α)*R(β) 一直要等于常数 k。这常被简化为 x*y=k, x 和 y 分别是两种资产的储备量。在实践中,由于 Uniswap 收取 0.3% 的交易费,并将其投入储备,所以每笔交易之后 k 会增大。
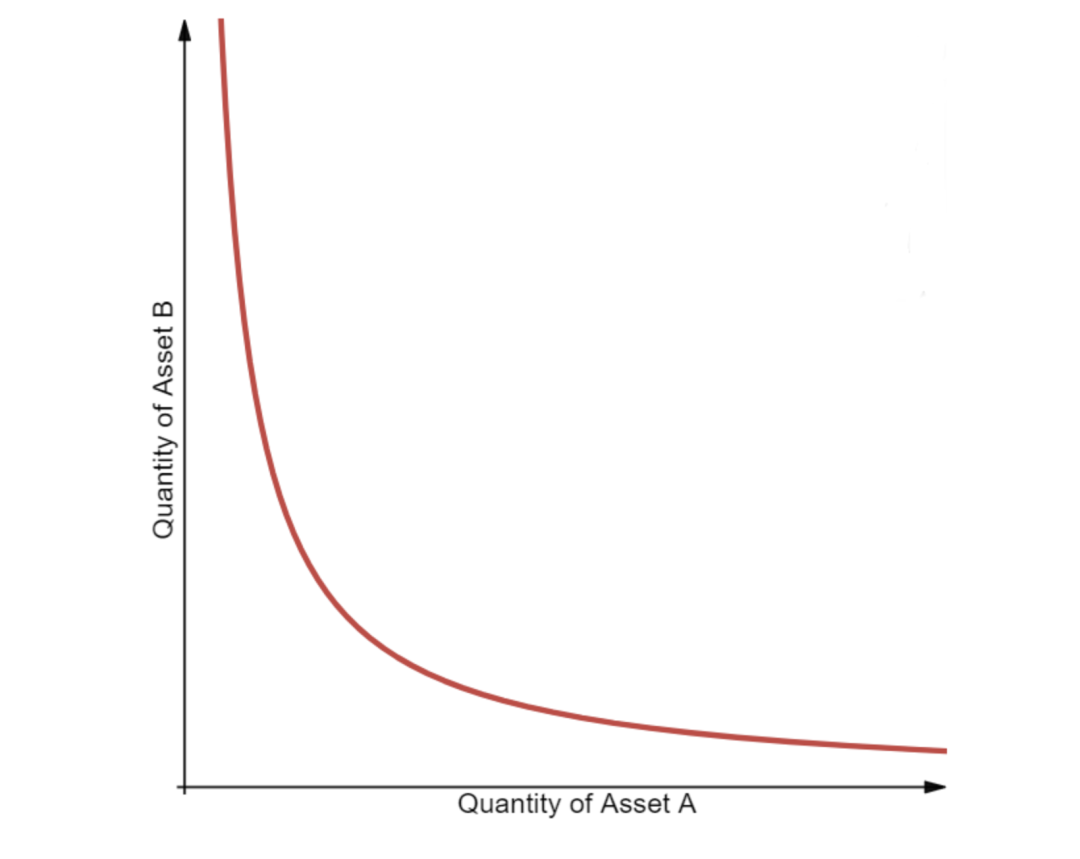
一个恒定乘积函数在描绘两种资产时会形成一条 双曲线 ,其特性让人比较满意,因为当价格趋近无限时 (在频谱的两端) ,流动性都不会匮乏。
恒定总和做市商 (Constant Sum Market Makers)
恒定总和做市商,是 CFMM 一种相对直接的应用,满足如下等式:
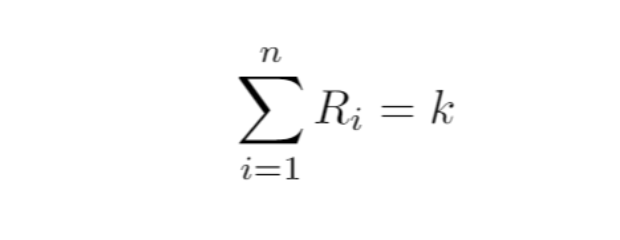
R(i) 是各资产的储备量,而 k 是一个恒定值。尽管这个函数产生「 零滑点 」,但它不会提供无限流动性 ,因此不适于在去中心化交易所的用例中单独实施。在实践中,如果某储备代币的 参考相对价格 不为 1 时,总会出现套利者吸干这种代币的情况。
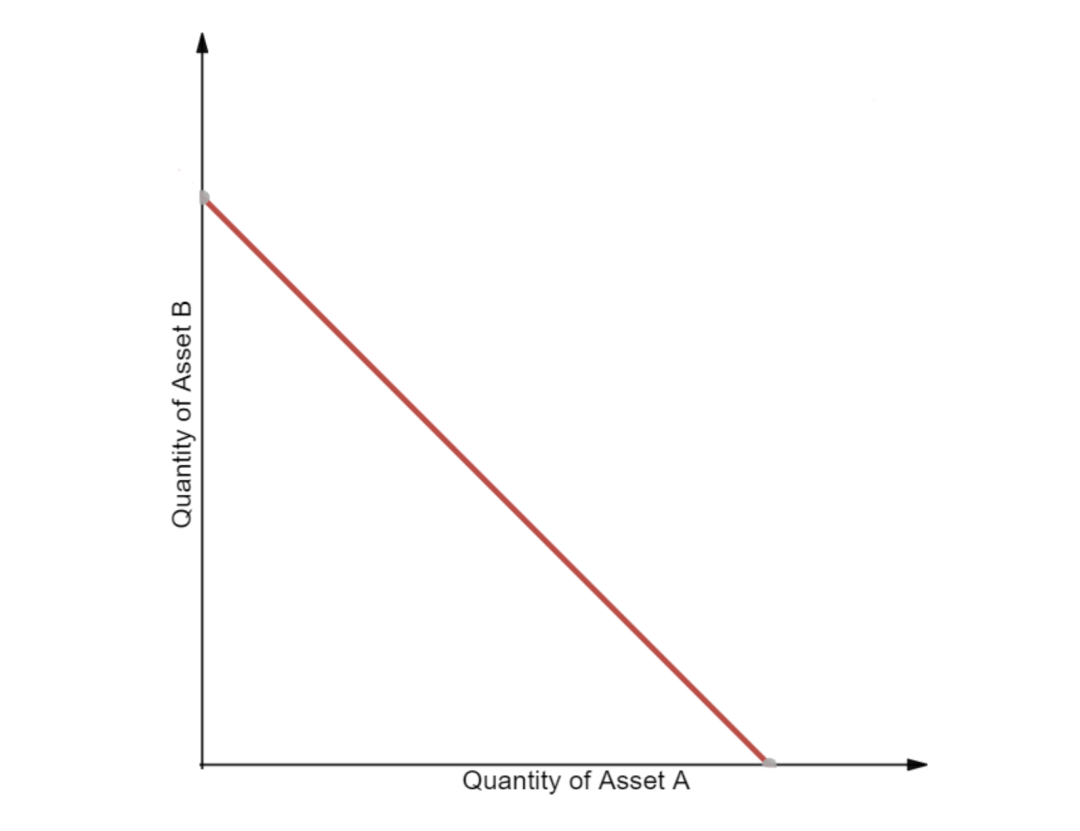
当描绘两种资产价格时,恒定总和函数会形成一条直线,结果就是等式 x+y=k 。
恒定平均值做市商 (Constant Mean Market Makers)
恒定平均值做市商 ,是恒定乘积做市商的一种概括,可用于超过两种资产的情况,权重可不限于 50/50 。 Balancer 率先引入这一模式,在无交易费的情况下,恒定平均值市场满足如下方程式:
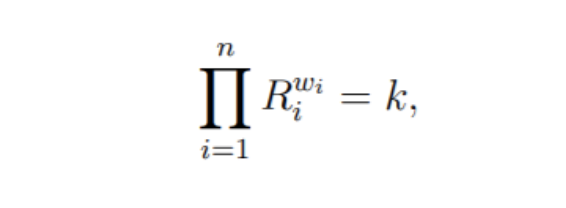
R 是每种资产的储备量, W 是每种资产的权重 , k 是常数。换句话说,在无费用时,恒定平均值市场确保了 资产储备量 的加权几何平均值保持不变。
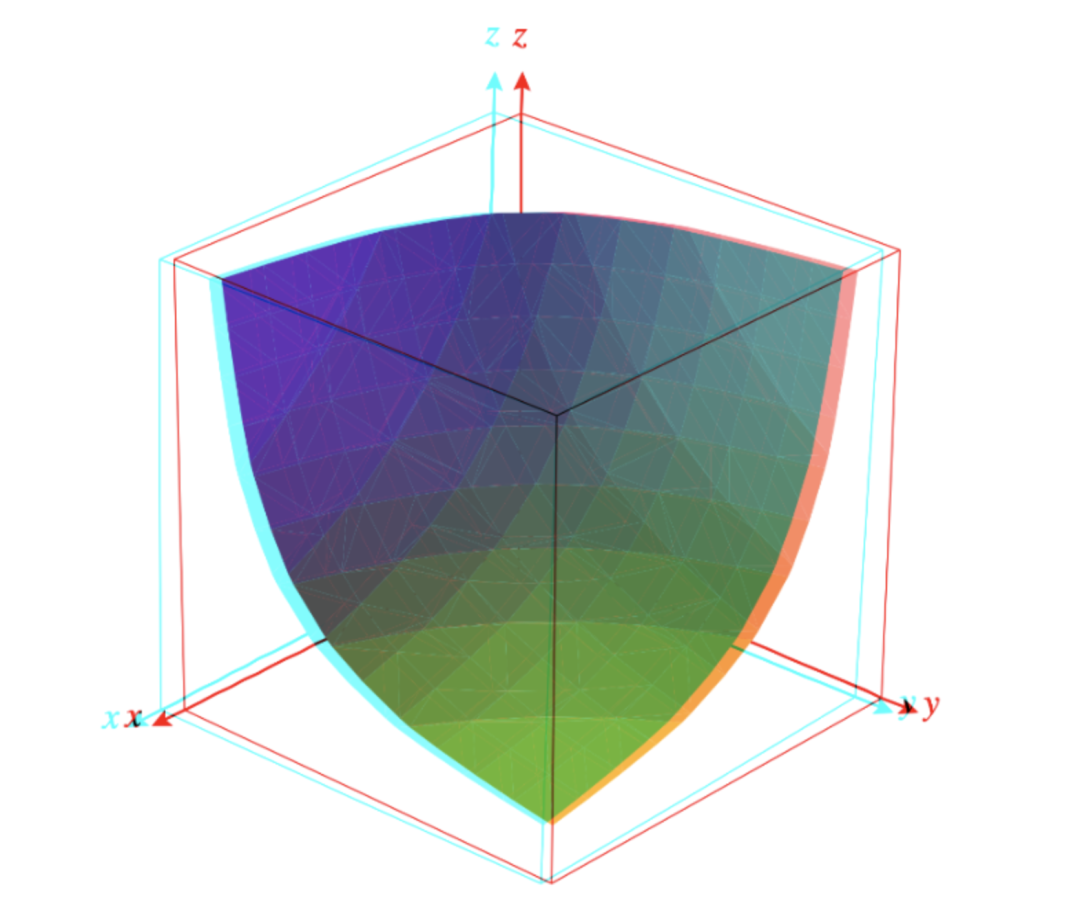
譬如,三种资产等权重组合资产的函数为:(x*y*z)^(1/3) = k
混合型 CFMM
有一些项目采取的是 混合函数 ,基于所交易资产的特性而实现想要达到的目标。
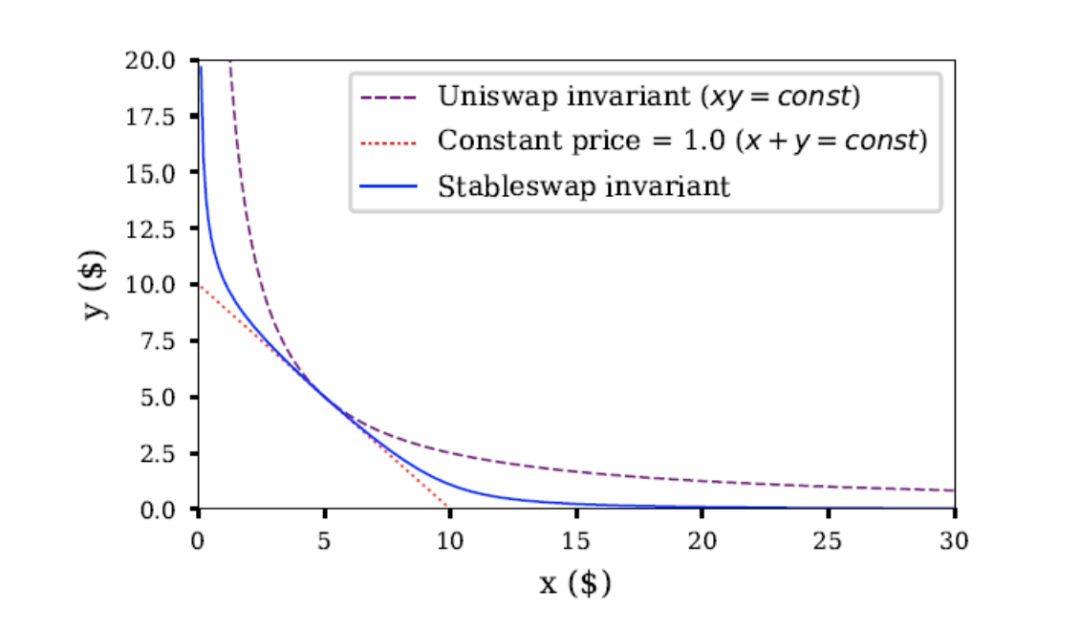
Curve (又名 Stableswap) 发现,如果基础资产的价格相对稳定 (例如,两种以美元计价的稳定币) ,那么你可以降低函数中的滑点值。它使用了一个恒定总和函数与恒定乘积函数的 混合体 ,得出以下这个相当复杂的函数:
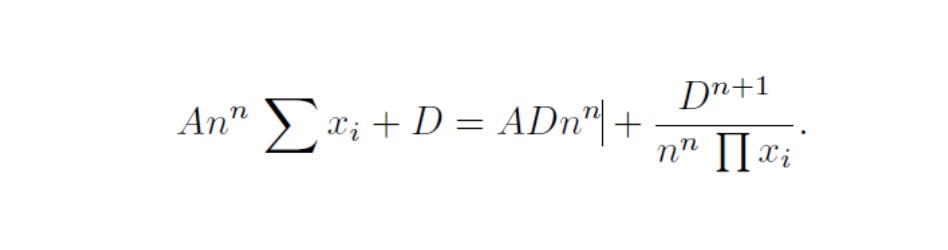
x 是每种资产的储备量, n 是资产的种类, D 是一个不变量,代表储备中的价值,A 是「放大系数」,即一个可调的常数,提供一种类似杠杆的作用,影响资产价格的范围,后者会影响流动性提供者的利润空间 (即资产的波动性越高,A 也越大) 。
当投资组合比较均衡时,这个函数作为一个恒定总和函数而发挥作用,当投资组合变得更不均衡时,它转换为一个恒定乘积函数。在效果上,这个函数看起来像一个「 放大的双曲线 」。
Shell Protocol 的目标类似,但采取了一种不同的方法。和 Curve 一样,其滑点已针对稳定币进行了优化,和 Balancer 一样,其代币资金池是一篮子的加权资产,但是与上述两者的区别在于,它使用了 多个可调参数 。它使用的函数如下:
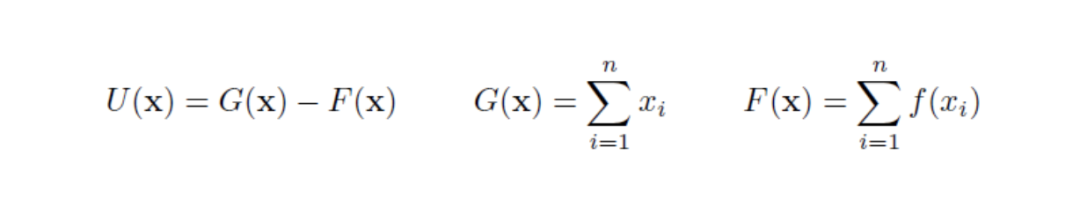
U(x) 可被诠释为由一个增益函数 G(x) 和一个损失函数 F(x) 组成的 效用函数 ;x 是每种资产的储备量。在效果上,当资金池处于平衡时,该函数相当于一个恒定总和函数,但当资金池各资产的权重偏离某个特定的阈值时,它会逐渐引入更多的滑点。这种设计可确保资金池保持均衡,靠拢它对各资产所预设的权重。
常数函数做市商的好处
交易更快
在传统交易所的工作流中, 做市商 需要创建订单,订单要在交易所中挂出,做市商需要浏览订单,再等待有交易对手接单。受制于这种匹配流程,某些订单可能得等上好一段时间才会被接单,或者一直等待。而 CFMM 解决了经济学上的「 需求耦合 」 (coincidence of wants) 问题,让一笔交易可以 立即发生 ,对于某些用例而言这非常重要 (例如因流动性过低而难以做市的游戏内的物品) 。
引导流动性
在基于订单簿的交易所, 引导流动性 是一个特别费力、成本极高的过程。通常情况下,交易所需要找到做市商,让他们编写用于定价和发布订单的客制代码,并经常直接提供帐户和资金,以便于交易。交易所往往还要运行带有控件的内部交易台,以确保既不抢先交易,还能靠自己应付一些执行工作。要么,创始人还要经常倒腾一段 python 脚本 ,用自己的资产提供流动性,同时对冲他们在其他交易所的风险。「 德尔塔中性 」 (Delta neutral) 型做市商如果想找到一种对冲其资产偏离账面的方法,任务也比较艰巨,因为如果不存在某个自然人的买方或卖方,这通常是不可能实现的。
由于 CFMM 鼓励被动的市场参与者将其资产借给资金池,因此它们使流动性的提供的便利度有数量级的提升。例如, Synthetix 能够用 Uniswap 来为其 sETH 流动性池引导流动性,让用户可以更方便的在交易所开始交易。
链上预言机
CFMM 提供了一种能力,即无需使用中心化的第三方即可衡量某个资产的价格,从而解决了所谓的「 预言机问题 」。与 CFMM 互动的代理 (agents) 会因为正确报告某个资产的价格而 获得激励 ,因此,去中心化交易所变成了一个良好的链上价格预言机,其他智能合约可以将之作为一个真实信息的来源。
Uniswap v2 可以在每个区块的首笔交易之前度量和记录价格,这就更加落实了初衷。与此前在一个区块期间寻找价格相比,这样使得价格更难被操纵。
路径独立性
路径依赖的意思,简而言之就是「 历史很重要 」。基于订单簿的交易所,其价格发现过程是路径依赖的,某个资产的价格取决于参与者的行为响应。在传统市场以及中心化加密货币交易所,这一点都很明显,即资产价格受到各种因素的影响,比如订单簿深度、买方或卖方流动性、交易历史和私有信息等。
而 CFMM 在很大程度上是 路径独立 的 (假设费用极低) ,这意味着,任何两个数量的价格仅取决于这些数量,而不取决于它们之间的路径。这带来了两个重大好处:
-
因为交易者不管是一次性参与交易,还是一组小型交易,获得的 价格 是一样的,所以他 / 她无需制定如何交易的策略。 -
它提供了一种关于状态的最小表征:我们只需知道 数量 ,就可以为某个资产定价。
CFMM 的弊端
滑点
滑点是指,随着交易者吸收流动性,价格往往会向交易者行为 相反 的方向变化——交易越大,滑点越大。CFMM 会产生较大的 滑点成本 ,因此更适于规模较小的订单。
外部财务风险
向某个 CFMM 添加流动性很简单,但会带来一些复杂的 财务风险 (暂时性亏损、做空波动率、做多波动率 / 金额关联性等) 。
例如,Uniswap 的收益曲线是 凹形 的,这意味着流动性提供者在一定价格区间是盈利的,但在更大的价格变动中会亏钱:
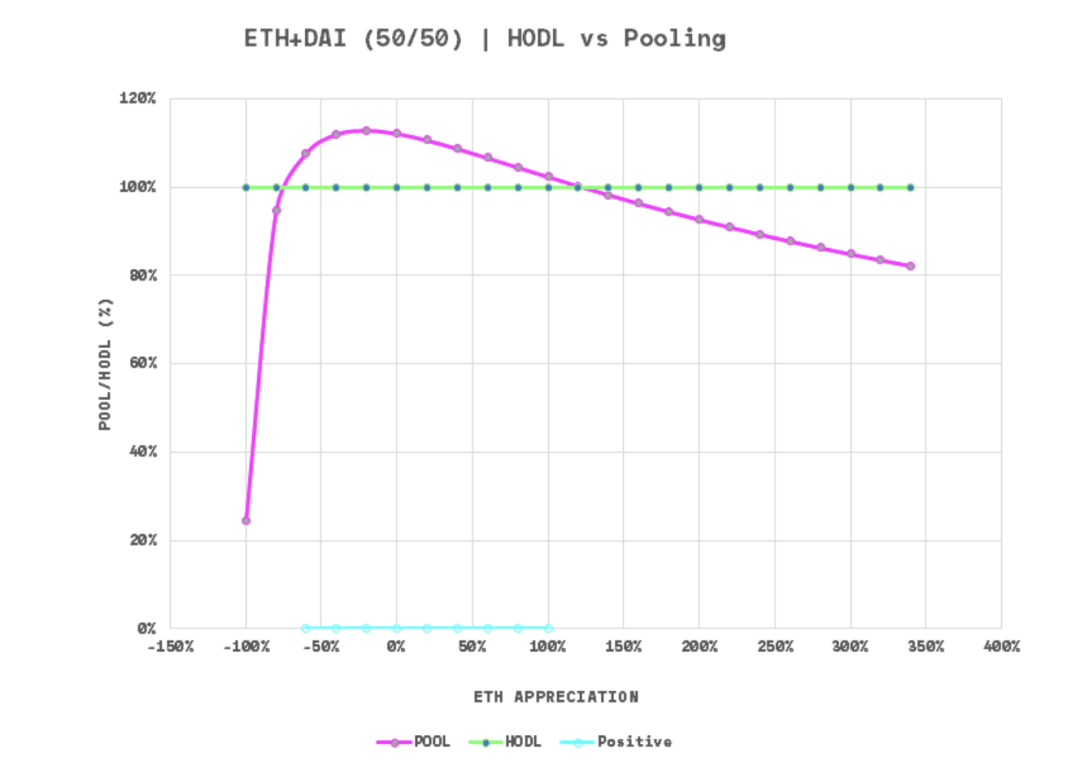
理想情况下,在冒险时我们需要「 凸性 」 (convexity) ,即在风险光谱的两侧都获得正面 (upside) 。这种收益结构的潜台词是,流动性提供者应积极监测资金池中的变化,一旦变化就 迅速行动 ,以防止重大损失。
CFMM 的未来
依资产而定的函数
Curve 和 Shell 已经证明,可以为特定类型的数字资产 量身定制 常数函数 。
因此我相信,除了稳定币,我们还可以针对各种资产类型设计多种多样的 CFMM,比如 衍生品 (例如抵押期权) 和 证券型 代币 (例如房地产) 。
这些 CFMM 的价格函数能最佳的反映各自资产的特征,结果就是滑点的减少和交易效率的提高。
流动性的敏感性
这一属性意味着,做市商应基于市场行为的数量来调整其 定价响应的弹性 。流动性敏感性是值得期待的,因为它从直觉上符合人们对市场起作用的方式的要求:一笔规模固定的投资,在流动性高的市场上的价格变动,应该比在流动性低的市场上要少。
流动性敏感性在当前的 CFMM 中仅限于 价格方面 (比如流动性池越大,价格滑点越小) ,但其他维度也应该可以动态变化。
例如,流动性提供者如果按固定比例收取 交易费 ,那就不是流动性敏感的,因为不论交易额怎么变化,它都是一样的 (比如就是 0.3%,不论流动性池有多大规模) 。
一种替代方法是,在较低的流动性水平上 提高 LP (流动性提供者) 费率 ,以激励 LP 存入其资产 (例如,当低于某个流动性阈值时,费率为 0.5%,高于阈值则为 0.3%) 。
另一种方法是,在市场启动时 降低 LP 费率 ,以此鼓励交易量的增加,当市场成熟时则提高 LP 费率。虽然较低的费率可以增加交易量,但它也可能会挫伤池中流动性。这里有一个有趣的研究领域,即到底什么样的费率能让利润最大化,在交易激励与流动性激励之间保持平衡。
在流动性之外,流动性提供者费率还可以基于其他因素。例如,人们可以基于 尾随波动率 (trailing volatility) 来调整 LP 费率,从而形成一种随机定价机制,并为 CFMM 带来「 波动性敏感性 」这种额外好处。
一级市场
尽管目前大多数的 CFMM 主要用于二级市场的交易,但它们也可以用于引导一级市场的 资产发行 。CFMM 使得发行方能高效地发行实体和数字原生资产,并捕获二级市场的好处,同时改善流动性,为客户改进价格发现。
Unisocks 是这一领域的先锋,它创建了自己的代币,持币人可获得一双 限量版袜子 。Unisocks 创建了 500 个 SOCKS 代币,并将其存入一个有 35 个 ETH 的 Uniswap 流动性池中。如果 ETH 的交易价格为 200 美元,那么第一双袜子的底价则为 14 美元,第 499 双的底价为 350 万美元。Saint Fame 通过销售衬衫使这一概念进一步合法化, Zora 通过创建一个限量版商品的市场来推广该概念,我预计会有更多以类似用例来使用 CFMM 的项目。
有意思的是,这让我们回到了 AMM 的初始用例,即信息诱发,不过,这一次是关于某个资产的价格,而不是某个事件发生的可能性!
总结
常数函数做市商,是金融市场的一项 基础性创新 ,它为自动化做市的学术研究引入了一个激动人心的新领域。
常数函数做市商仍处于发展的萌芽期,我期待着,在未来几年会看到更多新的设计和应用的出现。