社区观点 | 关于MOV巡查官制度的几点思考


在ChainNode白皮书解密读书会01期活动中,比原链高级研究员刘秋杉带领大家领读「MOV:下一代去中心跨链 Layer 2 价值交换协议」白皮书,得到了很多粉丝的关注,其中gentledog的读书帖「关于MOV巡查官制度的几点思考」获得了读书活动的第一名。
正文如下:
根据白皮书,MOV中有巡查官一职防止Bytom侧链作恶。我就在想,这个制度是否存在漏洞呢?经过一番思考,似乎有以下几种攻击方式:
这种攻击是有对策的。有一样东西是作恶者无法复制的:钱包地址!可以采取提案(承诺)+证据的模式,巡查官可以先提交承诺(数据+钱包地址的哈希值),等区块确认后,再公布数据(钱包地址可以不用公布)。这样就能比较完美地解决这个问题了。
先撇开DOS攻击不谈,下面试从经济角度分析巡查官制度。先取一个观察时间段,设在这个观察时间段内,巡查官的巡查成本为U,网关节点的奖励为V,作恶者被举证时遭受的损失为R,作恶成功时获得的收益为S,作恶者作恶的概率为p,巡查官的平均巡查人数为q,某单个巡查官巡查的概率为t。这里假设巡查官的机会是均等的,即当巡查官的巡查人数为q时,成功举证的概率为1/q。则某单个巡查官和作恶者的博弈如下图:

则某单个巡查官的期望支付为
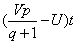
在完全竞争的条件下,某单个巡查官的期望支付应当接近于0。由此可以推算出
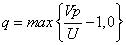
由此可以得知,当
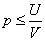
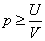
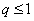
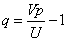
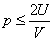
则作恶者的期望收益为
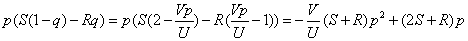
在区间
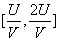
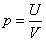
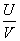
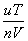
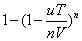
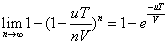
所以,在较长时间段T内,作恶发生的概率为
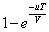
1. 巡查官制度可以减小侧链作恶的概率;
2. 侧链作恶的概率与巡查官的巡查成本U和网关节点的奖励V有关,减小U或增加V都能减小作恶的概率;
3. 侧链作恶的概率与作恶成功时获得的收益S无关,也就是说减少侧链上托管的资产无助于减小作恶的概率;
4. 侧链作恶的概率与作恶者被举证时遭受的损失R无关(如果忽略V≤R的关系),也就是说在不增加网关节点的奖励的前提下,只增加侧链运营者的保证金无助于减小作恶的概率;
5. 由于假装作恶攻击,网关节点的奖励V无法无限增加。巡查官的巡查成本U也无法无限减小。巡查官制度无法杜绝作恶的发生。




